4.15: ASA y AAS
- Page ID
- 107508
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dos juegos de ángulos correspondientes y cualquier conjunto correspondiente de lados demuestran triángulos congruentes.
Postulado de ángulo lateral y teorema de ángulo-ángulo-lado
Si dos ángulos y un lado en un triángulo son congruentes con los dos ángulos correspondientes y un lado en otro triángulo, entonces los dos triángulos son congruentes. Esta idea abarca dos atajos de congruencia triangular: Angle-Side-Angle y Angle-Angle-Side.
Postulado de congruencia de ángulo-lado-ángulo (ASA): Si dos ángulos y el lado incluido en un triángulo son congruentes a dos ángulos y el lado incluido en otro triángulo, entonces los dos triángulos son congruentes.
Teorema de congruencia Angle-Angle-Side (AAS): Si dos ángulos y un lado no incluido en un triángulo son congruentes con dos ángulos y el lado no incluido correspondiente en otro triángulo, entonces los triángulos son congruentes.
La colocación de la palabra Lado es importante porque indica dónde está el lado que se le da en relación con los ángulos. Las imágenes a continuación ayudan a mostrar la diferencia entre los dos atajos.
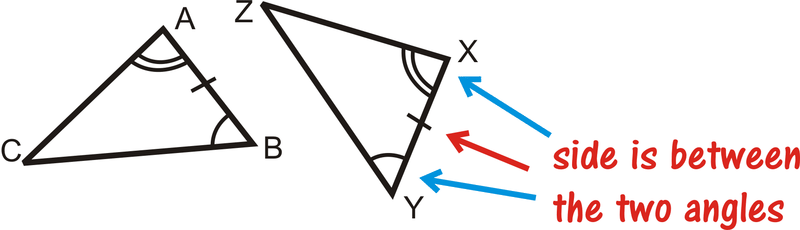
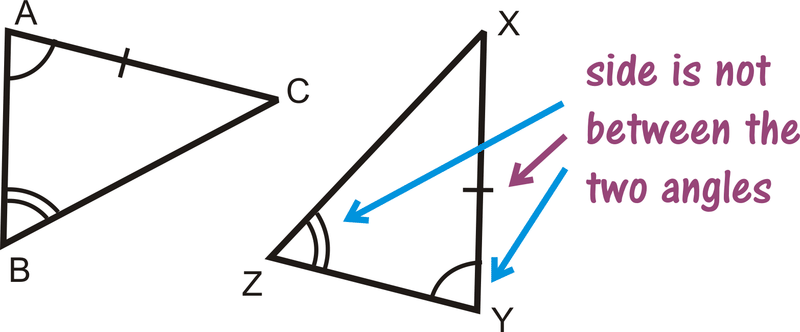
¿Y si te dieran dos triángulos y te proporcionaran solo la medida de dos de sus ángulos y uno de sus longitudes laterales? ¿Cómo podrías determinar si los dos triángulos eran congruentes?
Ejemplo\(\PageIndex{1}\)
¿Se puede probar que los siguientes triángulos son congruentes? ¿Por qué o por qué no?
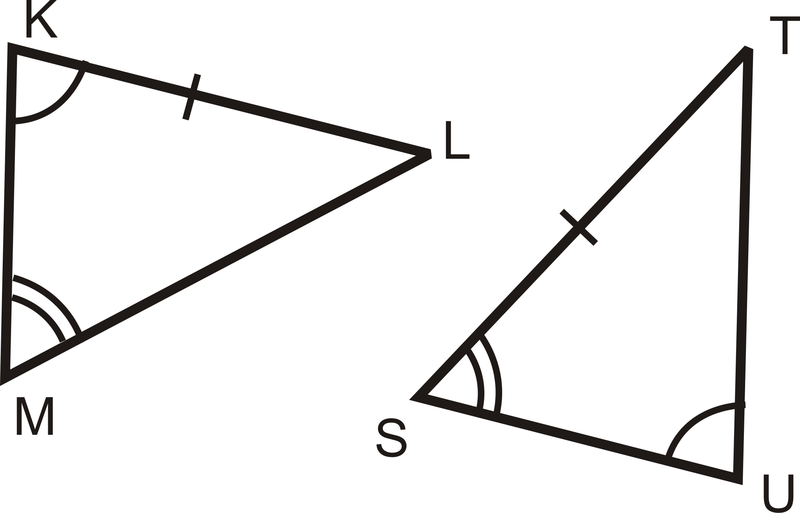
Solución
No podemos demostrar que los triángulos son congruentes porque\(\overline{KL}\) y no\(\overline{ST}\) son correspondientes, aunque sean congruentes. Para determinar si\(\(\overline{KL}\) y\(\overline{ST}\) son correspondientes, mire los ángulos alrededor de ellos,\(\(\angle K\) y\(\angle L\) y\ ángulo S\) y\(\angle T\). \(\angle K\)tiene un arco y\ ángulo L no está marcado. \(\angle S\)tiene dos arcos y no\(\angle T\) está marcado. Para poder utilizar AAS,\(\angle S\) necesita ser congruente con\(\angle K\).
Ejemplo\(\PageIndex{2}\)
Escriba una prueba de 2 columnas.
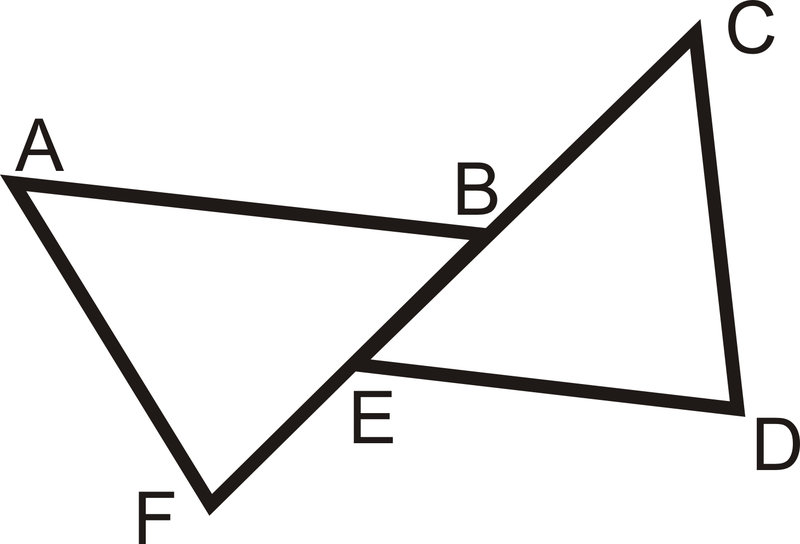
Dado:\(\overline{AB}\parallel \overline{ED}\),\(\angle C\cong \angle F\),\(\overline{AB}\cong \overline{ED}\)
Demostrar:\(\overline{AF}\cong \overline{CD}\)
Solución
| Comunicado | Razón |
|---|---|
| 1. \(\overline{AB}\parallel \overline{ED}\),\(\angle C\cong \angle F\),\(\overline{AB}\cong \overline{ED}\) | 1. Dado |
| 2. \(\angle ABE\cong \angle DEB\) | 2. Teorema de ángulos interiores alternos |
| 3. \(\Delta ABF\cong \Delta DEC\) | 3. ASA |
| 4. \(\overline{AF}\cong \overline{CD}\) | 4. CPCTC (Las Partes Correspondientes de Triángulos Congruentes son Congruentes) |
Ejemplo\(\PageIndex{3}\)
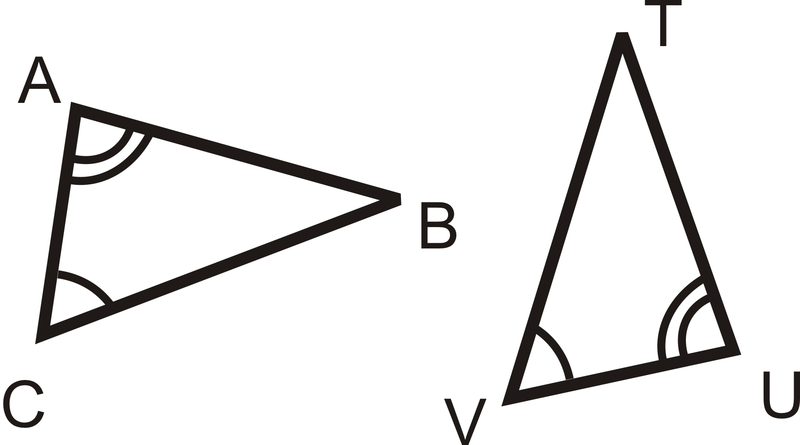
¿Qué información necesitas para probar que estos dos triángulos son congruentes usando el Postulado ASA,\(\overline{AB}\cong UT\overline{AB}\),\(\overline{AC}\cong \overline{UV}\),\(\overline{BC}\cong \overline{TV}\), o\(\angle B\cong \angle T\)?
Solución
Para ASA, necesitamos el lado entre los dos ángulos dados, que es\(\overline{AC}\) y\(\overline{UV}\). La respuesta es\(\overline{AC}\cong \overline{UV}\).
Ejemplo\(\PageIndex{4}\)
Escriba una prueba de 2 columnas.
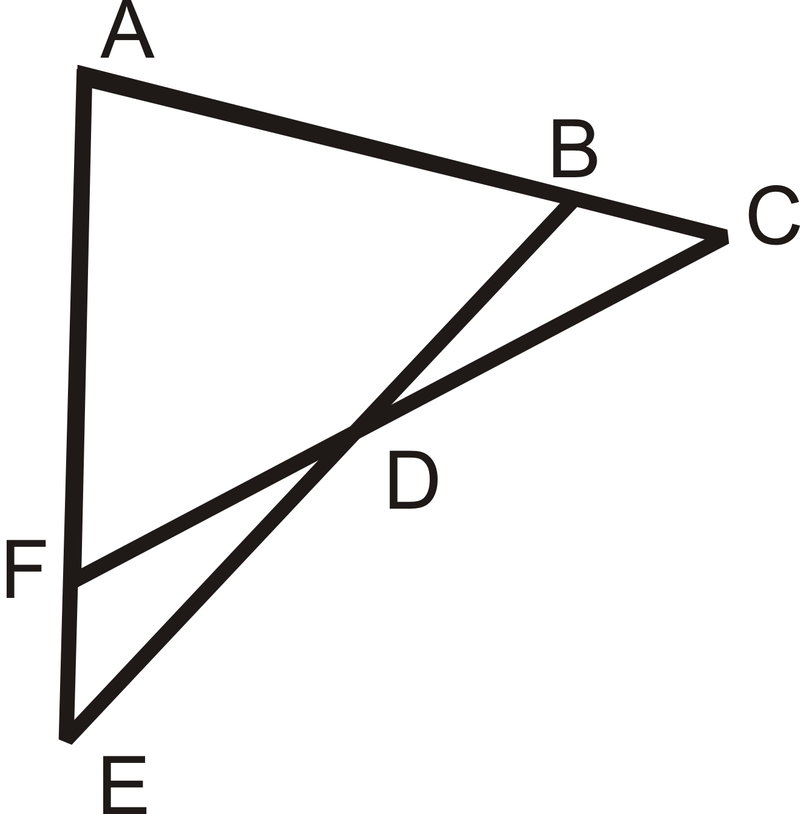
Dado:\(\angle C\cong \angle E\),\(\overline{AC}\cong \overline{AE}\)
Demostrar:\(\Delta ACF\cong \Delta AEB \)
Solución
| Comunicado | Razón |
|---|---|
| 1. \(\angle C\cong \angle E\),\(\overline{AC}\cong \overline{AE}\) | 1. Dado |
| 2. \(\angle A\cong \angle A\) | 2. reflexivo\(PoC\) |
| 3. \(\Delta ACF \cong \Delta AEB\) | 3. ASA |
Ejemplo\(\PageIndex{5}\)
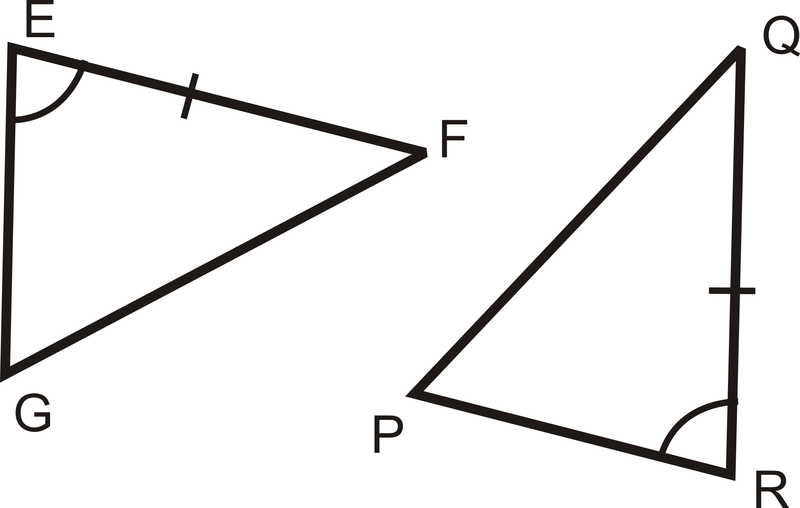
¿Qué información necesitas para probar que estos dos triángulos son congruentes usando ASA? AAS?
Solución
Para ASA, necesitamos los ángulos del otro lado de\(\overline{EF}\) y\(\overline{QR}\). \(\angle F\cong \angle Q\)
Para AAS, necesitaríamos el otro ángulo. \(\angle G\cong \angle P\)
Revisar
Para las preguntas 1-3, determinar si los triángulos son congruentes. Si lo son, escribe la declaración de congruencia y qué congruencia postula o teorema utilizaste.
-
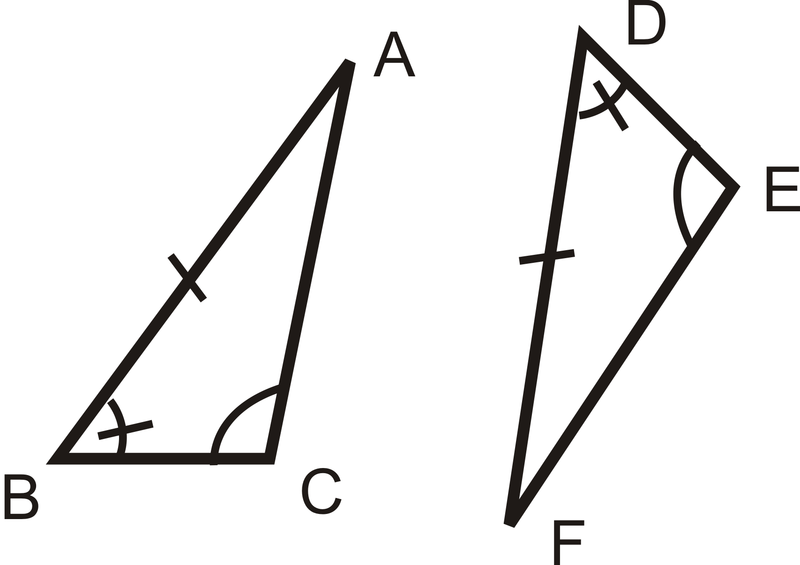
Figura\(\PageIndex{8}\) -
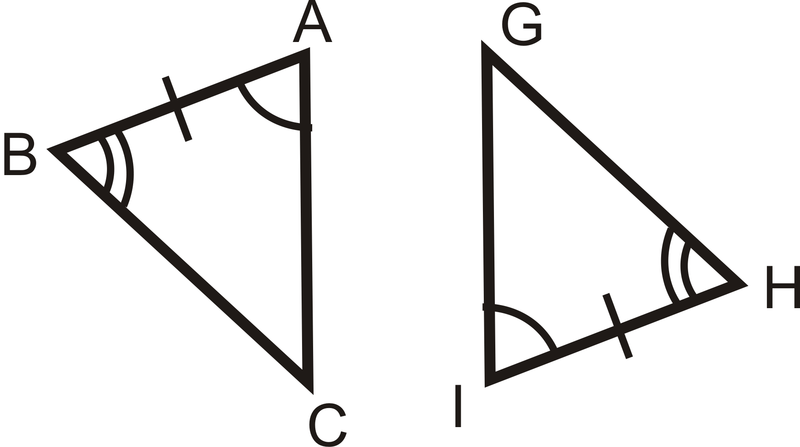
Figura\(\PageIndex{9}\) -
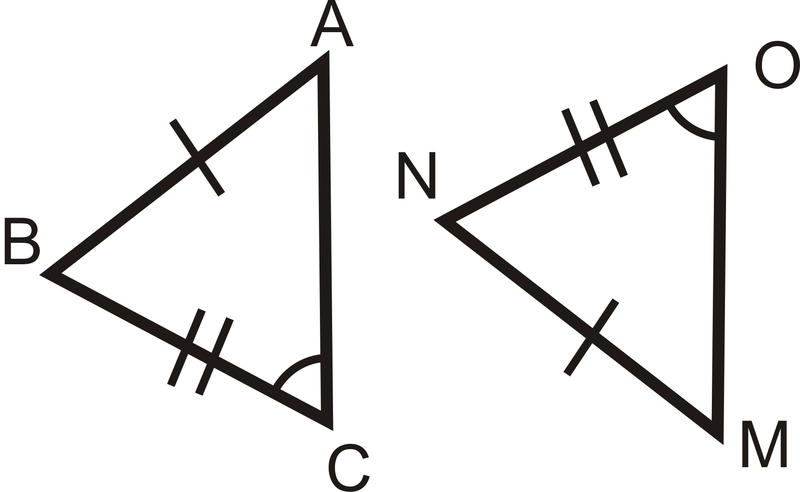
Figura\(\PageIndex{10}\)
Para las preguntas 4-8, use la imagen y la información dada a continuación.
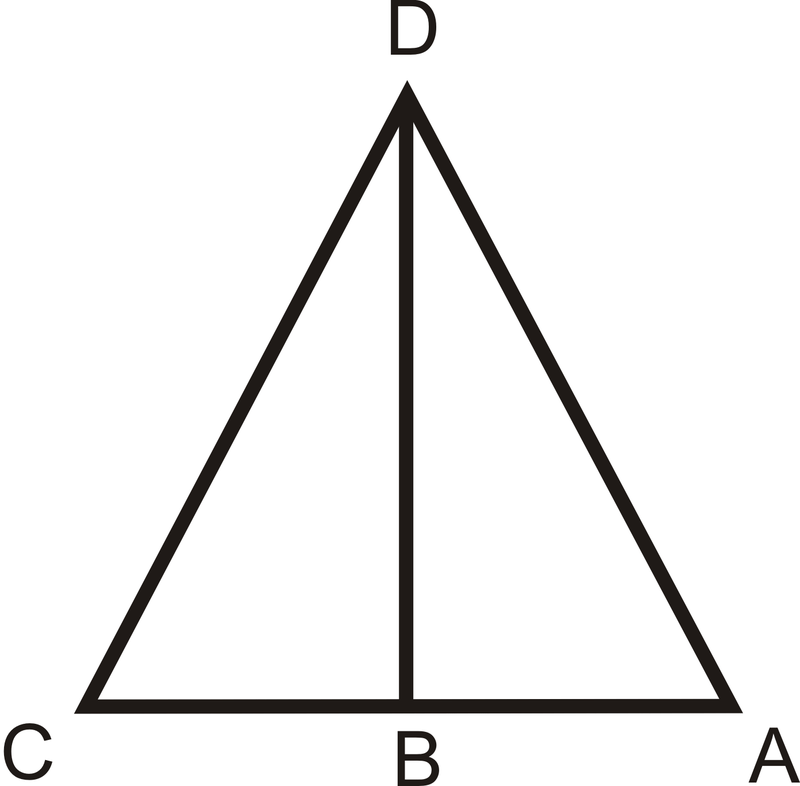
Dado:\(\overline{DB}\perp \overline{AC}\),\(\overline{DB}\) es el ángulo bisectriz de\(\angle CDA\)
- De\(\overline{DB}\perp \overline{AC}\), ¿qué ángulos son congruentes y por qué?
- Porque\(\overline{DB}\) es el ángulo bisectriz de\(\angle CDA\), ¿qué dos ángulos son congruentes?
- De mirar la imagen, ¿qué dato adicional se le da? ¿Esto es suficiente para probar que los dos triángulos son congruentes?
- Escriba un comprobante de 2 columnas para probarlo\(\Delta CDB\cong \Delta ADB\), usando #4 -6.
- ¿Cuál sería tu razón\(\angle C\cong \angle A\)?
Para las preguntas 9-13, use la imagen y la información dada.
Dado:\(\overline{LP}\parallel \overline{NO}\),\(\overline{LP}\cong \overline{NO}\)
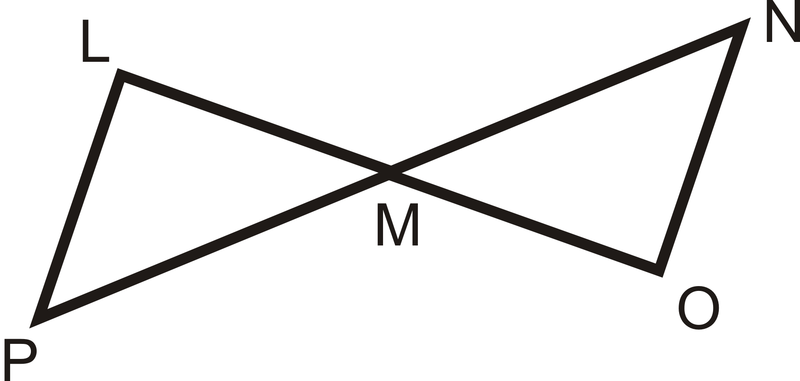
- De\(\overline{LP}\parallel \overline{NO}\), ¿qué ángulos son congruentes y por qué?
- De mirar la imagen, ¿qué dato adicional se puede concluir?
- Escriba un comprobante de 2 columnas para probarlo\(\Delta LMP\cong \Delta OMN\).
- ¿Cuál sería tu razón\(\overline{LM}\cong \overline{MO}\)?
- Rellene los espacios en blanco para la prueba a continuación. Utilice lo dado desde arriba. Demostrar:\(M\) es el punto medio de\(\overline{PN}\).
| Comunicado | Razón |
|---|---|
| 1. \(\overline{LP}\parallel \overline{NO}\),\(\overline{LP}\cong \overline{NO}\) | 1. Dado |
| 2. | 2. Ángulos interiores alternos |
| 3. | 3. ASA |
| 4. \(\overline{LM}\cong \overline{MO}\) | 4. |
| 5. \(M\)es el punto medio de\(\overline{PN}\). | 5. |
Determinar la información adicional necesaria para mostrar que los dos triángulos son congruentes por el postulado dado.
- AAS
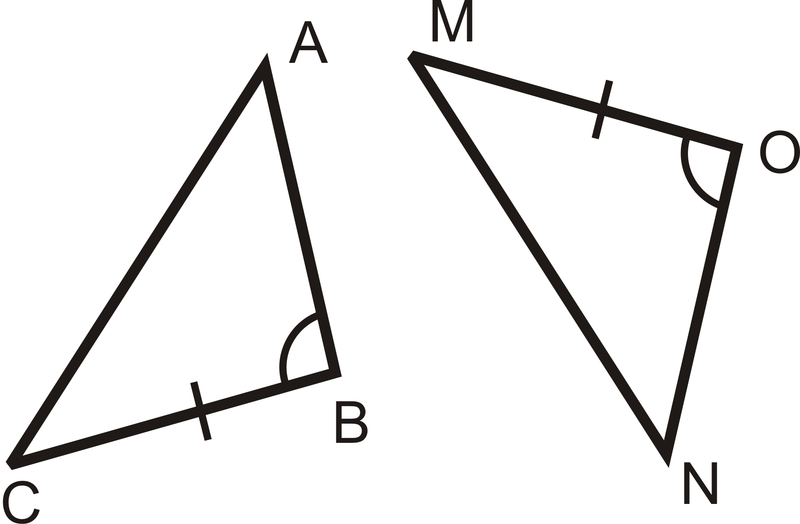
Figura\(\PageIndex{13}\) - ASA

Figura\(\PageIndex{14}\) - ASA
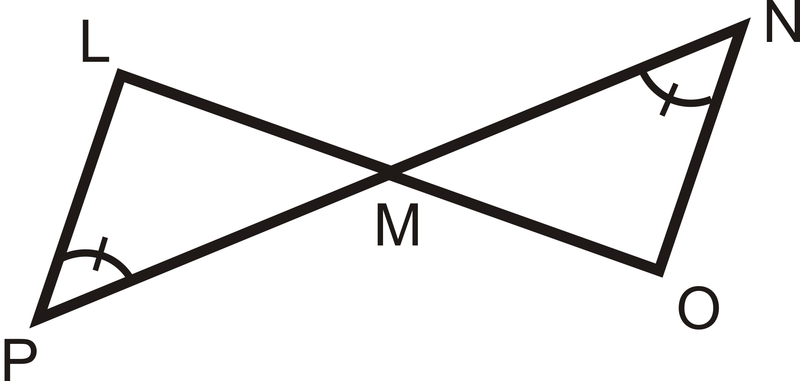
Figura\(\PageIndex{15}\) - AAS

Figura\(\PageIndex{16}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.8.
Recursos
vocabulario
| Término | Definición |
|---|---|
| CPCTC | Las Partes Correspondientes de Triángulos Congruentes son Congruentes. Se utiliza para mostrar que dos lados o dos ángulos en triángulos son congruentes después de haber demostrado que los triángulos son congruentes. |
| AAS (Angle-Angle-Side) | Si dos ángulos y un lado no incluido en un triángulo son congruentes con dos ángulos y el lado no incluido correspondiente en otro triángulo, entonces los triángulos son congruentes. |
| Ángulo Ángulo Lateral Triángulo | El término 'triángulo ángulo-lado-ángulo' se refiere a un triángulo con medidas conocidas de dos ángulos y la longitud del lado entre ellos. |
| ASA | ASA, ángulo-lado-ángulo, se refiere a dos ángulos conocidos en un triángulo con un lado conocido entre los ángulos conocidos. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Congruencia del Triángulo | La congruencia del triángulo ocurre si 3 lados en un triángulo son congruentes a 3 lados en otro triángulo. |
| Transformación Rígida | Una transformación rígida es una transformación que conserva la distancia y los ángulos, no cambia el tamaño ni la forma de la figura. |
Recursos adicionales
Video: Introducción a los triángulos congruentes
Actividades: ASA y AAS Triángulo Congruencia Discusión Preguntas
Ayudas de estudio: Guía de estudio de congruencia triangular
Práctica: ASA y AAS
Mundo Real: Congruencia del Triángulo SSS

