4.25: Comparando ángulos y lados en triángulos
- Page ID
- 107520
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Teoremas de desigualdad y ángulos de ordenamiento y lados de triángulos.
Teoremas de Desigualdad SAS y SSS
Mira el triángulo de abajo. Se dan los lados del triángulo. ¿Se puede determinar qué ángulo es el más grande? El ángulo más grande será opuesto al 18 porque ese es el lado más largo. De igual manera, el ángulo más pequeño será opuesto al 7, que es el lado más corto.
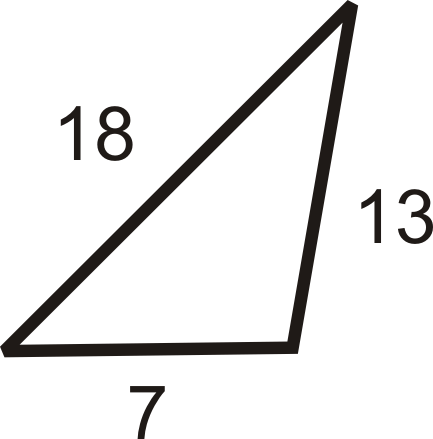
Esta idea es en realidad un teorema: Si un lado de un triángulo es más largo que otro lado, entonces el ángulo opuesto al lado más largo será mayor que el ángulo opuesto al lado más corto.
Lo contrario también es cierto: Si un ángulo en un triángulo es mayor que otro ángulo en ese triángulo, entonces el lado opuesto al ángulo mayor será más largo que el lado opuesto al ángulo más pequeño.
Podemos extender esta idea en dos teoremas que nos ayuden a comparar lados y ángulos en dos triángulos Si tenemos dos triángulos congruentes\(\Delta ABC\) y\(\Delta DEF\), marcados a continuación:
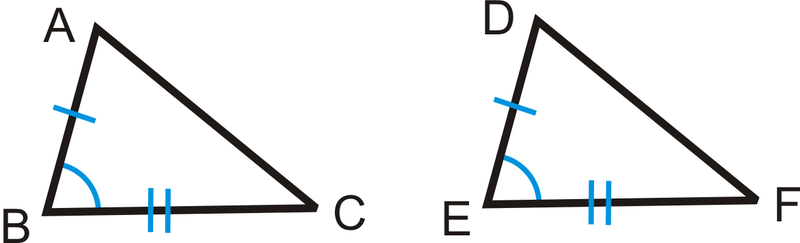
Por lo tanto\(AB=DE\), si\(BC=EF\),, y\(m\angle B=m\angle E\), entonces\(AC=DF\).
Ahora, vamos a hacer\(m\angle B>m\angle E\). ¿Eso haría\(AC>DF\)? Sí. Esta idea se llama Teorema de Desigualdad SAS.
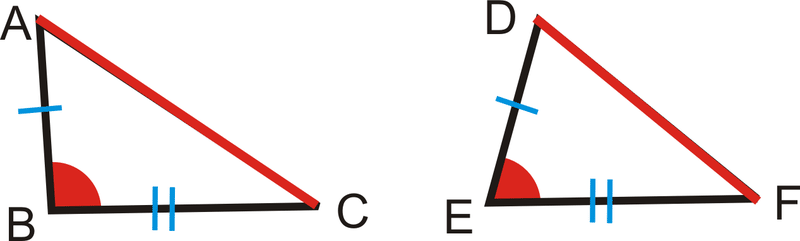
El Teorema de Desigualdad SAS: Si dos lados de un triángulo son congruentes con dos lados de otro triángulo, pero el ángulo incluido de un triángulo tiene mayor medida que el ángulo incluido del otro triángulo, entonces el tercer lado del primer triángulo es más largo que el tercer lado del segundo triángulo.

Si\(\overline{AB}\cong \overline{DE}\),\(\overline{BC}\cong \overline{EF}\) y\(m\angle B>m\angle E\), entonces\(\overline{AC}>\overline{DF}\).
Si conocemos los terceros lados en contraposición a los ángulos, la idea opuesta también es cierta y se llama Teorema de Desigualdad SSS.
Teorema de Desigualdad SSS: Si dos lados de un triángulo son congruentes con dos lados de otro triángulo, pero el tercer lado del primer triángulo es más largo que el tercer lado del segundo triángulo, entonces el ángulo incluido de los dos lados congruentes del primer triángulo es mayor en medida que el incluyó el ángulo de los dos lados congruentes del segundo triángulo.

Si\(\overline{AB}\cong \overline{DE}\),\(\overline{BC}\cong \overline{EF}\) y\(\overline{AC}>\overline{DF}\), entonces\( m\angle B>m\angle E\).
¿Y si te dijeran que un triángulo tiene lados que miden 3, 4 y 5? ¿Cómo podrías determinar cuál de los ángulos del triángulo es el más grande? ¿El más pequeño?
Ejemplo\(\PageIndex{1}\)
Si\(\overline{XM}\) es una mediana de\(\Delta XYZ\) y\(XY>XZ\), ¿qué podemos decir sobre\(m\angle 1\) y\(m\angle 2\)?
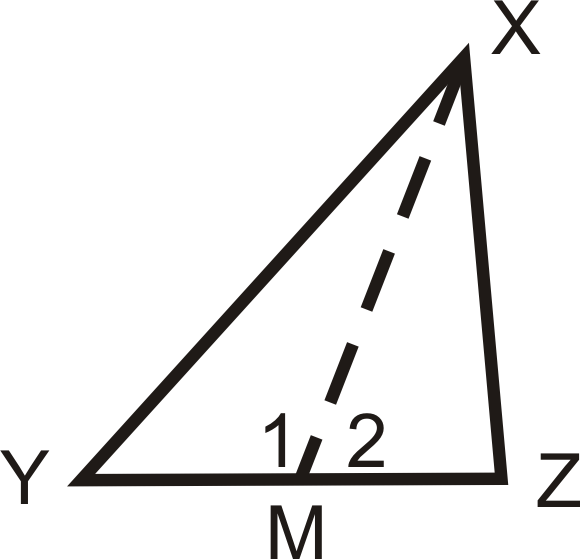
Solución
M es el punto medio de\(\overline{YZ}\), entonces\(YM=MZ\). \(MX=MX\)por la Propiedad Reflexiva y sabemos\(XY>XZ\).
Podemos usar el Teorema de Desigualdad de SSS Converse para decir\(m\angle 1>m\angle 2\).
Ejemplo\(\PageIndex{2}\)
A continuación se muestra el triángulo isósceles\(\Delta ABC\). Enumere todo lo que pueda sobre los lados y ángulos del triángulo y por qué.
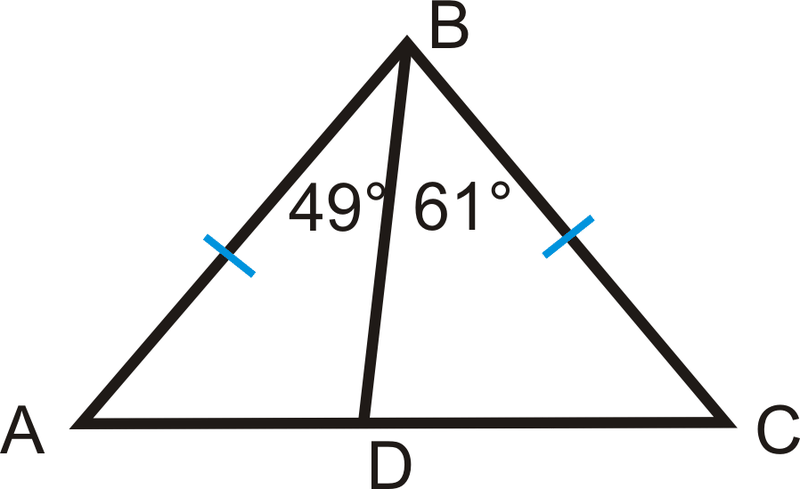
Solución
M es el punto medio de\(\overline{YZ}\), entonces\(YM=MZ\). \(MX=MX\)por la Propiedad Reflexiva y sabemos\(XY>XZ\).
\(AB=BC\)porque se da.
\(m\angle A=m\angle C\)porque si los lados son iguales que sus ángulos opuestos deben ser iguales..
\(AD<DC\)porque\(m\angle ABD<m\angle CBD\) y por el Teorema de Desigualdad del Triángulo SAS.
Ejemplo\(\PageIndex{3}\)
Enumere los lados en orden, del más corto al más largo.
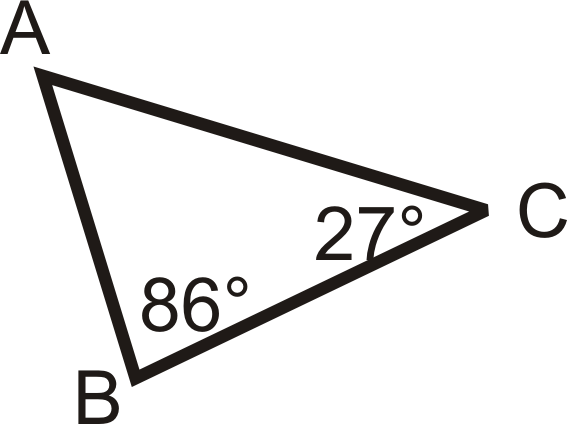
Solución
Primero, encuentra m\ ángulo A. Del Teorema de la Suma del Triángulo:
\(\begin{align*} m\angle A+86^{\circ}+27^{\circ}&=180^{\circ} \\ m\angle A&=67^{\circ} \end{align*}\)
\(86^{\circ}\)es el ángulo más grande, así\(AC\) es el lado más largo. El siguiente ángulo es\(67^{\circ}\), así\(BC\) sería el siguiente lado más largo. \(27^{\circ}\)es el ángulo más pequeño, así\(AB\) es el lado más corto. En orden, la respuesta es:\(AB\),\(BC\),\(AC\).
Ejemplo\(\PageIndex{4}\)
Enumere los ángulos en orden, de mayor a menor.
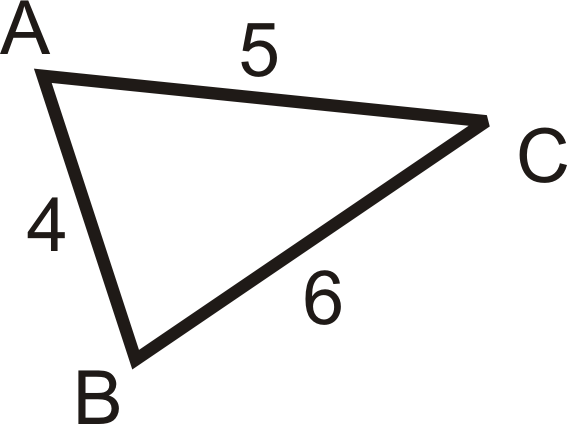
Solución
Al igual que con los lados, el ángulo más grande es opuesto al lado más largo. El lado más largo es\(BC\), por lo que el ángulo más grande es\(\angle A\). Lo siguiente sería\(\angle B\) y luego\(\angle C\).
Ejemplo\(\PageIndex{5}\)
Listar los lados en orden, de menor a mayor.
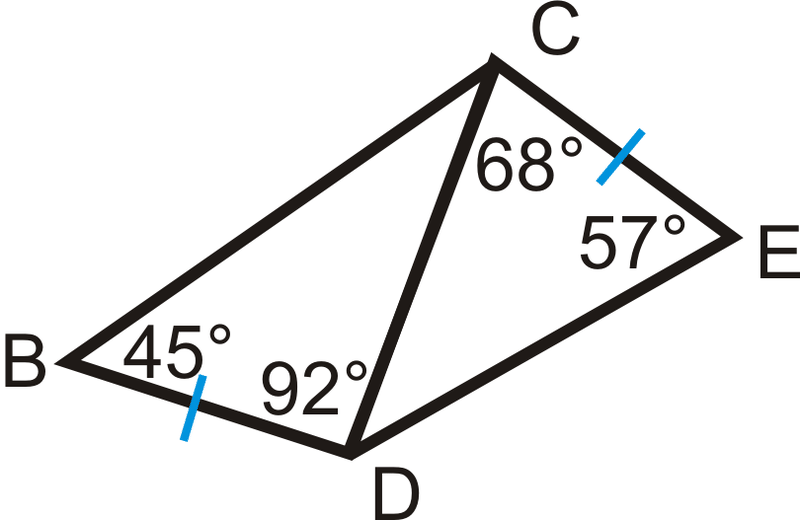
Solución
Para resolver, comencemos con\ Delta DCE\). El ángulo que falta es\(55^{\circ}\). Por el teorema presentado en esta sección, los lados, en orden de menor a mayor son\(CE\),\(CD\), y\(DE\).
Para\(\Delta BCD\), el ángulo que falta es\(43^{\circ}\). Nuevamente, por el teorema presentado en esta sección, el orden de los lados de menor a mayor es\(BD\),\(CD\), y\(BC\).
Por el Teorema de Desigualdad SAS, lo sabemos\(BC>DE\), así que el orden de todas las partes sería:\(BD\),\(CE\),,\(CD\),\(DE\),\(BC\).
Revisar
Para las preguntas 1-3, enumere los lados en orden del más corto al más largo.
-
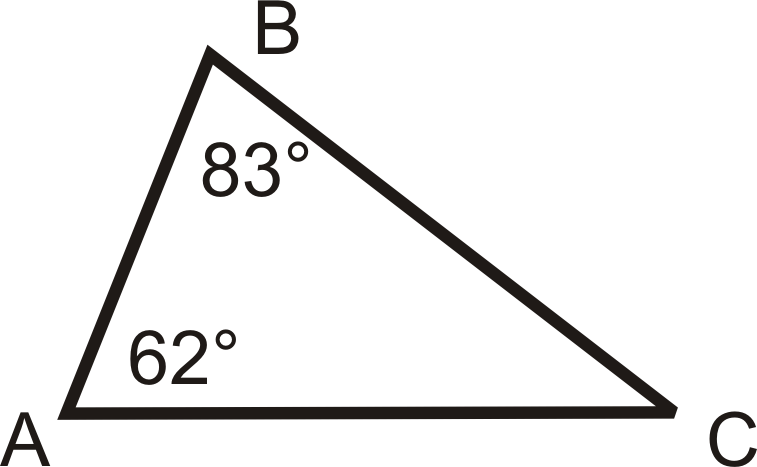
Figura\(\PageIndex{11}\) -
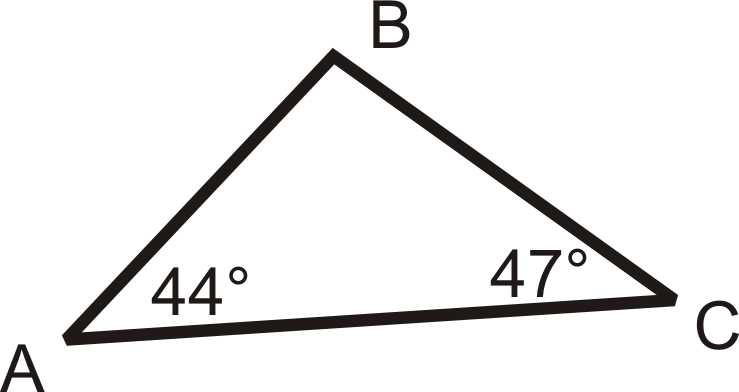
Figura\(\PageIndex{12}\) -
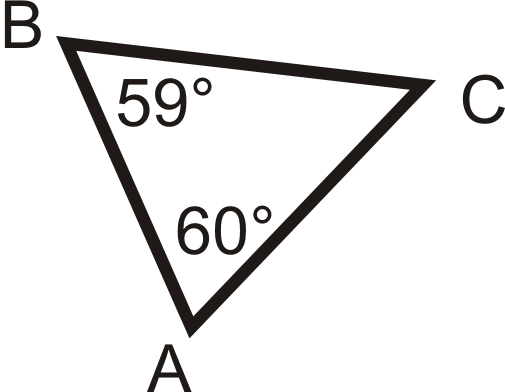
Figura\(\PageIndex{13}\)
Para las preguntas 4-6, enumere los ángulos de mayor a menor.
-
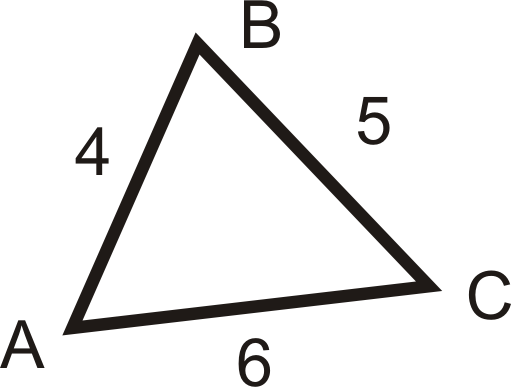
Figura\(\PageIndex{14}\) -
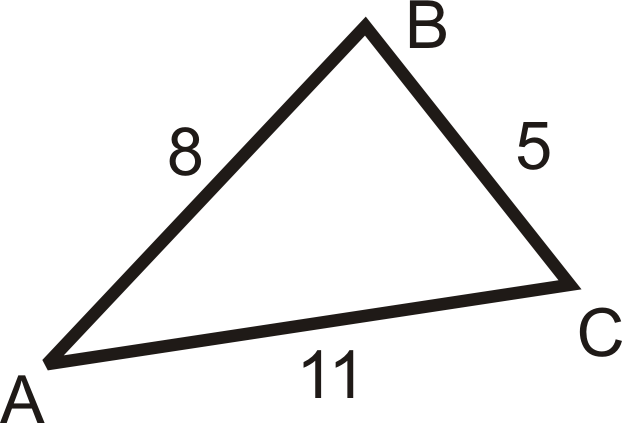
Figura\(\PageIndex{15}\) -
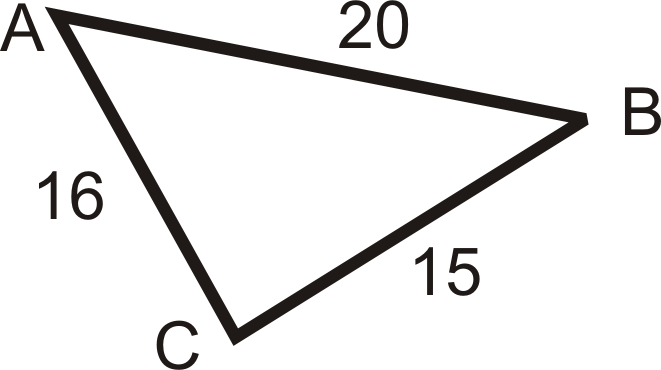
Figura\(\PageIndex{16}\) - Dibuja un triángulo con lados de 3 cm, 4 cm y 5 cm. Las medidas del ángulo son\(90^{\circ}\),\(53^{\circ}\), y\(37^{\circ}\). Coloque las medidas de ángulo en los puntos apropiados.
- Dibuja un triángulo con medidas de ángulo\(56^{\circ}\),\(54^{\circ}\) y el lado incluido es de 8 cm. ¿Cuál es el lado más largo de este triángulo?
- Dibuja un triángulo con lados de 6 cm, 7 cm y 8 cm. Las medidas del ángulo son\(75.5^{\circ}\),\(58^{\circ}\), y\(46.5^{\circ}\). Coloque las medidas de ángulo en los puntos apropiados.
- ¿Qué conclusiones puedes sacar\(x\)?
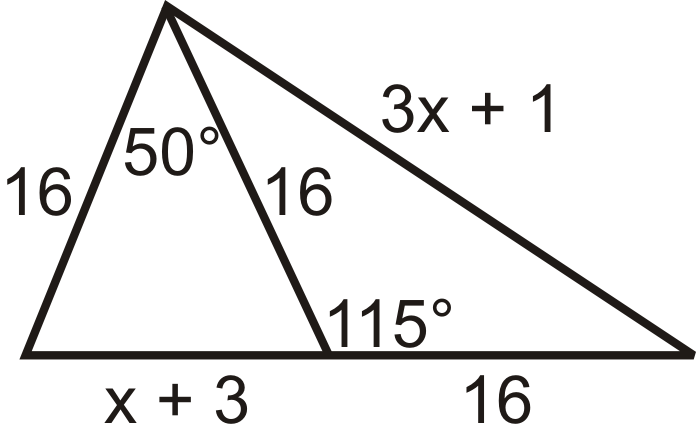
Figura\(\PageIndex{17}\) - Comparar\(m\angle 1\) y\(m\angle 2\).
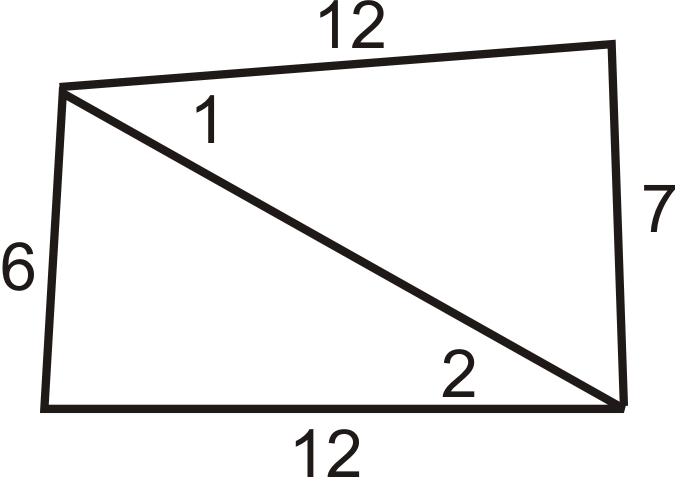
Figura\(\PageIndex{18}\) - Enumere los lados del más corto al más largo.
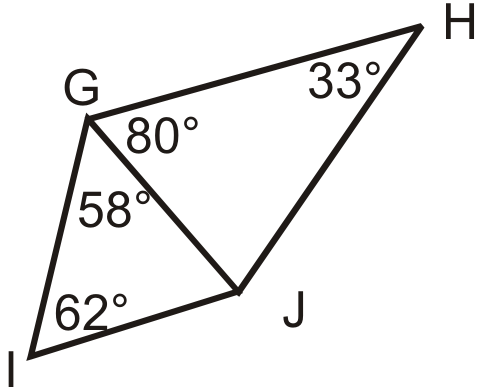
Figura\(\PageIndex{19}\) - Comparar\(m\angle 1\) y\(m\angle 2\). ¿Qué puedes decir sobre\(m\angle 3\) y\(m\angle 4\)?
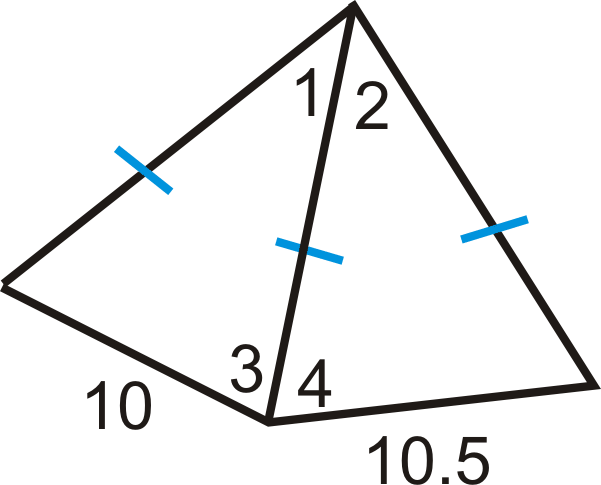
Figura\(\PageIndex{20}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.6.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Teorema de desigualdad SAS | El Teorema de Desigualdad SAS establece que si dos lados de un triángulo son congruentes con dos lados de otro triángulo, pero el ángulo incluido de un triángulo tiene mayor medida que el ángulo incluido del otro triángulo, entonces el tercer lado del primer triángulo es más largo que el tercer lado del segundo triángulo . |
| Teorema de Desigualdad SSS | El Teorema de Desigualdad SSS establece que si dos lados de un triángulo son congruentes con dos lados de otro triángulo, pero el tercer lado del primer triángulo es más largo que el tercer lado del segundo triángulo, entonces el ángulo incluido de los dos lados congruentes del primer triángulo es mayor en medida que el incluyó el ángulo de los dos lados congruentes del segundo triángulo. |
| Teorema de suma de triángulo | El Teorema de la Suma del Triángulo establece que los tres ángulos interiores de cualquier triángulo suman 180 grados. |
Recursos adicionales
Elemento Interactivo
Video: Comparación de ángulos y lados en triángulos Principios - Básico
Actividades: Comparando ángulos y lados en triángulos
Ayudas de estudio: Guía de estudio de desigualdades en triángulos
Práctica: Comparar ángulos y lados en triángulos
Mundo real: Teorema de la suma del triángulo

