4.24: Altitudes
- Page ID
- 107571
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Altura de un triángulo o del segmento de línea desde un vértice y perpendicular al lado opuesto.
En un triángulo, un segmento de línea desde un vértice y perpendicular al lado opuesto se denomina altitud. También se le llama la altura de un triángulo. Las líneas rojas de abajo son todas las altitudes.
Cuando un triángulo es un triángulo rectángulo, la altitud, o altura, es la pierna. Si el triángulo es obtuso, entonces la altitud estará fuera del triángulo. Si el triángulo es agudo, entonces la altitud estará dentro del triángulo.
¿Y si te dieran una o más medidas de ángulo de un triángulo? ¿Cómo determinaría dónde se encontraría la altitud del triángulo?
Ejemplo\(\PageIndex{1}\)
Verdadero o falso: Las altitudes de un triángulo obtuso están dentro del triángulo.
Solución
Cada triángulo tiene tres altitudes. Para un triángulo obtuso, al menos una de las altitudes estará fuera del triángulo, como se muestra en la imagen al inicio de esta sección.
Ejemplo\(\PageIndex{2}\)
Dibuja la altitud para el triángulo mostrado.
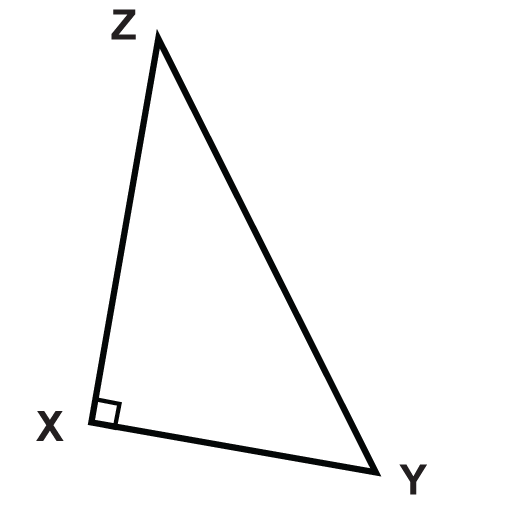
Solución
El triángulo es un triángulo rectángulo, por lo que la altitud ya está dibujada. La altitud es\(\overline{XZ}\).
Ejemplo\(\PageIndex{3}\)
¿De qué segmento de línea es la altitud\(\Delta ABC\)?
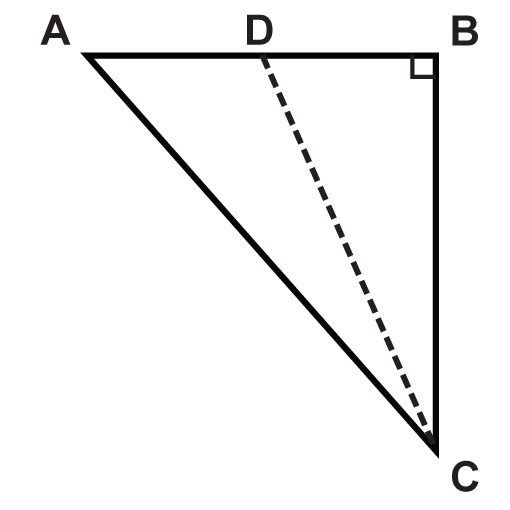
Solución
En un triángulo rectángulo, la altitud, o la altura, es la pierna. Si giramos el triángulo para que el ángulo recto esté en la esquina inferior izquierda, vemos que la pierna\(\overline{BC}\) es la altitud.
Ejemplo\(\PageIndex{4}\)
Un triángulo tiene ángulos que miden\(55^{\circ}\),\(60^{\circ}\), y\(65^{\circ}\). ¿Dónde se encontrará la altitud?
Solución
Debido a que todas las medidas de ángulo son menores que\(90^{\circ}\), el triángulo es un triángulo agudo. La altitud de cualquier triángulo agudo está dentro del triángulo.
Ejemplo\(\PageIndex{5}\)
Un triángulo tiene un ángulo que mide\(95^{\circ}\). ¿Dónde se encontrará una altitud?
Solución
Porque\(95^{\circ}>90^{\circ}\), el triángulo es obtuso y estará fuera del triángulo.
Revisar
Dados los siguientes triángulos, diga si la altitud está dentro del triángulo, fuera del triángulo, o en la pierna del triángulo.
-
Figura\(\PageIndex{4}\) -
Figura\(\PageIndex{5}\) -
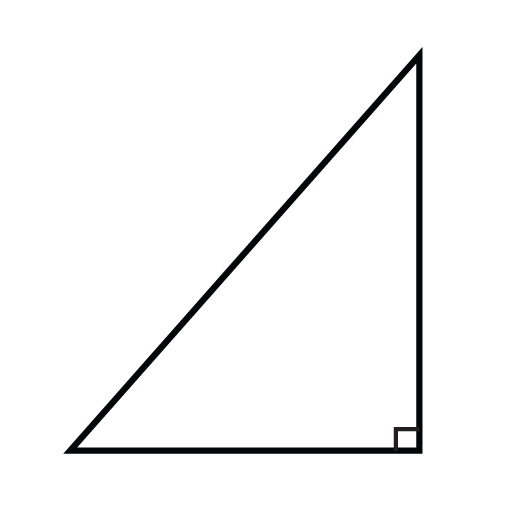
Figura\(\PageIndex{6}\) -
Figura\(\PageIndex{7}\) -
Figura\(\PageIndex{8}\) - \(\Delta JKL\)es un triángulo equiangular.
- \(\Delta MNO\)es un triángulo en el que dos los ángulos miden\(30^{\circ}\) y\(60^{\circ}\).
- \(\Delta PQR\)es un triángulo isósceles en el que dos de los ángulos miden\(25^{\circ}\).
- \(\Delta STU\)es un triángulo isósceles en el que miden dos ángulos\(45^{\circ}\).
Dados los siguientes triángulos, ¿qué segmento de línea es la altitud?
- \(\Delta ABC \)
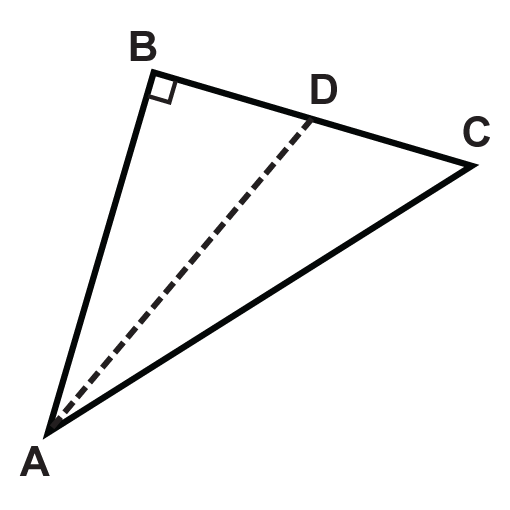
Figura\(\PageIndex{9}\) - \(\Delta EGH \)
Figura\(\PageIndex{10}\) - \(\Delta IJK \)
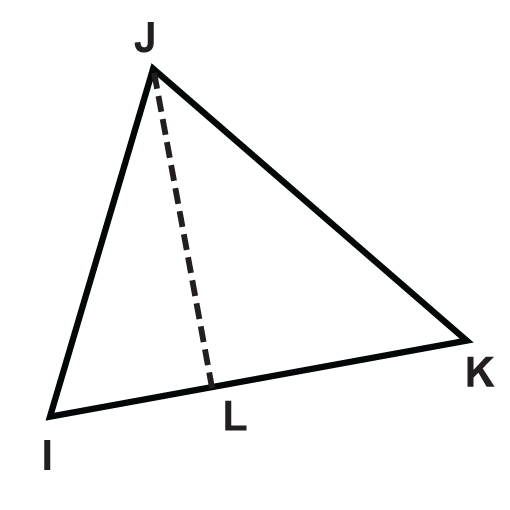
Figura\(\PageIndex{11}\) - \(\Delta MNO \)
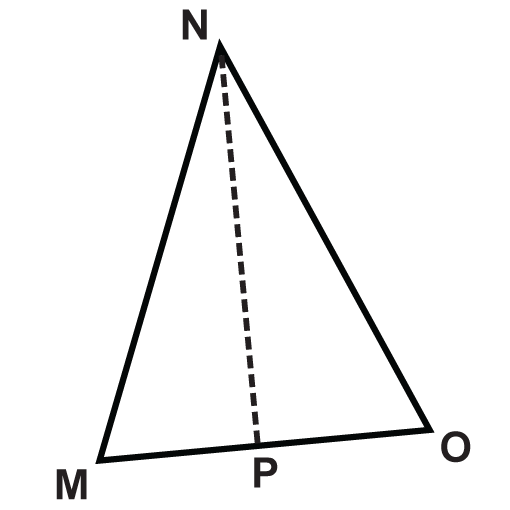
Figura\(\PageIndex{12}\) - \(\Delta RSQ \)
Figura\(\PageIndex{13}\) - \(\Delta UVW \)
Figura\(\PageIndex{14}\)
Recursos
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.5.
El vocabulario
| Término | Definición |
|---|---|
| altitud | Una altitud de un triángulo es un segmento de línea desde un vértice y es perpendicular al lado opuesto. También se le llama la altura de un triángulo. |
Recursos adicionales
Elemento Interactivo
Video: Principios de Altitud - Básico
Actividades: Altitudes Preguntas de Discusión
Ayudas de Estudio: Bisectores, Medianos, Altitudes Guía de Estudio
Mundo Real: Altitudes