4.32: Aplicaciones del Teorema de Pitágoras

Descubrir, probar geométricamente y aplicar el Teorema de Pitágoras.

Longitudes de lados triangulares usando el teorema de Pitágoras

Acabas de inscribirte para ser asistente de arquitecto en una nueva oficina en el centro. Se le pide que dibuje un modelo a escala de una escultura para una plaza de negocios. La escultura tiene una gran pieza triangular donde uno de los ángulos entre los lados es de noventa grados. Este tipo de triángulo se llama “triángulo rectángulo”. El arquitecto para el que trabajas entra a la habitación y te dice que los lados del triángulo que forman el ángulo recto son de 9 pies y 12 pies. ¿Se puede decir cuánto dura el tercer lado?

Encontrar la longitud de los lados del triángulo usando el teorema de Pitágoras

De Geometría, recordemos que el Teorema de Pitágoras es\(a^2+b^2=c^2\) donde\(a\) y\(b\) son las patas de un triángulo rectángulo y c es la hipotenusa. Además, el lado opuesto al ángulo es minúscula y el ángulo es mayúscula. Por ejemplo, el ángulo\(A\) es lado opuesto\(a\).

Figura\(\PageIndex{1}\)

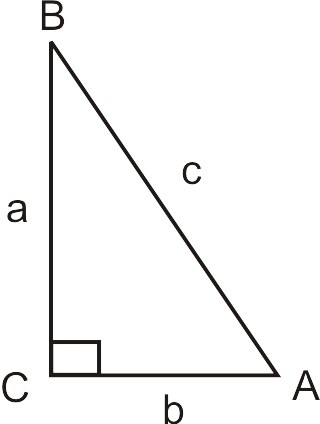
El Teorema de Pitágoras se utiliza para resolver los lados de un triángulo rectángulo.

Usando el Teorema de Pitágoras

1.

Figura\(\PageIndex{2}\)

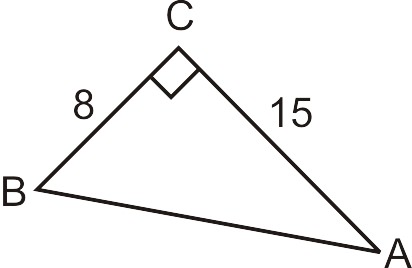
\(a=8\),\(b=15\), necesitamos encontrar la hipotenusa.

\(\begin{align*} 82+152 &= c^2 \\ 64+225 &= c^2 \\ 289 &= c^2 \\ 17 &= c\end{align*}\)

Observe, no incluimos -17 como solución porque un número negativo no puede ser un lado de un triángulo.

2.

Figura\(\PageIndex{3}\)

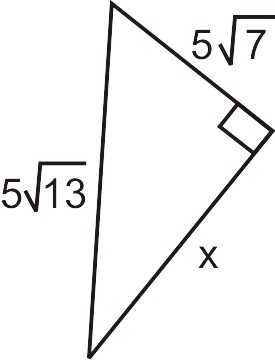
Usa el Teorema de Pitágoras para encontrar la pierna faltante.

\(\begin{align*}(5\sqrt{7})^2+x^2 &= (5\sqrt{13})^2 \\ 25\cdot 7+x^2 &= 25\cdot 13 \\ 175+x^2 &= 325 \\ x^2 &= 150 \\ x &= 5\sqrt{6}\end{align*}\)

Figura\(\PageIndex{4}\)

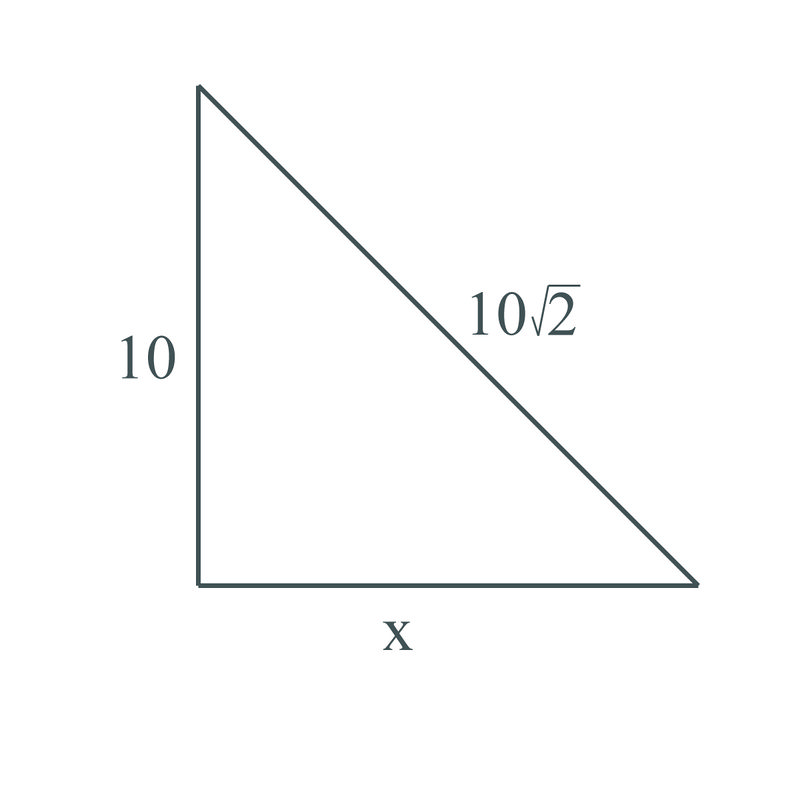
3. Usa el Teorema de Pitágoras para encontrar la pierna faltante en el triángulo de arriba.

\(\begin{align*}10^2+x^2 &= (10\sqrt{2})^2 \\ 100+x^2 &= 100\cdot 2 \\ 100+x^2 &= 100 \\ x^2 &= 100 \\ x &= 10\end{align*}\)

Ejemplo\(\PageIndex{1}\)

Antes, te dieron un problema pidiéndote que dibujaras una maqueta a escala de una escultura para una plaza de negocios.

Solución

Con tu conocimiento del Teorema de Pitágoras, puedes ver que el triángulo tiene lados con longitudes de 9 pies y 12 pies. Trabajas para encontrar la hipotenusa:

\(\begin{align*} a^2+b^2 &= c^2 \\ 9^2+12^2 &= c^2 \\ 81+144 &= c^2 \\ 225 &= c^2 \\ (\sqrt{225}) &= 15=c\end{align*}\)

Con el conocimiento de que la longitud del tercer lado del triángulo es de 15 pies, puedes construir tu maqueta con facilidad.

Ejemplo\(\PageIndex{2}\)

Usa el Teorema de Pitágoras para encontrar el lado faltante del siguiente triángulo:

Figura\(\PageIndex{5}\)

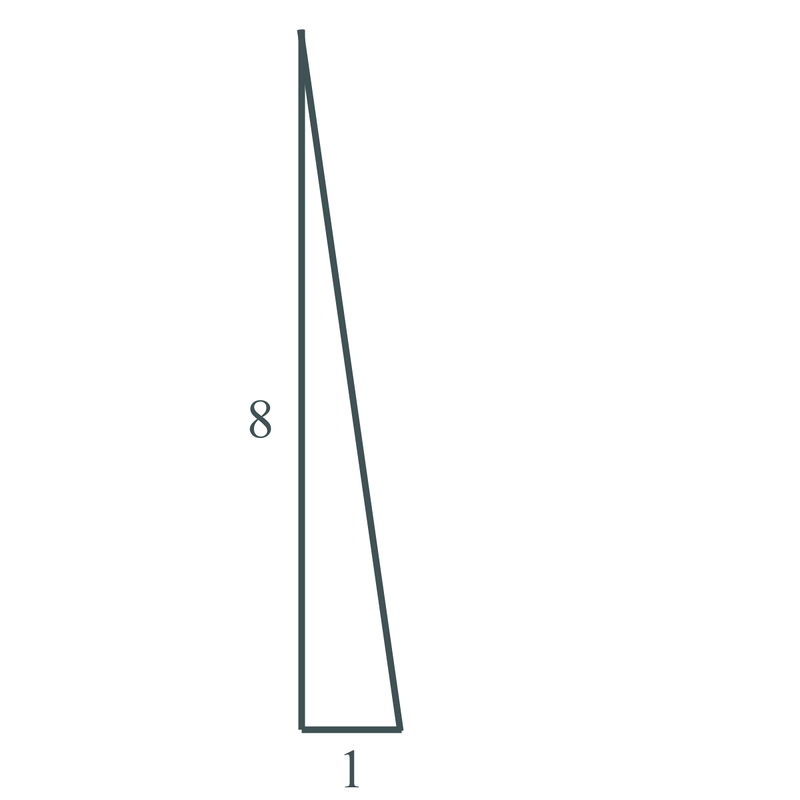
Solución

\(a=1\),\(b=8\), necesitamos encontrar la hipotenusa.

\(\begin{align*} 1^2+8^2 &= c^2 \\ 1+64 &= c^2 \\ 65 &= c^2 \\ \sqrt{65} &= c\end{align*}\)

Ejemplo\(\PageIndex{3}\)

Usa el Teorema de Pitágoras para encontrar el lado faltante del siguiente triángulo:

Figura\(\PageIndex{6}\)

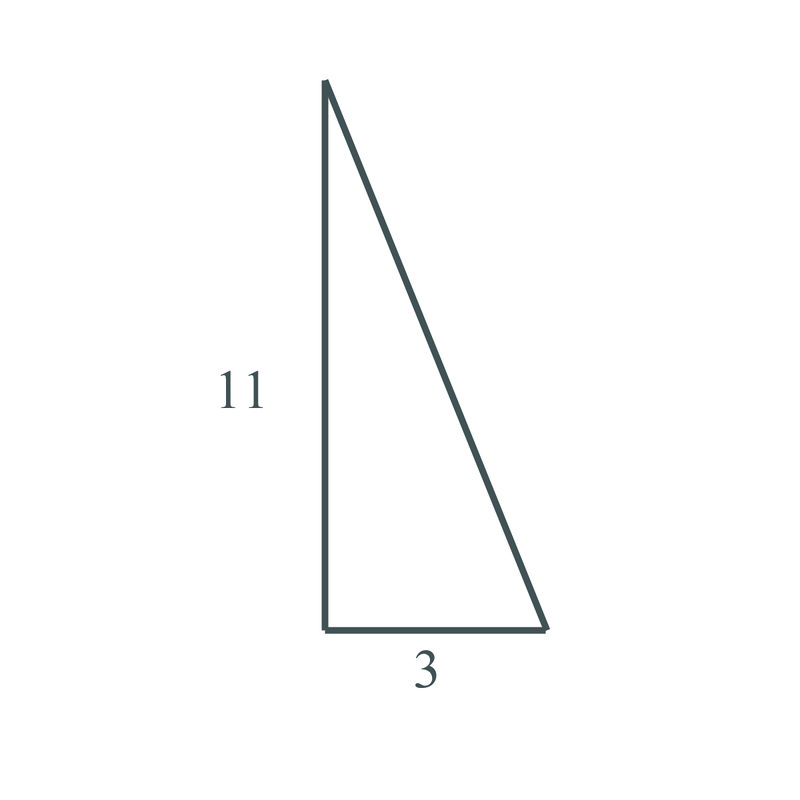
Solución

\(a=3\),\(b=11\), necesitamos encontrar la longitud del lado\(c\), la hipotenusa.

\(\begin{align*} 3^2+11^2 &= c^2 \\ 9+121 &= c^2 \\ 130 &= c^2 \\ \sqrt{130} &= c \end{align*}\)

Ejemplo\(\PageIndex{4}\)

Encuentra el lado que falta del triángulo rectángulo a continuación. Deja la respuesta en forma radical más simple.

Figura\(\PageIndex{7}\)

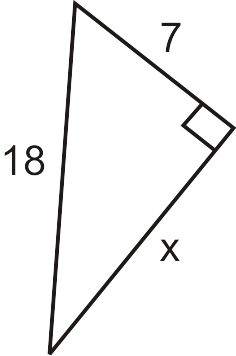
Solución

a=7, c=18, necesitamos encontrar la longitud del lado\(b\).

\(\begin{align*} 7^2+b^2 &= 18^2 \\ 49+b^2 &= 18^2 \\ 324−49 &= b^2 \\ 275 &= b^2 \\ \sqrt{275} &= b\end{align*} \)

Revisar

Encuentra los lados faltantes de los triángulos rectos. Deja las respuestas en forma radical más simple.

1. Si las patas de un triángulo rectángulo son 3 y 4, entonces la hipotenusa es _____________.
2. Si las patas de un triángulo rectángulo son 6 y 8, entonces la hipotenusa es _____________.
3. Si las patas de un triángulo rectángulo son 5 y 12, entonces la hipotenusa es _____________.
4. Si los lados de un cuadrado son de longitud 6, entonces la diagonal es _____________.
5. Si los lados de un cuadrado son 9, entonces la diagonal es _____________.
6. Si los lados de un cuadrado son\(x\), entonces la diagonal es _____________.
7. Si las patas de un triángulo rectángulo son 3 y 7, entonces la hipotenusa es _____________.
8. Si las patas de un triángulo rectángulo son\(2\sqrt{5}\) y 6, entonces la hipotenusa es _____________.
9. Si una pata de un triángulo rectángulo es 4 y la hipotenusa es 8, entonces la otra pierna es _____________.
10. Si una pata de un triángulo rectángulo es 10 y la hipotenusa es 15, entonces la otra pierna es _____________.
11. Si una pata de un triángulo rectángulo es\(4\sqrt{7}\) y la hipotenusa es\(10\sqrt{6}\), entonces la otra pierna es _____________.
12. Si las patas de un triángulo rectángulo son\(x\) y\(y\), entonces la hipotenusa es ____________.

Prueba del teorema de Pitágoras

Usa la imagen de abajo para responder a las siguientes preguntas.

Figura\(\PageIndex{8}\)

13. Encuentra el área de la plaza en la imagen con lados (a+b).
14. Encuentra la suma de las áreas del cuadrado con lados c y los triángulos rectos con patas a y b.
15. Explique por qué las áreas encontradas en los dos problemas anteriores deben tener el mismo valor. Después, establecer las expresiones iguales entre sí y simplificar para obtener el Teorema de Pitágoras.

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 1.1.

El vocabulario

Término	Definición
Teorema de Pitágoras	El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectángulo\(a^2+b^2=c^2\), dada por, donde a y b son patas del triángulo y c es la hipotenusa del triángulo.

Recursos adicionales

Elemento Interactivo

Práctica: Aplicaciones del teorema de Pitágoras