4.33: Teorema de Pitágoras y su Converse
- Page ID
- 107485
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Usa a-cuadrado + b-cuadrado = c-cuadrado para demostrar que los triángulos son triángulos rectos.
Supongamos que está montando una tienda de campaña, y un poste de 8 pies hace un ángulo recto con el suelo. Si una cuerda va desde la parte superior del poste a un punto en el suelo a 12 pies de distancia de la base del poste, ¿cuánto dura la cuerda? ¿Cómo calcularías su longitud?
Teorema de Pitágoras y su Converse
El teorema de Pitágoras
Uno de los teoremas más importantes en matemáticas y ciencias es el Teorema de Pitágoras. En pocas palabras, afirma: “La suma del cuadrado de cada pata de un triángulo rectángulo es igual al cuadrado de la hipotenusa”.
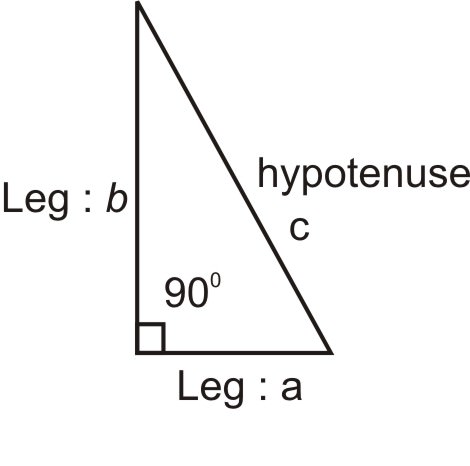
Un triángulo rectángulo es un triángulo con un ángulo recto. Repasemos la anatomía básica del triángulo rectángulo.
Los dos segmentos que forman el ángulo recto (\(90^{\circ}\)) se denominan patas del triángulo recto. El segmento opuesto al ángulo recto se llama hipotenusa.
El Teorema de Pitágoras afirma\((leg_1)^2+(leg_2)^2=(hypotenuse)^2\):
\(a^2+b^2=c^2\)
O, para encontrar la hipotenusa,\(c=\sqrt{a^2+b^2}\).
Observe que esta relación sólo es cierta para los triángulos rectos. En cursos posteriores, aprenderás a determinar las relaciones con triángulos no rectos.
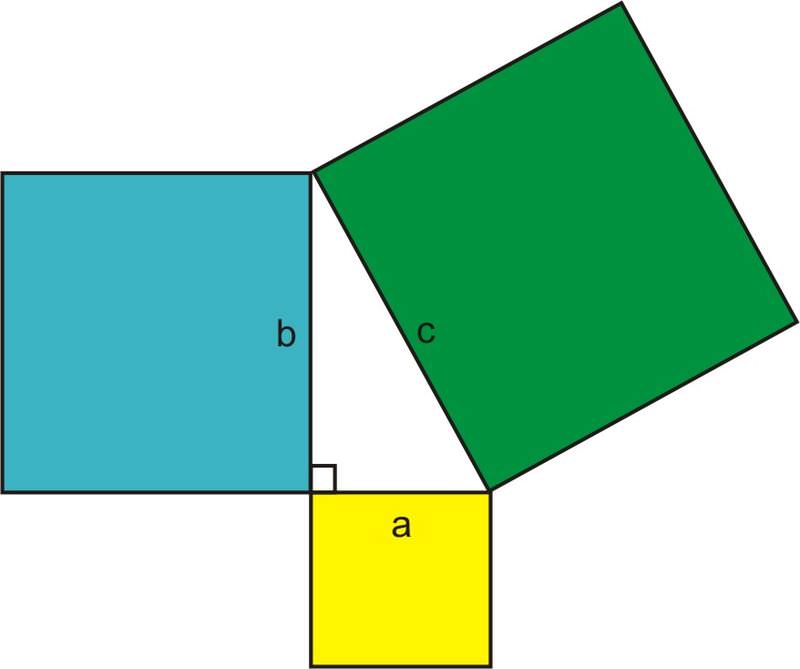
Aunque usualmente nos referimos al Teorema de Pitágoras al determinar las longitudes laterales de un triángulo rectángulo, el teorema originalmente hizo una declaración sobre las áreas. Si construimos cuadrados a cada lado de un triángulo rectángulo, el Teorema de Pitágoras dice que el área del cuadrado cuyo lado es la hipotenusa es igual a la suma de las áreas de los cuadrados formados por las patas del triángulo.
El Converso del Teorema de Pitágoras
También es cierto lo Converse del Teorema de Pitágoras. Es decir, si las longitudes de tres lados de un triángulo hacen que la ecuación sea\(a^2+b^2=c^2\) verdadera, entonces representan los lados de un triángulo rectángulo.
Con este converse, puedes usar el Teorema de Pitágoras para demostrar que un triángulo es un triángulo rectángulo, aunque no conozcas ninguna de las medidas de ángulo del triángulo.
Completemos los siguientes problemas relacionados con los triángulos rectos y el Teorema de Pitágoras:
- ¿El triángulo de abajo contiene un ángulo recto?
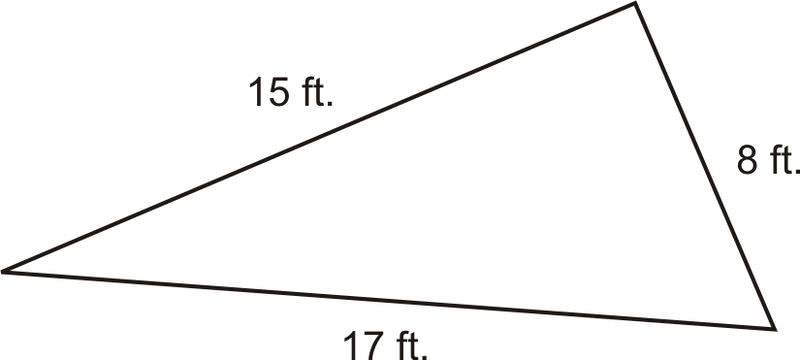
Este triángulo no tiene marcas de ángulo recto ni ángulos medidos, por lo que no puedes asumir que sabes si el triángulo es agudo, recto u obtuso con solo mirarlo. Tómese un momento para analizar las longitudes de los lados y ver cómo están relacionados. Dos de los lados, 15 y 17, son relativamente cercanos en longitud. El tercer lado, 8, es aproximadamente la mitad de la longitud de los dos lados más largos.
Para ver si el triángulo podría ser correcto, intente sustituir las longitudes de los lados en el Teorema de Pitágoras para ver si hacen que la ecuación sea verdadera. La hipotenusa es siempre el lado más largo, por lo que 17 debe ser sustituido por c. Los otros dos valores pueden representar a y b y el orden no es importante.
\(\begin{align*} a^2+b^2&=c^2 \\ 8^2+15^2&=17^2 \\ 64+225&=289 \\ 289&=289\end{align*}\)
Dado que ambos lados de la ecuación son iguales, estos valores satisfacen el Teorema de Pitágoras. Por lo tanto, el triángulo descrito en el problema es un triángulo rectángulo.
- Una pata de un triángulo rectángulo es 5 más que la otra pierna. La hipotenusa es una más del doble del tamaño de la pierna corta. Encuentra las dimensiones del triángulo.
Dejar x= longitud de la pierna corta. Entonces,\(x+5= length\:of \:the \:long \:leg\) y\(2x+1= length \:of \:the \:hypotenuse\).
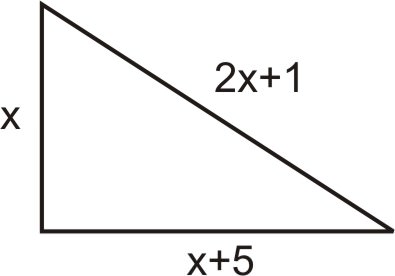
Los lados del triángulo deben satisfacer el Teorema de Pitágoras.
\(\begin{align*} & & x^2+(x+5)^2 &=(2x+1) \\ &Eliminate \:the \:parentheses. &\qquad x^2+x^2+10x+25 &=4x^2+4x+1 \\ &Move \:all \:terms \:to \:the \:right \:hand \:side \:of \:the \:equation. &\qquad 0 &=2x^2−6x−24 \\ &Divide \:all \:terms \:by \:2. &\qquad 0 &=x^2−3x−12 \\ &Solve \:using \:the \:quadratic \:formula. &\qquad x &=\dfrac{3 \pm \sqrt{9+48}}{2}=\dfrac{3 \pm \sqrt{57}}{2} \\ & & x &\neq 5.27 \:or \:x\neq −2.27 \end{align*}\)
La solución negativa no tiene sentido en el contexto de este problema. Entonces, usa\(x=5.27\) y obtenemos
\(short\:−leg=5.27,\: long\:−leg=10.27\)y
\(hypotenuse=11.54\).
- Encuentra el área de la región sombreada en el siguiente diagrama.
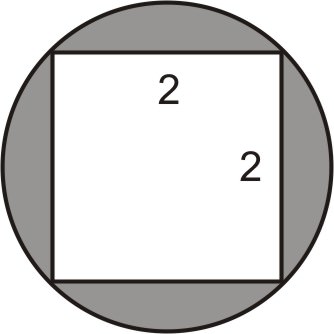
Dibuja la diagonal del cuadrado sobre la figura.
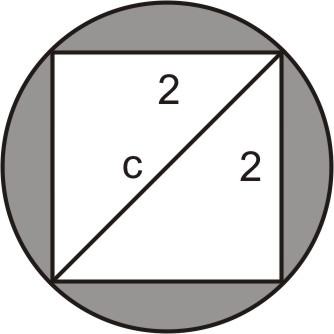
Observe que la diagonal del cuadrado es también el diámetro del círculo.
Definir variables. Vamos\(c= diameter\: of\: the\: circle\).
\(\begin{align*} & & 2^2+2^2 &= c^2 \\ & & 4+4 &=c^2 \\ &Write\: the \:formula \:and \:solve. \: & c^2 & = 8\Rightarrow c=\sqrt{8}\Rightarrow c=2\sqrt{2}\end{align*}\)
El diámetro del círculo es\(2\sqrt{2}\). Por lo tanto, el radio es\(r=\sqrt{2}\).
El área de un círculo es\(A=\pi r^2=\pi (\sqrt{2} )^2=2\pi\).
El área de la región sombreada es, por lo tanto, 2\ pi −4\ neq 2.28\).
Ejemplo\(\PageIndex{1}\)
Anteriormente, te pidieron que encontraras el largo de una cuerda que usabas para armar una tienda de campaña. Sabes que la cuerda va desde la parte superior de un poste de 8 pies hasta un punto en el suelo a 12 pies de distancia de la base.
Solución
Esta situación puede ser representada por un triángulo rectángulo.
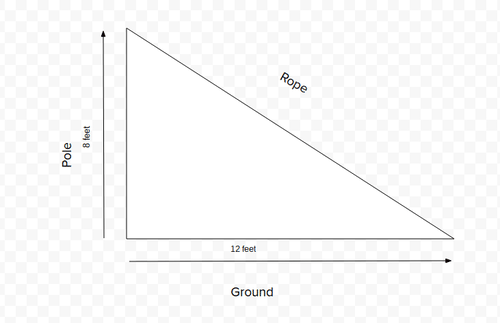
Suponiendo que el ángulo entre el suelo y el poste es de 90 grados, podemos usar el Teorema de Pitágoras para resolver por la longitud de la cuerda.
Dejar\(a= 8 \:feet (length of the pole), \(b= 12\:feet\) (la distancia desde el poste a la cuerda en el suelo), y\(c= the\:length \:of \:the \:rope\).
\(\begin{align*}a^2+b^2&=c^2 \\ 8^2+12^2&=c^2 \\ 208&=c^2 \\ c&=\sqrt{208} \\ c&=\sqrt{16}\sqrt{13} \\ c&=4\sqrt{13}\:feet \end{align*}\)
La cuerda mide\(4\sqrt{13} \) pies de largo.
Ejemplo\(\PageIndex{2}\)
Determinar si un triángulo con lados de longitudes 5, 6 y 8 forma o no un triángulo rectángulo.
Solución
Usa el Converse del Teorema de Pitágoras:
\(\begin{align*} Start \:with \:the \:Pythagorean \:equation.&\qquad a^2+b^2 &=c^2 \\ Substitute \:in \:the \:values \:of \:the\: sides. &\qquad 5^2+6^2&\stackrel{?}{=}8^2 \\ Simplify. &\qquad 25+36 &\stackrel{?}{=}64 \\ Check. &\qquad 61 &\neq 64\end{align*} \)
Dado que estas longitudes de lados no satisfacen la ecuación del Teorema de Pitágoras, el triángulo no es un triángulo rectángulo.
Revisar
Verifica que cada triángulo sea un triángulo rectángulo.
- \(a=12, \:b=9,\:c=15\)
- \(a=6, \:b=6, \:c=6\sqrt{2}\)
- \(a=8, \:b=8\sqrt{3}, \:c=16\)
Encuentra la longitud que falta de cada triángulo rectángulo.
- \(a=12,\: b=16, \:c=?\)
- \(a=?, \:b=20, \:c=30\)
- \(a=4, \:b=?, \:c=11\)
-
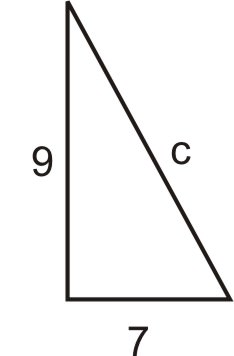
Figura\(\PageIndex{8}\) -
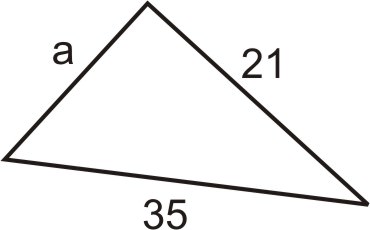
Figura\(\PageIndex{9}\) -
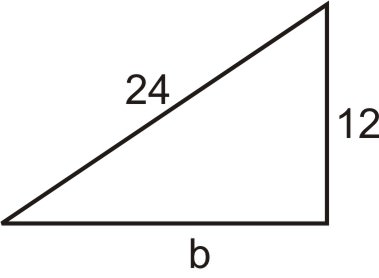
Figura\(\PageIndex{10}\) - Una pata de un triángulo rectángulo es 4 pies menos que la hipotenusa. La otra pierna mide 12 pies. Encuentra las longitudes de los tres lados del triángulo.
- Una pata de un triángulo rectángulo es 3 más del doble de la longitud de la otra. La hipotenusa es 3 veces la longitud de la pierna corta. Encuentra los largos de las tres patas del triángulo.
- Un diamante de béisbol de regulación es un cuadrado con 90 pies entre bases. ¿A qué distancia está la segunda base del plato casero?
- Emanuel tiene una caja de cartón que mide\(20\: cm\times 10\: cm\times 8\: cm\) (\(length\times width\times height\)). ¿Cuál es la longitud de la diagonal desde una esquina inferior hasta la esquina superior opuesta?
- Samuel coloca una escalera contra su casa. La base de la escalera está a 6 pies de la casa y la escalera mide 10 pies de largo. ¿Qué tan alto sobre el suelo toca la escalera la pared de la casa?
- Encuentra el área del triángulo usando la fórmula\(A=\dfrac{1}{2}base\times height\).
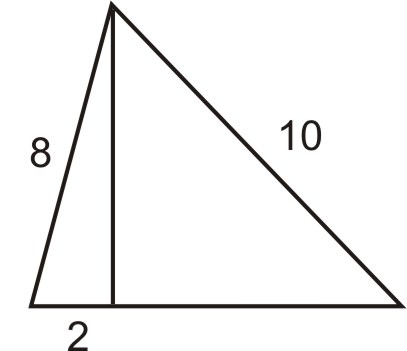
Figura\(\PageIndex{11}\) - En lugar de caminar por los dos lados de un campo rectangular, Mario decidió cortar a través de la diagonal. Guarda una distancia que es la mitad del lado largo del campo. Encuentra la longitud del lado largo del campo dado que el lado corto es de 123 pies.
- Marcus navega hacia el norte y Sandra navega hacia el este desde el mismo punto de partida. En dos horas, el barco de Marcus está a 35 millas del punto de partida y el barco de Sandra está a 28 millas del punto de partida. ¿A qué distancia están los barcos el uno del otro?
- Determinar el área del círculo.
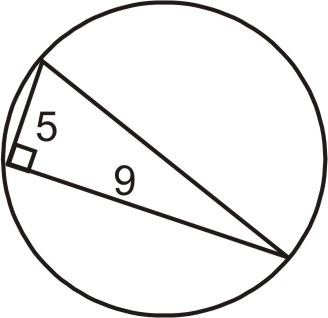
Figura\(\PageIndex{12}\) - En un triángulo rectángulo, una pata es el doble de larga que la otra y el perímetro es 28. ¿Cuáles son las medidas de los lados del triángulo?
- María tiene una hoja rectangular para galletas que mide\(10\:inches\times 14\:inches\). Encuentra la longitud de la diagonal de la hoja para galletas.
- Mike está cargando una camioneta en movimiento caminando por una rampa. La rampa mide 10 pies de largo y la cama de la camioneta está a 2.5 pies sobre el suelo. ¿Hasta dónde se extiende la rampa más allá de la parte trasera de la camioneta?
Quiz Rápido
- Identificar el origen de\(h(x)=\sqrt{x−2}+5\), y luego graficar la función.
- Simplificar\(6\sqrt[3]{2}\) racionalizando el denominador.
- Simplificar:\(\sqrt[4]{−32}\). Si la respuesta no es posible, explique por qué.
- ¿Qué es una solución extraña? ¿En qué situaciones ocurren tales soluciones?
- ¿Pueden los lados con longitudes de 3, 4 y 6 formar un triángulo rectángulo?
- Resolver\(5=y+\sqrt[3]{y+6}\).
vocabulario
| Término | Definición |
|---|---|
| converse del Teorema de Pitágoras | Si las longitudes de los tres lados de un triángulo satisfacen la ecuación\(a^2+b^2=c^2\), entonces el triángulo es un triángulo rectángulo. |
| converse | Si una declaración condicional es\(p\rightarrow q\) (si\(p\), entonces\(q\)), entonces lo contrario es\(q\rightarrow p\) (si\(q\), entonces\(p\). Tenga en cuenta que lo contrario de una declaración no es cierto solo porque la declaración original es verdadera. |
| Hipotenusa | La hipotenusa de un triángulo rectángulo es el lado más largo del triángulo rectángulo. Está frente al ángulo recto. |
| Piernas de un triángulo rectángulo | Las patas de un triángulo rectángulo son los dos lados más cortos del triángulo rectángulo. Las patas están adyacentes al ángulo recto. |
| Teorema de Pitágoras | El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectángulo\(a^2+b^2=c^2\), dada por, donde a y b son patas del triángulo y c es la hipotenusa del triángulo. |
Recursos adicionales
Elemento Interactivo
Video: Teorema de Pitágoras - Resumen
Actividades: Teorema de Pitágoras y sus preguntas de discusión Converse
Práctica: El teorema de Pitágoras y su Converse
Mundo real: Mapa SF - Pyththm

