5.3: Área y Perímetro Cuadrados y Rectangulares
- Page ID
- 107554
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Calcular las medidas de borde y cobertura de cuadriláteros rectilíneos, dadas las medidas lineales.
Área y Perímetro de Rectángulos
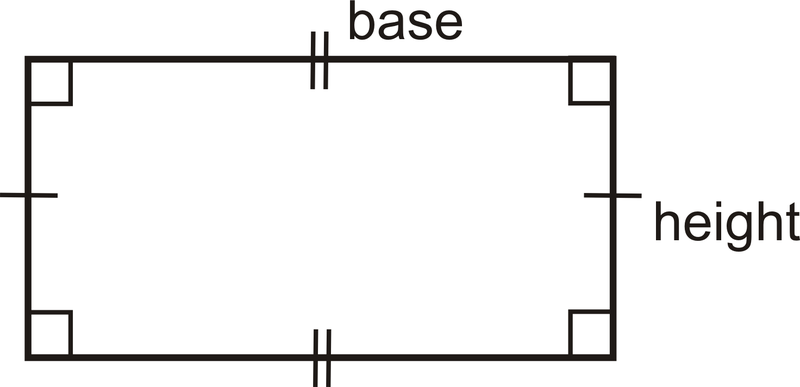
Para encontrar el área de un rectángulo, calcule\(A=bh\), donde\(b\) está la base (ancho) y\(h\) es la altura (largo). El perímetro de un rectángulo siempre lo será\(P=2b+2h\).
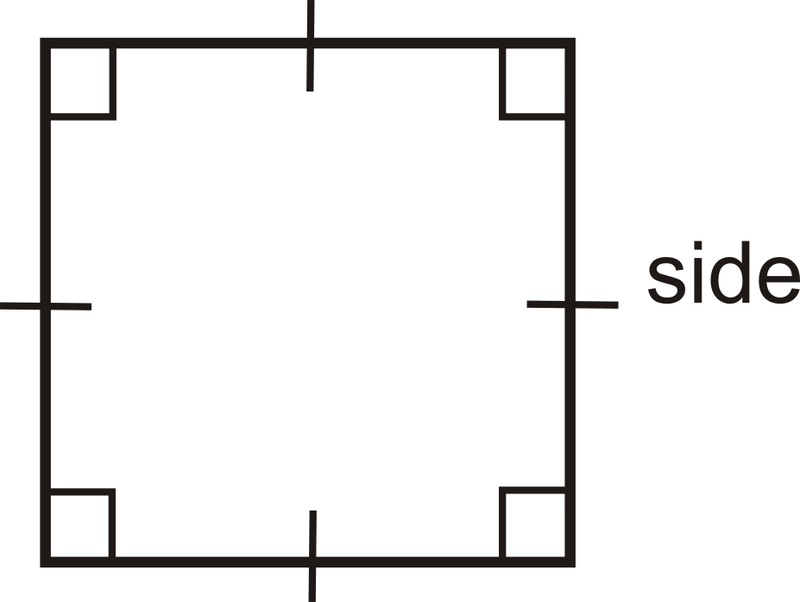
Si un rectángulo es un cuadrado, con lados de longitud s, entonces perímetro es\(P_{square}=2s+2s=4s\) y área es\(A_{sqaure}=s\cdot s=s^2\).
¿Y si te dieran un rectángulo y el tamaño de su base y altura? ¿Cómo podrías encontrar la distancia total alrededor del rectángulo y la cantidad de espacio que ocupa?
Ejemplo\(\PageIndex{1}\)
El área de un cuadrado es\(75\text{ in}^2\). Encuentra el perímetro.
Solución
Para encontrar el perímetro, necesitamos encontrar la longitud de los costados.
\(\begin{aligned} A&=s^2=75\text{ in}^2 \\ s&=\sqrt{75}=5\sqrt{3}\text{ in } \end{aligned}\)
A partir de esto,\(P=4(5\sqrt{3})=20\sqrt{3}\text{ in }\)
Ejemplo\(\PageIndex{2}\)
Dibuja dos rectángulos diferentes con un área de\(36\text{ cm^2 }\).
Solución
Piense en todos los diferentes factores de 36. Todas estas pueden ser dimensiones de los diferentes rectángulos.
Otras posibilidades podrían ser\(6\times 6\),\(2\times 18\), y\(1\times 36\).
Ejemplo\(\PageIndex{3}\)
Encuentra el área y perímetro de un rectángulo con lados\(4\text{ cm }\) por\(9\text{ cm }\).
Solución
El perímetro es\(4+9+4+9=26\text{ cm }\). El área es\(A=9\cdot 4=36\text{ cm}^2\).
Ejemplo\(\PageIndex{4}\)
Encuentra el área y perímetro de una plaza con costado\(5\text{ in }\).
Solución
El perímetro es\(4(5)=20\:in\) y el área es\(5^2=25\text{ in}^2\).
Ejemplo\(\PageIndex{5}\)
Encuentra el área y perímetro de un rectángulo con lados\(13\text{ m }\) y\(12\text{ m}^2\).
Solución
El perímetro es\(2(13)+2(12)=50\text{ m }\). El área es\(13(12)=156\text{ m}^2\).
Revisar
- Encuentra el área y perímetro de un cuadrado con lados de longitud\(12\text{ in }\).
- Encuentra el área y perímetro de un rectángulo con altura de\(9\text{ cm }\) y base de\(16\text{ cm }\).
- Encuentra el área y perímetro de un rectángulo si la altura es 8 y la base es 14.
- Encuentra el área y perímetro de una plaza si los lados están\(18\text{ ft }\).
- Si el área de una plaza es\(81\text{ ft}^2\), encuentra el perímetro.
- Si el perímetro de una plaza es\(24\text{ in }\), encuentra el área.
- El perímetro de un rectángulo es 32. Encuentra dos dimensiones diferentes que podría ser el rectángulo.
- Dibuja dos rectángulos diferentes que alberguen un área de\(90\text{ mm}^2\).
- Verdadero o falso: Para un rectángulo, cuanto mayor sea el perímetro, mayor será el área.
- Encuentra el perímetro y área de un rectángulo con lados\(17\text{ in }\) y\(21\text{ in }\).
El vocabulario
| Término | Definición |
|---|---|
| zona | La cantidad de espacio dentro de una figura. El área se mide en unidades cuadradas. |
| perimetral | La distancia alrededor de una forma. El perímetro de cualquier figura debe tener una unidad de medida adherida al mismo. Si no se dan unidades específicas (pies, pulgadas, centímetros, etc), escriba unidades. |
| Área de un Rectángulo | Para encontrar el área '\(A\)' de un rectángulo, calcule\(A = bh\), donde\(b\) está la base (ancho) y h es la altura (largo). |
| Perímetro de un Rectángulo | El perímetro '\(P\)' de un rectángulo es igual al doble de la base agregada al doble de la altura:\(P = 2b + 2h\). |
Recursos adicionales
Elemento Interactivo
Video: Determinar el área de un rectángulo que involucra números enteros
Actividades: Área y Perímetro de Rectángulos Preguntas de Discusión
Ayudas de estudio: Guía de estudio de triángulos y cuadriláteros
Práctica: Área y Perímetro Cuadrados y Rectangulares
Mundo Real: Perímetro