1.19: Área de Polígonos y Círculos
- Page ID
- 110957
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Puede usar una calculadora para la mayor parte de este módulo según sea necesario.
Hemos visto que el perímetro de un polígono es la distancia alrededor del exterior. El perímetro es una longitud, que es unidimensional, y así se mide en unidades lineales (pies, centímetros, millas, etc.). El área de un polígono es la cantidad de espacio bidimensional dentro del polígono, y se mide en unidades cuadradas: pies cuadrados, centímetros cuadrados, millas cuadradas, etc.
Siempre se puede pensar en el área como el número de cuadrados requeridos para rellenar completamente la forma.
1. Encuentra el área de este rectángulo.
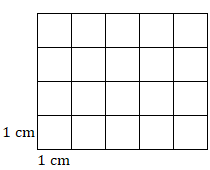
2. Encuentra el área de esta plaza.
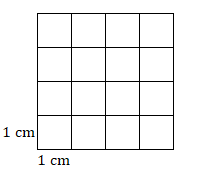
- Contestar
-
1. \(20\text{ cm}^2\)
2. \(16\text{ cm}^2\)
Rectángulos y Cuadrados
Por supuesto, hay fórmulas para encontrar las áreas de rectángulos y cuadrados; no tenemos que contar cuadraditos.
Área de un Rectángulo
\(A=lw\)[1] o\(A=bh\)
Área de un cuadrado
\[A=s^2 \nonumber \]
Encuentra el área de cada figura.
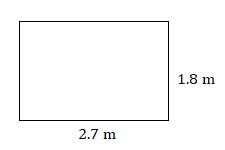
3. 
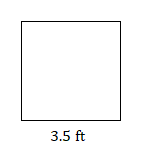
4. 
- Contestar
-
3. \(4.86\text{ m}^2\)
4. \(12.25\text{ ft}^2\)
Paralelogramos
Otro polígono común es el paralelogramo, que parece un rectángulo inclinado. Como su nombre lo indica, los pares de lados opuestos son paralelos y tienen la misma longitud. Observe que, si etiquetamos un lado como base del paralelogramo, tenemos una altura perpendicular que no es la longitud de los otros lados.
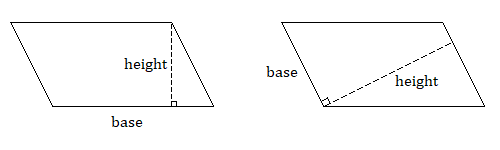
El siguiente conjunto de diagramas muestra que podemos cortar parte de un paralelogramo y reorganizar las piezas en un rectángulo con la misma base y altura que el paralelogramo original. Un paralelogramo con una base de\(7\) unidades y una altura vertical de\(6\) unidades se transforma en un\(7\) por\(6\) rectángulo, con un área de unidades\(42\) cuadradas.
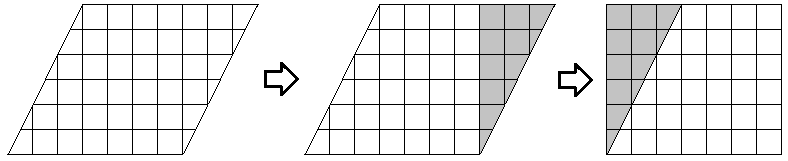
Por lo tanto, la fórmula para el área de un paralelogramo es idéntica a la fórmula para el área de un rectángulo, siempre que tengamos cuidado de usar la base y la altura, que debe ser perpendicular.
Área de un paralelogramo
\(A=bh\)
Encuentra el área de cada paralelogramo.
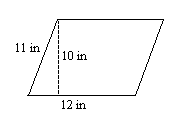
5. 
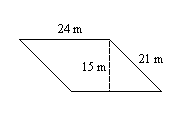
6. 
- Contestar
-
5. \(120\text{ in}^2\)
6. \(360\text{ m}^2\)
Triángulos
Cuando necesitamos encontrar el área de un triángulo, necesitamos identificar una base y una altura que sea perpendicular a esa base. Si el triángulo es obtuso, tal vez tengas que imaginar la altura fuera del triángulo y extender la línea base para encontrarla.
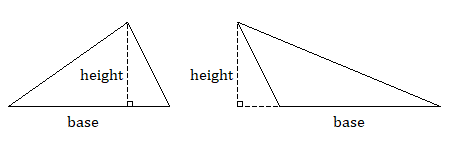
Como se muestra a continuación, cualquier triángulo se puede duplicar para formar un paralelogramo. Por lo tanto, el área de un triángulo es la mitad del área de un paralelogramo con la misma base y altura.
Área de un Triángulo
\(A=\dfrac{1}{2}bh\)o\(A=bh\div2\)
Al igual que con un paralelogramo, recuerda que la altura debe ser perpendicular a la base.
Encuentra el área de cada triángulo.
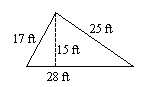
7. 
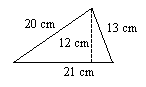
8. 
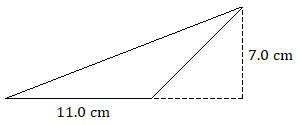
9. 
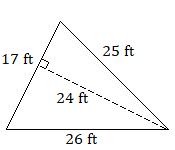
10. 
- Contestar
-
7. \(210\text{ ft}^2\)
8. \(126\text{ cm}^2\)
9. \(38.5\text{ cm}^2\)
10. \(204\text{ ft}^2\)
Trapecios
Un cuadrilátero algo menos común es el trapecio, que tiene exactamente un par de lados paralelos, a los que llamamos las bases. El primer ejemplo que se muestra a continuación se llama trapecio isósceles porque, al igual que un triángulo isósceles, sus dos lados no paralelos tienen longitudes iguales.
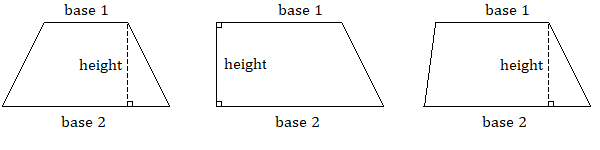
Hay varias formas de mostrar de dónde viene la fórmula del área, pero las explicaciones son mejores en video porque pueden ser animadas. [2] [3] [4]
Área de un trapecio
\[A=\dfrac{1}{2}h(b_1+b_2) \nonumber \]
o
\[A=(b_1+b_2)h\div2 \nonumber \]
No se deje intimidar por los subíndices en\(b_1\) y\(b_2\); es solo una manera de nombrar dos medidas diferentes usando la misma letra para la variable. (Mucha gente llama a las bases\(a\) y\(b\) en su lugar; siéntase libre de escribirlo de la manera que prefiera). Como sea que los llames, solo tienes que sumar las dos bases, multiplicar por la altura, y tomar la mitad de eso.
Encuentra el área de cada trapecio.
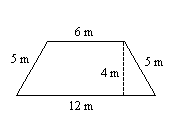
11. 
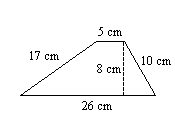
12. 
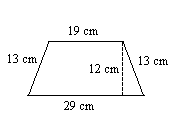
13. 
- Contestar
-
11. \(36\text{ m}^2\)
12. \(124\text{ cm}^2\)
13. \(288\text{ cm}^2\)
Círculos
El área de un círculo es\(\pi\) multiplicada por el cuadrado del radio:\(A=\pi{r^2}\). Las unidades siguen siendo unidades cuadradas, a pesar de que un círculo es redondo. (Piense en los cuadrados en un waffle redondo.) Debido a que no podemos colocar un número entero de cuadrados —o una fracción exacta de cuadrados— dentro del círculo, el área de un círculo será una aproximación.
Área de un círculo
\ [A=\ pi {r^2}\)]
Recuerden eso\(\pi\approx3.1416\).
Encuentra el área de cada círculo. Redondear a la décima más cercana o a tres cifras significativas, lo que parezca apropiado.
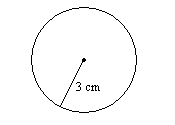
14. 
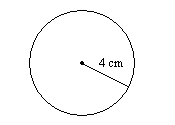
15. 
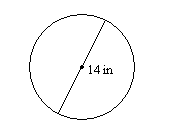
16. 
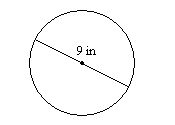
17. 
Cada figura es una fracción de un círculo. Calcular cada área.
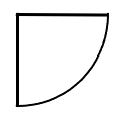
18. El radio del cuarto de círculo es\(5\) metros.
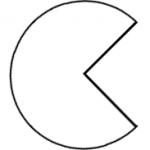
19. Se ha quitado un cuarto de círculo de un círculo con un diámetro de\(7\) pies.
- Contestar
-
14. \(28.3\text{ cm}^2\)
15. \(50.3\text{ cm}^2\)
16. \(153.9\text{ in}^2\)
17. \(63.6\text{ in}^2\)
18. \(19.6\text{ m}^2\)
19. \(28.9\text{ ft}^2\)
- Puede optar por usar letras mayúsculas para las variables aquí porque una letra minúscula “l” puede confundirse fácilmente con un número “1".
- [1]https://youtu.be/yTnYRpcZA9c
- [2]https://youtu.be/WZtO3oERges
- [3]https://youtu.be/uLHc6Br2veg