4.3: Optimización

Última actualización
Guardar como PDF

Page ID: 111757

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la Sección 3.1 aprendimos sobre los valores extremos, los valores más grandes y menores que una función alcanza en un intervalo. Motivamos nuestro interés en tales valores discutiendo cómo tenía sentido querer conocer los valores más altos/más bajos de una acción, o el más rápido/más lento que un objeto se estaba moviendo. En esta sección aplicamos los conceptos de valores extremos para resolver “problemas verbales”, es decir, problemas planteados en términos de situaciones que requieren que creamos el marco matemático adecuado en el que resolver el problema.

Comenzamos con un ejemplo clásico al que le sigue una discusión sobre el tema de la optimización.

Ejemplo$\PageIndex{1}$: Optimization: perimeter and area

Un hombre tiene 100 pies de esgrima, un patio grande y un perro pequeño. Quiere crear un recinto rectangular para su perro con el cercado que le proporcione el área máxima. ¿Qué dimensiones proporcionan el área máxima?

Solución

Es probable que uno pueda adivinar la respuesta correcta —eso es genial. Procederemos a mostrar cómo el cálculo puede proporcionar esta respuesta en un contexto que demuestre que esta respuesta es correcta.

Ayuda a hacer un boceto de la situación. Nuestro recinto está bosquejado dos veces en Figura$\PageIndex{1}$, ya sea con pasto verde y bonitas tablas de cerco o como un simple rectángulo. De cualquier manera, dibujar un rectángulo nos obliga a darnos cuenta de que necesitamos conocer las dimensiones de este rectángulo para poder crear una función de área —después de todo, estamos tratando de maximizar el área.

$alt$

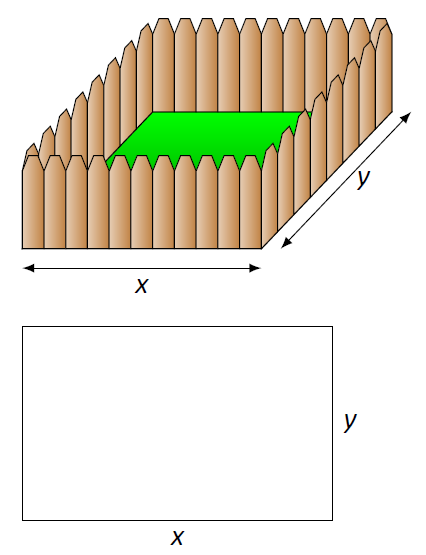
Figura$\PageIndex{1}$: Un boceto del recinto en Ejemplo$\PageIndex{1}$.

Dejamos$x$ y$y$ denotamos las longitudes de los lados del rectángulo. Claramente,

\[\text{Area}=xy.\]

Todavía no sabemos manejar funciones con 2 variables; necesitamos reducirlo a una sola variable. Sabemos más de la situación: el hombre tiene 100 pies de esgrima. Al conocer que el perímetro del rectángulo debe ser 100, podemos crear otra ecuación:

\[\text{Perimeter} = 100 = 2x+2y.\]

Ahora tenemos 2 ecuaciones y 2 incógnitas. En esta última ecuación, resolvemos para$y$:

\[y = 50-x.\]

Ahora sustituya esta expresión por$y$ en la ecuación de área:

\[ \text{Area} = A(x) = x(50-x).\]

Tenga en cuenta que ahora tenemos una ecuación de una variable; realmente podemos llamar al Área una función de$x$.

Esta función sólo tiene sentido cuando$0\leq x \leq 50$, de lo contrario obtenemos valores negativos de área. Entonces encontramos los valores extremos de$A(x)$ en el intervalo$[0,50]$.

Para encontrar los puntos críticos, tomamos la derivada de$A(x)$ y la establecemos igual a 0, luego resolvemos para$x$.

\[\begin{align} A(x) &= x(50-x) \\ &= 50x-x^2 \\ A'(x) &= 50-2x \end{align}\]

Resolvemos$50-2x=0$ encontrar$x=25$; este es el único punto crítico. Evaluamos$A(x)$ en los puntos finales de nuestro intervalo y en este punto crítico para encontrar los valores extremos; en este caso, lo único que nos importa es el máximo.

Claramente$A(0)=0$ y$A(50)=0$, mientras que$A(25) = 625 \text{ft}^2$. Este es el máximo. Como antes encontramos$y = 50-x$, encontramos que también$y$ es$25$. Así las dimensiones del recinto rectangular con perímetro de 100 pies con área máxima es un cuadrado, con lados de longitud 25 pies.

Este ejemplo es muy simplista y un poco ideado. (Después de todo, la mayoría de las personas crean un diseño y luego compran cercas para satisfacer sus necesidades, y no compran cercas y planean más tarde). Pero modela bien el proceso necesario: crear ecuaciones que describan una situación, reducen una ecuación a una sola variable, luego encuentran el valor extremo necesario.

“En la vida real”, los problemas son mucho más complejos. Las ecuaciones a menudo no son reducibles a una sola variable (por lo tanto, se necesita cálculo multivariable) y las ecuaciones en sí mismas pueden ser difíciles de formar. Comprender los principios aquí proporcionará una buena base para las matemáticas que probablemente encontrará más adelante.

Aquí se esboza el proceso básico para resolver estos problemas de optimización.

Idea Clave 6: Solución de Problemas de Optimización

Entender el problema. Identifique claramente qué cantidad se va a maximizar o minimizar. Haz un boceto si es útil.
Crear ecuaciones relevantes al contexto del problema, utilizando la información proporcionada. (Una de ellas debe describir la cantidad a optimizar. A esto lo llamaremos la ecuación fundamental.)
Si la ecuación fundamental define la cantidad a optimizar en función de más de una variable, reducirla a una sola función variable usando sustituciones derivadas de las otras ecuaciones.
Identificar el dominio de esta función, teniendo en cuenta el contexto del problema.
Encuentra los valores extremos de esta función en el dominio determinado.
Identificar los valores de todas las cantidades relevantes del problema.

Utilizaremos Key Idea 6 en una variedad de ejemplos.

Ejemplo$\PageIndex{2}$: {Optimization: perimeter and area

Aquí hay otro problema clásico del cálculo: Una mujer tiene un cercado de 100 pies, un perro pequeño y un patio grande que contiene un arroyo (que en su mayoría es recto). Ella quiere crear un recinto rectangular con área máxima que utilice el arroyo como un lado. (Al parecer su perro no se va a nadar.) ¿Qué dimensiones proporcionan el área máxima?

Solución

Seguiremos los pasos descritos por Key Idea 6.

Estamos maximizando el área. Un boceto de la región ayudará; La figura$\PageIndex{2}$ da dos bocetos del área cerrada propuesta. Una característica clave de los bocetos es reconocer que un lado no está cercado.

$alt$

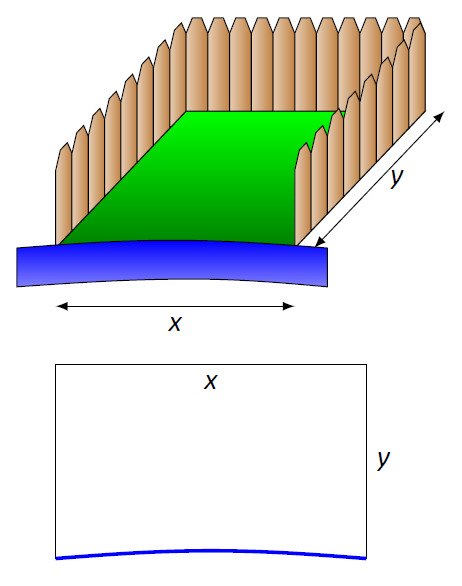
Figura$\PageIndex{2}$: Un boceto del recinto en Ejemplo$\PageIndex{2}$.

Queremos maximizar el área; como en el ejemplo anterior, $$\ text {Área} = xy.$$ Esta es nuestra ecuación fundamental. Esto define el área como una función de dos variables, por lo que necesitamos otra ecuación para reducirla a una variable.
Nuevamente apelamos al perímetro; aquí el perímetro es $$\ text {Perímetro} = 100 = x+2y.$$ Observe cómo esto es diferente que en nuestro ejemplo anterior.
Ahora reducimos la ecuación fundamental a una sola variable. En la ecuación perimetral, resolver para$y$:$y = 50 - x/2$. Ahora podemos escribir Área como $$\ texto {Área} = A (x) = x (50-x/2) = 50x -\ frac12x^2.$$ El área ahora se define como una función de una variable.
Queremos que el área no sea negativa. Ya que$A(x) = x(50-x/2)$, queremos$x\geq 0$ y$50-x/2\geq 0$. Esta última desigualdad implica eso$x\leq100$, así$0\leq x\leq 100$.
Ahora encontramos los valores extremos. En los puntos finales, se encuentra el mínimo, dando un área de 0.
Encuentra los puntos críticos. Tenemos$A'(x) = 50-x$; estableciendo esto igual a 0 y resolviendo para$x$ retornos$x=50$. Esto da un área de $$A (50) = 50 (25) = 1250. $$
Nosotros antes establecimos$y = 50-x/2$; así$y = 25$. Así nuestro rectángulo tendrá dos lados de longitud 25 y un lado de largo 50, con un área total de 1250 pies$^2$.

Tenga en cuenta al hacer estos problemas que estamos practicando un proceso; es decir, estamos aprendiendo a convertir una situación en un sistema de ecuaciones. Estas ecuaciones nos permiten escribir una cierta cantidad en función de una variable, que luego optimizamos.

Ejemplo$\PageIndex{3}$: Optimization: minimizing cost

Una línea eléctrica debe funcionar desde una central eléctrica ubicada en la playa hasta una instalación en alta mar. La figura$\PageIndex{3}$ muestra las distancias entre la central eléctrica y la instalación.

Cuesta $50/ft. hacer funcionar una línea eléctrica a lo largo del terreno, y $130/ft. hacer funcionar una línea eléctrica bajo el agua. ¿Cuánto de la línea eléctrica se debe correr a lo largo del terreno para minimizar el costo general? ¿Cuál es el costo mínimo?

$alt$

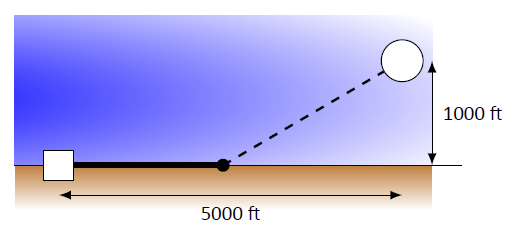
Figura$\PageIndex{3}$: Funcionamiento de una línea eléctrica desde la central eléctrica hasta una instalación en alta mar con un costo mínimo en Ejemplo$\PageIndex{3}$

Solución

Seguiremos la estrategia de Key Idea 6 implícitamente, sin numerar específicamente los pasos.

Hay dos soluciones inmediatas que podríamos considerar, cada una de las cuales rechazaremos a través del “sentido común”. Primero, podríamos minimizar la distancia conectando directamente las dos ubicaciones con una línea recta. Sin embargo, esto requiere que todo el cable se coloque bajo el agua, la opción más costosa. En segundo lugar, podríamos minimizar la longitud bajo el agua pasando un cable de 5000 pies a lo largo de la playa, directamente frente a la instalación en alta mar. Esto tiene el efecto no deseado de tener la distancia más larga de todas, probablemente asegurando un costo no mínimo.

La solución óptima probablemente tiene que correr la línea a lo largo del suelo por un tiempo, luego bajo el agua, como implica la figura. Necesitamos etiquetar nuestras distancias desconocidas: la distancia recorrida a lo largo del suelo y la distancia corre bajo el agua. Reconociendo que la distancia submarina se puede medir como la hipotenusa de un triángulo rectángulo, elegimos etiquetar las distancias como se muestra en la Figura$\PageIndex{4}$.

$alt$

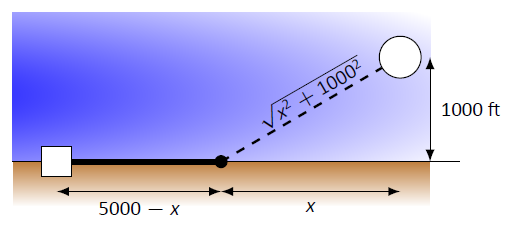
Figura$\PageIndex{4}$: Etiquetar distancias desconocidas en el Ejemplo$\PageIndex{3}$.

Al elegir$x$ como lo hicimos, hacemos sencilla la expresión bajo la raíz cuadrada. Ahora creamos la función de costo.

$$
\ begin {array} {ccccc}
\ text {Costo} &=&\ text {costo del terreno} &+ &\ text {costo del agua}\\
& &\ text {\ $50}\ veces\ texto {distancia terrestre} &+&\ texto {\ $130}\ veces\ texto {distancia del agua}\\
& & 50 (5000-x) &+& 130\ sqrt {x^2+ 1000^2}. \\
\ fin {matriz}
\]

Así que tenemos$c(x) = 50(5000-x)+ 130\sqrt{x^2+1000^2}$. Esta función sólo tiene sentido en el intervalo$[0,5000]$. Si bien estamos bastante seguros de que los puntos finales no darán un costo mínimo, seguimos evaluando$c(x)$ en cada uno para verificar.

$$c (0) = 380,000\ quad\ quad c (5000)\ aprox 662,873.\]

Ahora encontramos los valores críticos de$c(x)$. Calculamos$c'(x)$ como

$$c' (x) = -50+\ frac {130x} {\ sqrt {x^2+1000^2}}.\]

Reconocer que esto nunca es indefinido. Configurando$c'(x)=0$ y resolviendo$x$, contamos con:

\[ \begin{align} -50+\frac{130x}{\sqrt{x^2+1000^2}} &= 0 \\ \frac{130x}{\sqrt{x^2+1000^2}} &= 50\\ \frac{130^2x^2}{x^2+1000^2} &= 50^2\\ 130^2x^2 &= 50^2(x^2+1000^2) \\ 130^2x^2-50^2x^2 &= 50^2\cdot1000^2\\ (130^2-50^2)x^2 &= 50,000^2\\ x^2 &= \frac{50,000^2}{130^2-50^2}\\ x &= \frac{50,000}{\sqrt{130^2-50^2}}\\ x & = \frac{50,000}{120} =416\frac23\approx 416.67. \end{align}\]

Evaluar$c(x)$ a$x=416.67$ da un costo de alrededor de $370,000. La distancia a la que se coloca la línea eléctrica a lo largo de la tierra es de$5000-416.67 = 4583.33$ pies y la distancia submarina es de$\sqrt{416.67^2+1000^2} \approx 1083$ pies.

En los ejercicios verás una variedad de situaciones que requieren combinar habilidades de resolución de problemas con cálculo. Enfócate en el proceso; aprende a formar ecuaciones a partir de situaciones que pueden ser manipuladas en lo que necesitas. Evite memorizar cómo hacer “este tipo de problema” en lugar de “ese tipo de problema”. Aprender un proceso beneficiará a uno mucho más tiempo que memorizar una técnica específica.

La siguiente sección introduce nuestra aplicación final de la derivada: diferenciales. Dado$y=f(x)$, ofrecen un método para aproximar el cambio en$y$ después de$x$ los cambios en una pequeña cantidad.