1.8: Perímetro y Circunferencia

Última actualización
Guardar como PDF

Page ID: 110958

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Puede usar una calculadora a lo largo de este módulo si es necesario.

Perímetro

Un polígono es una figura geométrica cerrada con lados rectos. Polígonos comunes incluyen triángulos, cuadrados, rectángulos, paralelogramos, trapezoides, pentágonos, hexágonos, octágonos... El perímetro de un polígono es la distancia alrededor del exterior. En general, para encontrar el perímetro de un polígono, se pueden sumar las longitudes de todos sus lados.

Además, si aún no lo has hecho, ahora es el momento de adquirir el hábito de incluir unidades en tus respuestas.

Ejercicios$\PageIndex{1}$

1. Encuentra el perímetro del triángulo.

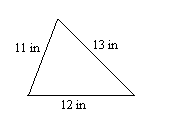
$triángulo con lados etiquetados 11 in, 13 in, 12 in$

2. Encuentra el perímetro del trapecio.

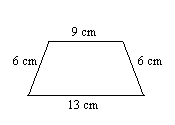
$trapecio con lados etiquetados 6 cm, 9 cm, 6 cm, 13 cm$

Responder

1. $36$en

2. $34$cm

Si sabemos que algunos de los lados de un polígono son iguales, podemos usar una fórmula como alternativa para sumar todas las longitudes individualmente. La primera fórmula que se muestra a continuación utiliza la variable$s$ para el lado de un cuadrado. Las fórmulas de rectángulo utilizan$l$ para la longitud y$w$ para el ancho, o$b$ para la base y$h$ para la altura; estos términos son intercambiables.

Formulas perimetrales

Cuadrado:$P=4s$

Rectángulo:$P=2l+2w$ o$P=2b+2h$

Rectángulo:$P=2(l+w)$ o$P=2(b+h)$

Ejercicios$\PageIndex{1}$

3. Encuentra el perímetro de la plaza.

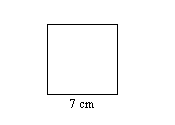
$cuadrado con lado inferior etiquetado 7 cm$

4. Encuentra el perímetro del rectángulo.

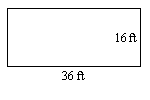
$rectángulo con lado derecho etiquetado 16 pies y lado inferior etiquetado 36 pies$

5. Un área de almacenamiento, que es un rectángulo que mide$45$ pies de largo y$20$ pies de ancho, necesita ser cercado alrededor de los cuatro lados. ¿Cuántos pies de esgrima se requieren? (Para que sea simple, ignore cualquier puerta u otras complicaciones.)

6. Giancarlo está poniendo molduras de corona alrededor del borde del techo de su sala de estar. Si la habitación es un rectángulo$12$ de pie por$16$ pie, ¿cuánta moldura de corona necesita?

Responder

3. $28$cm

4. $104$ft

5. $130$ft

6. $56$ft

Los lados de un polígono regular son todos iguales en longitud. Por lo tanto, multiplicar la longitud de un lado por el número de lados nos dará el perímetro.

Fórmula perimetral

Polígono regular con$n$ lados de longitud$s$:

\[P=n\cdot{s} \nonumber \]

Ejercicios$\PageIndex{1}$

Encuentra el perímetro de cada polígono regular.

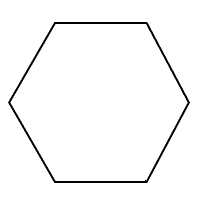
7. Cada lado del hexágono tiene$4$ pulgadas de largo.

$un hexágono regular (6 lados)$

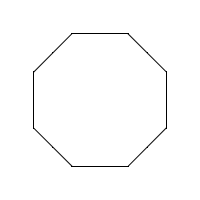
8. Cada lado del octágono tiene$2.5$ centímetros de largo.

$un octágono regular (8 lados)$

Responder

7. $24$en

8. $20$cm

Circunferencia

En lugar de llamarlo perímetro, la distancia alrededor del exterior del círculo se llama circunferencia. Repasemos un poco de vocabulario circular antes de seguir adelante.

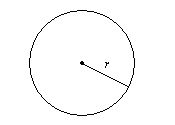
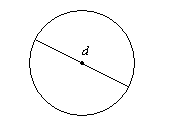
Cada punto de un círculo está a la misma distancia de su centro. Esta distancia desde el centro hasta el borde del círculo se llama radio. La distancia de un borde a otro, a través del centro del círculo, se llama diámetro. Como puede ver, el diámetro es el doble de la longitud del radio.

$un círculo con una línea desde el centro hasta el borde, etiquetada con r$ $un círculo con una línea de borde a borde pasando por el centro, etiquetada como d$

A lo largo de la historia, diferentes civilizaciones han descubierto que la circunferencia de un círculo es ligeramente más que$3$ veces la longitud de su diámetro. Para el año 2000 a. C., los babilonios estaban usando el valor$3\dfrac{1}{8}=3.125$ y los egipcios estaban usando el valor$3\dfrac{13}{81}\approx3.1605$. ^[1] El valor$3\dfrac{1}{7}\approx3.1429$ es una aproximación aún mejor para la relación entre la circunferencia y el diámetro. Sin embargo, el valor real no puede escribirse como una fracción exacta. Es el número irracional$\pi$, pronunciado “pastel”, que es aproximadamente$3.14159$.

Fórmulas de circunferencia

\[C=\pi{d} \nonumber \]

\[C=2\pi{r} \nonumber \]

Cualquier calculadora científica tendrá una$\pi$ clave; usar esto le dará el resultado más preciso, aunque debe estar seguro de redondear su respuesta adecuadamente. (Consulte este módulo si necesita un repaso sobre redondeo con multiplicación o división). Mucha gente usa$3.14$ como aproximación para$\pi$, pero esto puede llevar a un error de redondeo; si debes usar una aproximación,$3.1416$ es mejor que$3.14$.

A veces doblamos las reglas en este libro de texto y le pedimos redondear a un cierto valor positorio en lugar de redondear a un cierto número de dígitos significativos.

Ejercicios$\PageIndex{1}$

Calcular la circunferencia de cada círculo. Redondear a la décima más cercana.

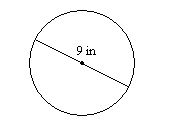
9. $un círculo con diámetro etiquetado 9 pulg$

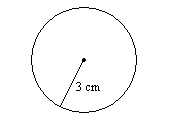
10. $un círculo con radio etiquetado 3 cm$

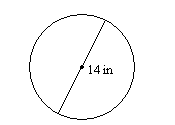
11. $un círculo con diámetro etiquetado 14 pulg$

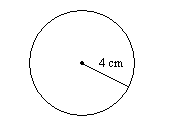
12. $un círculo con radio etiquetado 4 cm$

Responder

9. $28.3$en

10. $18.8$cm

11. $44.0$en

12. $25.1$cm

Esta información proviene del Capítulo 1 del libro A History of Pi de Petr Beckmann. Se trata de una lectura sorprendentemente interesante.

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)