5.7: Clasificación cuadrilátero
- Page ID
- 107483
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Categoriza los cuadriláteros en función de lados y ángulos. Identificarlos visualmente, y por descripción. Encuentra longitudes y ángulos, determina formas y prueba congruencia y si las líneas son paralelas.

Rasha está ayudando a su padre a pintar el marco de la puerta de su casa. Ella llama a gritar los nombres de cada forma que pinta. Ella alcanza una forma que no puede nombrar. Ella ve que tiene cuatro lados y un conjunto de lados paralelos. ¿Qué forma está pintando?
En este concepto, aprenderás a identificar y clasificar los cuadriláteros.
Clasificación de cuadriláteros
Los polígonos son formas cerradas con lados formados por líneas. Cualquier forma cerrada con bordes rectos, como un triángulo o rectángulo, es un polígono.
Los polígonos con cuatro lados, como rectángulos y cuadrados, se denominan cuadriláteros . El prefijo de esta palabra “quad” significa cuatro, por lo tanto, un cuadrilátero es un polígono que tiene cuatro lados. Los cuadriláteros también tienen cuatro ángulos, y estos cuatro ángulos tienen una suma de 360°. Esto es cierto para todos los cuadriláteros
Otra característica importante de los cuadriláteros es que muchos tienen uno o incluso dos pares de lados paralelos. Mira los cuadriláteros a continuación.
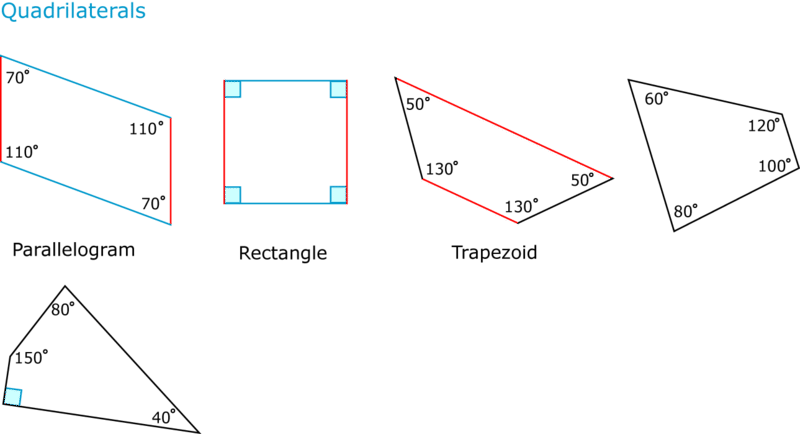
Veamos en detalle los diferentes tipos de cuadriláteros.
Un paralelogramo es un cuadrilátero con lados opuestos paralelos. La primera figura anterior es un paralelogramo. Hay algunas características especiales de los paralelogramos. Una es que cada par de lados paralelos es congruente. En la primera figura anterior, los dos lados cortos tienen la misma longitud y los dos lados largos son de la misma longitud. Esta relación especial entre los pares de lados afecta los ángulos de un paralelogramo: los ángulos opuestos entre sí son congruentes. Los ángulos de 70° son opuestos entre sí, y los ángulos de 110° son opuestos entre sí. Esta relación existe en cualquier paralelogramo, sin importar la longitud de los lados o los tamaños de los pares angulares.
Hay tres tipos especiales de paralelogramos.
Un rectángulo es un cuadrilátero porque tiene cuatro lados, y es un paralelogramo porque tiene dos pares de lados paralelos congruentes. Los cuatro ángulos son ángulos rectos.
Un cuadrado tiene dos pares de lados paralelos y cuatro ángulos rectos. Sus cuatro lados son congruentes.
El tercer paralelogramo especial se llama rombo . Al igual que un cuadrado, un rombo tiene cuatro lados congruentes y pares de ángulos congruentes opuestos entre sí. Sin embargo, no se requieren ángulos rectos para un rombo. Entonces un rombo puede ser un cuadrado, pero un cuadrado no es necesariamente un rombo debido a los ángulos rectos necesarios en un cuadrado.
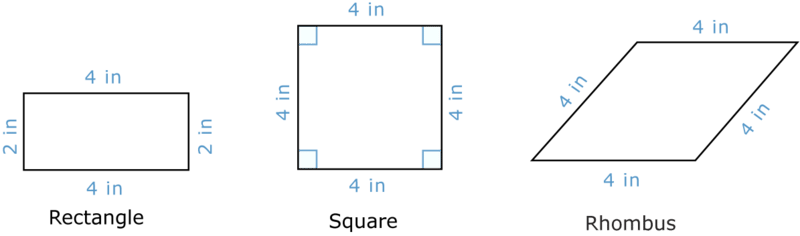
Veamos un ejemplo.
Identifique la forma de abajo como un rectángulo, cuadrado, rombo o simplemente un paralelogramo.
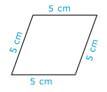
Primero, revisa los largos de los lados.
La forma tiene cuatro lados de igual longitud.
A continuación, comprueba si la forma tiene cuatro ángulos rectos.
La forma no tiene cuatro ángulos rectos.
Después, identifica la forma.
Rombo.
La respuesta es un rombo.
Ahora veamos otro cuadrilátero especial.
Un trapecio es un cuadrilátero que tiene solo un par de lados paralelos.
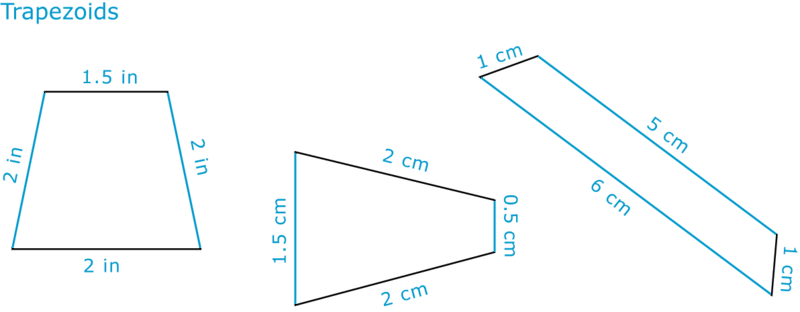
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Rasha y el marco de la puerta de su casa.
Pinta una forma que tiene cuatro lados y un juego de lados paralelos. ¿Qué forma está pintando?
Solución
Primero, verifique el número de lados.
La forma tiene cuatro lados.
A continuación, comprueba si la forma tiene lados paralelos.
La forma tiene un conjunto de lados paralelos.
Después, identifica la forma.
Trapezoide.
La respuesta es que Rasha está pintando un trapecio.
Ejemplo\(\PageIndex{2}\)
Identifique la forma de abajo como un rectángulo, cuadrado, rombo o paralelogramo.
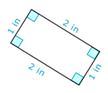
Solución
Primero, revisa los largos de los lados.
Los lados opuestos son congruentes.
A continuación, comprueba si la forma tiene cuatro ángulos rectos.
La forma tiene cuatro ángulos rectos.
Después, identifica la forma.
Rectángulo.
La respuesta es rectángulo.
Ejemplo\(\PageIndex{3}\)
Identificar cada tipo de cuadrilátero con base en su descripción.
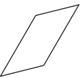
Solución
Primero, revisa los largos de los lados.
Se desconoce la longitud de los lados, pero los lados opuestos parecen ser congruentes.
A continuación, comprueba si la forma tiene cuatro ángulos rectos.
La forma no tiene cuatro ángulos rectos.
Después, identifica la forma.
Paralelogramo.
La respuesta es paralelogramo.
Ejemplo\(\PageIndex{4}\)
Una figura de cuatro lados con lados opuestos paralelos y congruentes con cuatro ángulos rectos.
Solución
Primero, verifique el número de lados.
La forma tiene cuatro lados.
A continuación, anote la relación entre los lados opuestos.
Los lados opuestos son paralelos y congruentes.
Después, clasifique la forma.
Cuadrado.
La respuesta es un cuadrado.
Ejemplo\(\PageIndex{5}\)
Una figura de cuatro lados con dos pares de lados paralelos. Los lados opuestos son congruentes.
Solución
Primero, verifique el número de lados.
La forma tiene cuatro lados.
A continuación, anote la relación entre los lados opuestos.
Los lados opuestos son paralelos y los lados paralelos son congruentes.
Después, clasifique la forma.
Paralelogramo.
La respuesta es un paralelogramo.
Revisar
Identifique cada cuadrilátero como un paralelogramo, rectángulo, cuadrado, rombo o trapecio.
-

Figura\(\PageIndex{8}\) -

Figura\(\PageIndex{9}\) -

Figura\(\PageIndex{10}\) -

Figura\(\PageIndex{11}\)
Mira cada imagen y nombra el cuadrilátero que se muestra en la foto.
-

Figura\(\PageIndex{12}\) -

Figura\(\PageIndex{13}\) -

Figura\(\PageIndex{14}\) -

Figura\(\PageIndex{15}\) -

Figura\(\PageIndex{16}\)
Nombra la figura geométrica que se describe a continuación o responde a cada pregunta.
- Tiene cuatro lados y cuatro ángulos
- Tiene un par de lados opuestos que son paralelos
- Tiene cuatro ángulos rectos y cuatro lados congruentes
- Un paralelogramo con cuatro ángulos rectos.
- Un paralelogramo con cuatro lados congruentes
- Tiene cuatro ángulos rectos y lados opuestos congruentes
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Kite | Una cometa es un cuadrilátero con distintos lados congruentes adyacentes. |
| Paralelogramo | Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. |
| Polígono | Un polígono es una simple figura cerrada con al menos tres lados rectos. |
| Cuadrilátero | Un cuadrilátero es una figura cerrada con cuatro lados y cuatro vértices. |
| Rectángulo | Un rectángulo es un cuadrilátero con cuatro ángulos rectos. |
| Rombo | Un rombo es un cuadrilátero con cuatro lados congruentes. |
| Trapezoide | Un trapecio es un cuadrilátero con exactamente un par de lados opuestos paralelos. |
Recursos adicionales
Elemento Interactivo
Video: Propiedades cuadriláteros
Actividades: Clasificación cuadrilátero Preguntas de discusión
Ayudas de estudio: Guía de estudio de paralelogramos
Práctica: Clasificación cuadrilátero
Mundo Real: Clasificación Cuadrilátero

