5.8: Clasificación de paralelogramo
- Page ID
- 107548
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los rectángulos, rombos y cuadrados son paralelogramos definidos por sus diagonales, ángulos y lados.
Clasificación de paralelogramos
Rectángulos, rombos (también llamados rombos) y cuadrados son todas versiones más específicas de paralelogramos, también llamados paralelogramos especiales.
- Un cuadrilátero es un rectángulo si y solo si tiene cuatro ángulos rectos (congruentes).
\(ABCD\)es un rectángulo si y solo si\(\angle A\cong \angle B\cong \angle C\cong \angle D\).
- Un cuadrilátero es un rombo si y sólo si tiene cuatro lados congruentes.
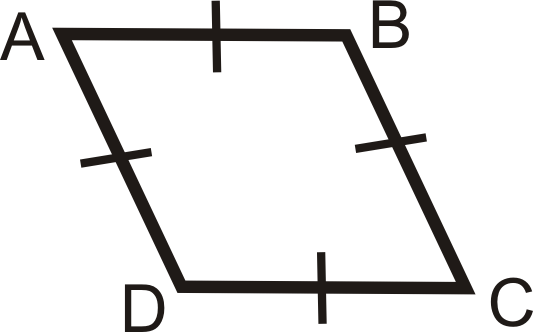
\(ABCD\)es un rombo si y solo si\(\overline{AB}\cong \overline{BC} \cong \overline{CD} \cong \overline{AD}\).
- Un cuadrilátero es un cuadrado si y sólo si tiene cuatro ángulos rectos y cuatro lados congruentes. Por definición, un cuadrado es un rectángulo y un rombo.
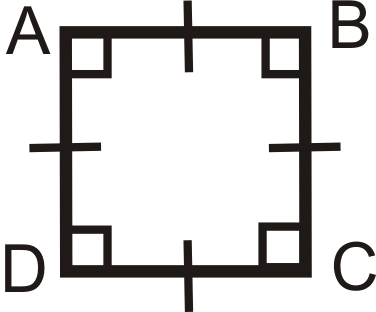
\(ABCD\)es un cuadrado si y sólo si\(\angle A\cong \angle B\cong \angle C\cong \angle D\) y\(\overline{AB}\cong \overline{BC} \cong \overline{CD} \cong \overline{AD}\).
Siempre se puede mostrar que un paralelogramo es un rectángulo, rombo o cuadrado usando las definiciones de estas formas. Hay algunas formas adicionales de probar que los paralelogramos son rectángulos y rombos, que se muestran a continuación:
1. Un paralelogramo es un rectángulo si las diagonales son congruentes.
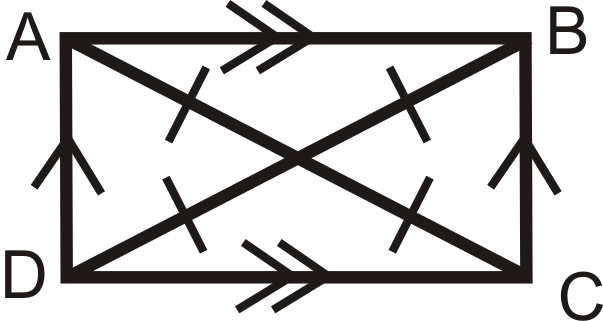
\(ABCD\)es paralelogramo. Si\(\overline{AC}\cong \overline{BD}\), entonces también\(ABCD\) es un rectángulo.
2. Un paralelogramo es un rombo si las diagonales son perpendiculares.
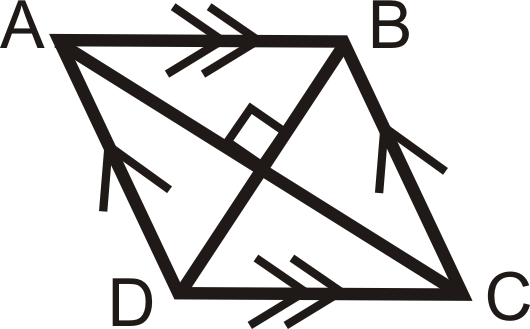
\(ABCD\)es un paralelogramo. Si\(\overline{AC}\perp \overline{BD}\), entonces también\(ABCD\) es un rombo.
3. Un paralelogramo es un rombo si las diagonales bisecan cada ángulo.
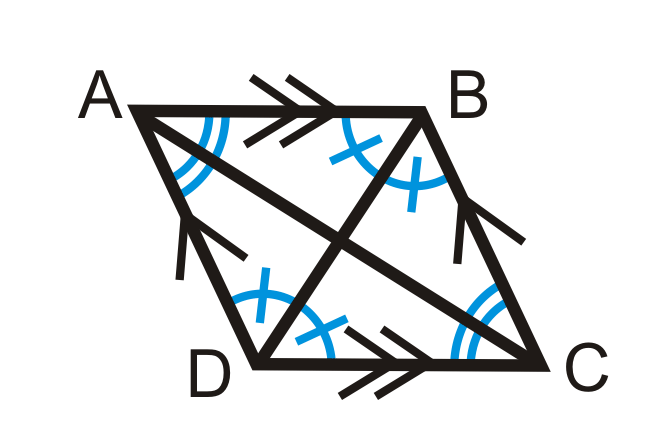
\(ABCD\)es un paralelogramo. Si\(\overline{AC}\) bisectas\(\angle BAD\) y\(\angle BCD\) y\(\overline{BD}\) bisectas\(\angle ABC\) y\(\angle ADC\), entonces también\(ABCD\) es un rombo.
¿Y si te dieran un paralelogramo e información sobre sus diagonales? ¿Cómo podrías usar esa información para clasificar el paralelogramo como rectángulo, rombo y/o cuadrado?
Ejemplo\(\PageIndex{1}\)
¿Es un rectángulo A VECES, SIEMPRE, o NUNCA un paralelo Explique por qué.
Solución
Un rectángulo tiene dos juegos de lados paralelos, por lo que SIEMPRE es un paralelogramo.
Ejemplo\(\PageIndex{2}\)
¿Es un cuadrilátero A VECES, SIEMPRE, o NUNCA un pent Explique por qué.
Solución
Un cuadrilátero tiene cuatro lados, por lo que NUNCA será un pentágono con cinco lados.
Ejemplo\(\PageIndex{3}\)
¿Qué tipo de paralelogramo son las cifras a continuación?
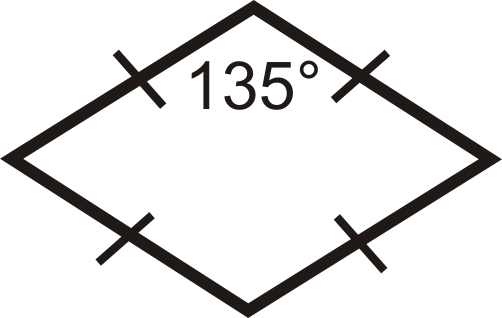
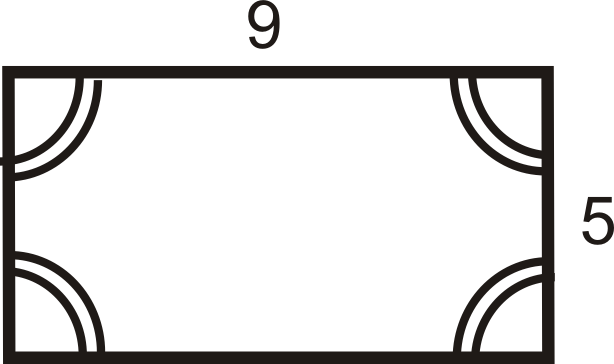
Solución
Para la primera figura, todos los lados son congruentes y un ángulo lo es\(135^{\circ}\), por lo que los ángulos no son congruentes. Esto es un rombo.
Para la segunda figura, los cuatro ángulos son congruentes pero los lados no lo son. Esto es un rectángulo.
Ejemplo\(\PageIndex{4}\)
¿Un rombo A VECES, SIEMPRE, O NUNCA es cuadrado? Explique por qué.
Solución
Un rombo tiene cuatro lados congruentes y un cuadrado tiene cuatro lados y ángulos congruentes. Por lo tanto, un rombo es un cuadrado cuando tiene ángulos congruentes. Esto significa que un rombo es a VECES un cuadrado.
Ejemplo\(\PageIndex{5}\)
Enumere todo lo que sabe de la plaza\(SQRE\).
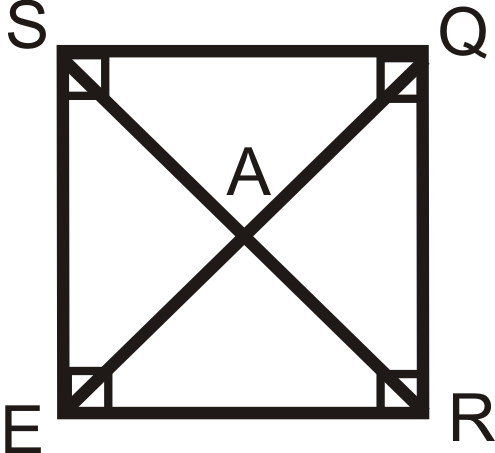
Solución
Un cuadrado tiene todas las propiedades de un paralelogramo, rectángulo y rombo.
| Propiedades de un Paralelogramo | Propiedades de un Rombo | Propiedades de un Rectángulo |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
Todos los ángulos bisectados son\(45^{\circ}\).
Revisar
- \(RACE\)es un rectángulo. Encuentra:
- \(RG\)
- \(AE\)
- \(AC\)
- \(EC\)
- \(m\angle RAC\)
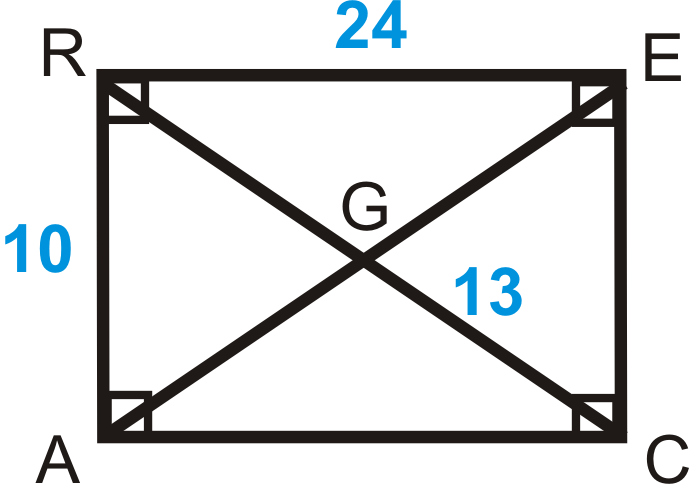Figura\(\PageIndex{10}\) - \(DIAM\)es un rombo. Encuentra:
- \(MA\)
- \(MI\)
- \(DA\)
- \(m\angle DIA\)
- \(m\angle MOA\)
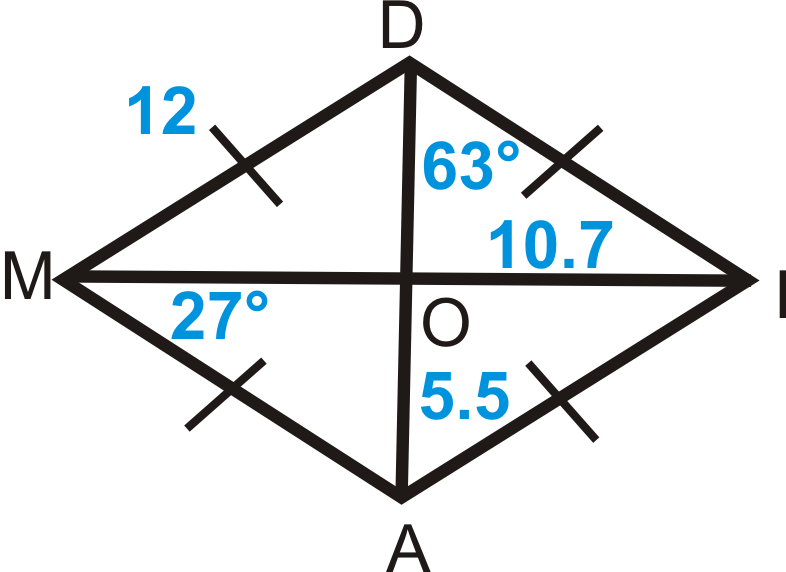Figura\(\PageIndex{11}\) - \(CUBE\)es un cuadrado. Encuentra:
- \(m\angle UCE\)
- \(m\angle EYB\)
- \(m\angle UBY\)
- \(m\angle UEB\)
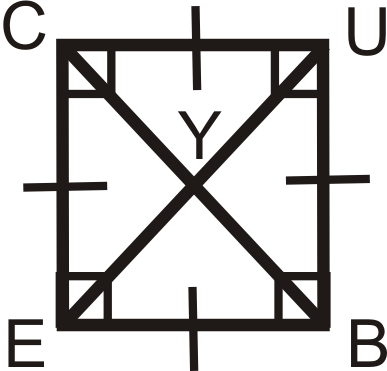
Figura\(\PageIndex{12}\)
Para las preguntas 4-15, determinar si el cuadrilátero es un paralelogramo, rectángulo, rombo, cuadrado o ninguno.
-
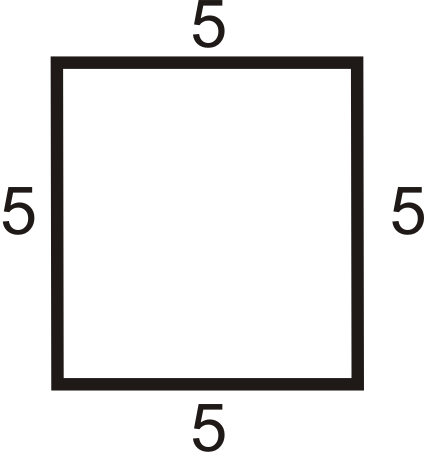
Figura\(\PageIndex{13}\) -
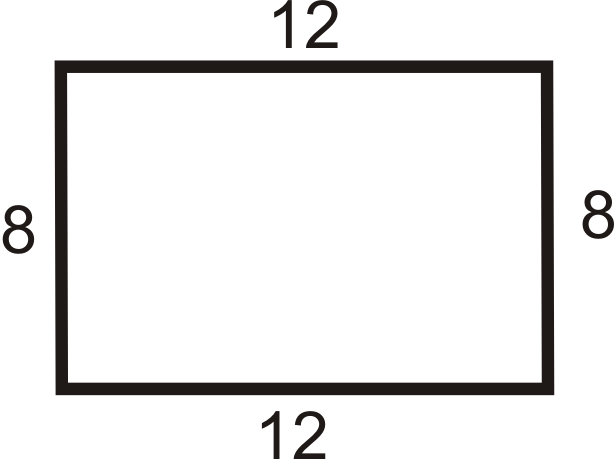
Figura\(\PageIndex{14}\) -
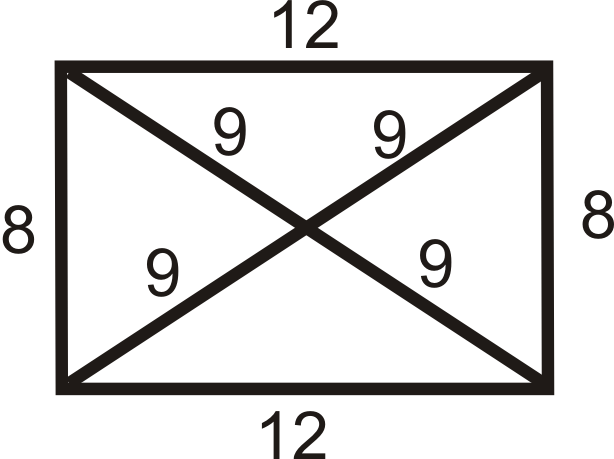
Figura\(\PageIndex{15}\) -
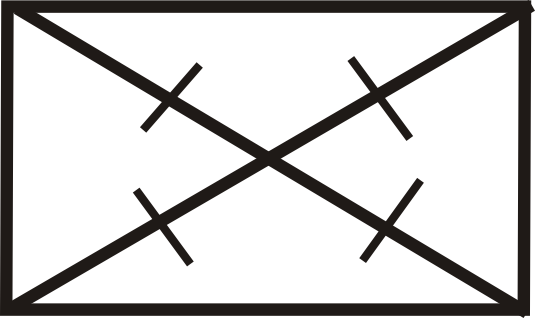
Figura\(\PageIndex{16}\) -
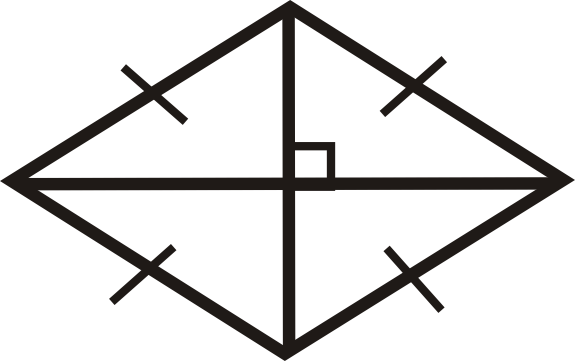
Figura\(\PageIndex{17}\) -
Figura\(\PageIndex{18}\) -
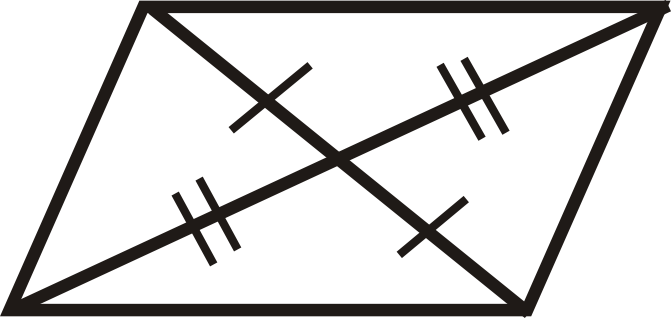
Figura\(\PageIndex{19}\) -
Figura\(\PageIndex{20}\) -
Figura\(\PageIndex{21}\) -
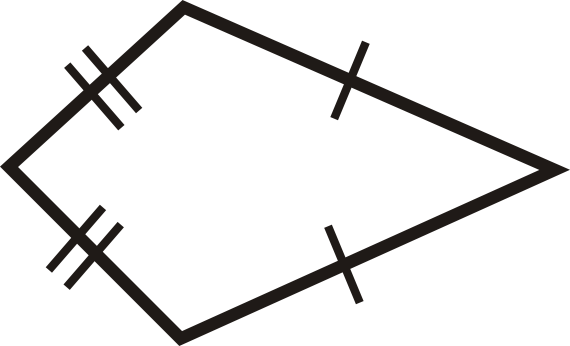
Figura\(\PageIndex{22}\) -
Figura\(\PageIndex{23}\) -
Figura\(\PageIndex{24}\)
Para las preguntas 16-19 determinar si las siguientes son SIEMPRE, ALGUNAS MOMBRAS o NUNCA Explica tu razonamiento.
- Un rectángulo es un rombo.
- Un cuadrado es un paralelogramo.
- Un paralelogramo es regular.
- Un cuadrado es un rectángulo.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.5.
vocabulario
| Término | Definición |
|---|---|
| rectángulo | Un paralelogramo es un rectángulo si y solo si tiene cuatro ángulos rectos (congruentes) |
| rombo | Un paralelogramo es un rombo si y solo si tiene cuatro lados congruentes |
| cuadrado | Un paralelogramo es un cuadrado si y sólo si tiene cuatro ángulos rectos y cuatro lados congruentes. |
| converse | Si una declaración condicional es\(p\rightarrow q\) (si\(p\), entonces\(q\)), entonces lo contrario es\(q\rightarrow p\) (si\(q\), entonces\(p\). Tenga en cuenta que lo contrario de una declaración no es cierto solo porque la declaración original es verdadera. |
| Paralelogramo | Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. |
| Propiedad reflexiva de congruencia | \(\overline{AB}\cong \overline{AB}\)o\(\angle B\cong \angle B\) |
Recursos adicionales
Elemento interactivo
Video: Clasificación de Paralelogramos Principios - Básico
Actividades: Clasificación de paralelogramo Preguntas de discusión
Ayudas de estudio: Guía de estudio de paralelogramos
Práctica: Clasificación de paralelogramos
Mundo Real: Paralelogramos