5.22: Área y Perímetro de Polígonos Similares
- Page ID
- 107525
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La relación de las áreas es el cuadrado del factor de escala; la relación de perímetros es el factor de escala.
Los polígonos son similares cuando sus ángulos correspondientes son iguales y sus lados correspondientes están en la misma proporción. Así como sus lados correspondientes están en la misma proporción, perímetros y áreas de polígonos similares tienen una relación especial.
Perímetros: La relación de los perímetros es la misma que la del factor de escala. De hecho, la relación de cualquier parte de dos formas similares (diagonales, medianas, segmentos medios, altitudes, etc.) es la misma que el factor de escala.
Áreas: Si el factor de escala de los lados de dos polígonos similares es\(\dfrac{m}{n}\), entonces la relación de las áreas es\(\left(\dfrac{m}{n}\right)^2\) (Teorema de Área de Polígonos Similares). Se cuadra la relación porque el área es una medida bidimensional.
¿Y si te dieran dos triángulos similares y te dijeran cuál era el factor de escala de sus lados? ¿Cómo podría encontrar la relación de sus perímetros y la proporción de sus áreas?
Ejemplo\(\PageIndex{1}\)
Los dos rectángulos de abajo son similares. Encuentra el factor de escala y la relación de los perímetros y verifica que los dos resultados sean iguales.
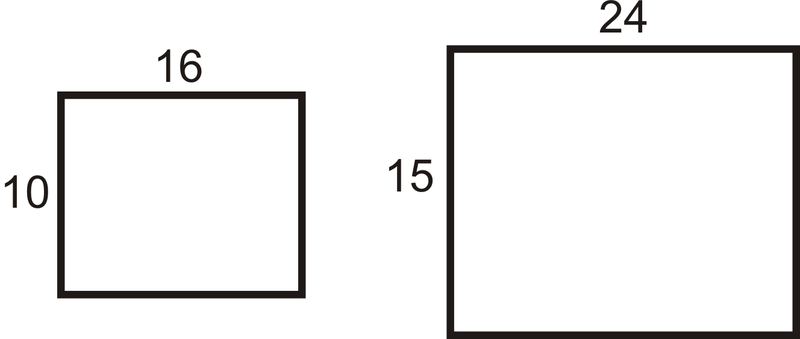
Solución
El factor de escala es\(\dfrac{16}{24}=\dfrac{2}{3}\).
\(\begin{aligned}P_{\text{ small}}=2(10)+2(16)=52\text{ units }\\ P_{\text{ large}}=2(15)+2(24)=78\text{ units }\end{aligned}\)
La relación de los perímetros es\(\dfrac{52}{78}=\dfrac{2}{3}\).
Ejemplo\(\PageIndex{2}\)
Encuentra el área de cada rectángulo del Ejemplo 1. Después, encuentra la proporción de las áreas y verifica que se ajuste al Teorema de Área de Polígonos Similares.
Solución
\(\begin{aligned} A_{\text{ small}}&=10\cdot 16=160\text{ units}^2 \\ A_{\text{ large}}&=15\cdot 24=360\text{ units}^2 \end{aligned}\)
La proporción de las áreas sería\(\dfrac{160}{360}=\dfrac{4}{9}\).
La relación de los lados, o factor de escala es\(\dfrac{2}{3}\) y la proporción de las áreas es\(\dfrac{4}{9}\). Observe que la relación de las áreas es el cuadrado del factor de escala.
Ejemplo\(\PageIndex{3}\)
Encuentra la proporción de las áreas del rombo a continuación. Los rombos son similares.
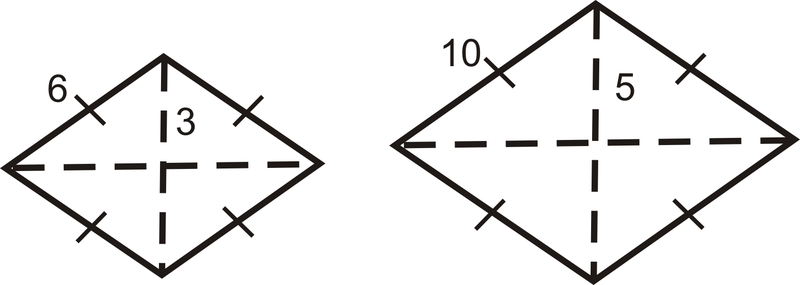
Solución
Encuentra la relación de los lados y cuadrázala.
\(\left(\dfrac{3}{5}\right)^2=\dfrac{9}{25}\)
Ejemplo\(\PageIndex{4}\)
Dos trapecios son similares. Si el factor de escala es 34 y el área del trapecio más pequeño es\(81\text{ cm }^2\), ¿cuál es el área del trapecio más grande?
Solución
En primer lugar, la proporción de las áreas es\(\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16}\). Ahora, necesitamos el área del trapecio más grande. Para encontrar esto, establezca una proporción usando la proporción de área.
\(\begin{aligned}\dfrac{9}{16}=\dfrac{81}{A} \rightarrow 9A&=1296 \\ A&=144\text{ cm }^2 \end{aligned}\)
Ejemplo\(\PageIndex{5}\)
Dos triángulos son similares. La proporción de las áreas es\(\dfrac{25}{64}\). ¿Cuál es el factor de escala?
Solución
El factor de escala es\(\sqrt{\dfrac{25}{64}}=\dfrac{5}{8}\).
Ejemplo\(\PageIndex{6}\)
Usando las proporciones del Ejemplo 5, encuentra la longitud de la base del triángulo más pequeño si la longitud de la base del triángulo más grande es de 24 unidades.
Solución
Configura una proporción usando el factor de escala.
\(\begin{aligned}\dfrac{5}{8}=\dfrac{b}{24} \rightarrow 8b&=120 \\ b&=15\text{ units } \end{aligned}\)
Revisar
Determinar la relación de las áreas, dada la relación de los lados de un polígono.
- \(\dfrac{3}{5}\)
- \(\dfrac{1}{4}\)
- \(\dfrac{7}{2}\)
- \(\dfrac{6}{11}\)
Determinar la relación de los lados de un polígono, dada la proporción de las áreas.
- \(\dfrac{1}{36}\)
- \(\dfrac{4}{81}\)
- \(\dfrac{49}{9}\)
- \(\dfrac{25}{144}\)
Se trata de un triángulo equilátero conformado por 4 triángulos equiláteros congruentes.
- ¿Cuál es la relación entre las áreas del triángulo grande y uno de los triángulos pequeños?
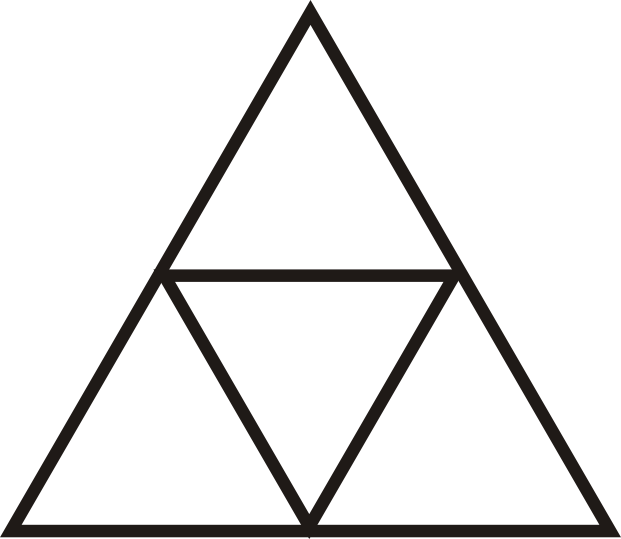
Figura\(\PageIndex{4}\) - ¿Cuál es el factor de escala del triángulo grande a pequeño?
- Si el área del triángulo grande es\(20\text{ units }^2\), ¿cuál es el área de un triángulo pequeño?
- Si la longitud de la altitud de un triángulo pequeño es\(2\sqrt{3}\), encuentra el perímetro del triángulo grande.

Figura\(\PageIndex{5}\) - Encuentra el perímetro de la plaza grande y la plaza azul.
- Encuentra el factor de escala del cuadrado azul y el cuadrado grande.
- Encuentra la proporción de sus perímetros.
- Encuentra el área de los cuadrados azules y grandes.
- Encuentra la proporción de sus áreas.
- Encuentra la longitud de las diagonales de los cuadrados azules y grandes. Póngalos en una proporción. ¿Cuál es esta la misma proporción que?
- Dos rectángulos son similares con un factor de escala de\(\dfrac{4}{7}\). Si el área del rectángulo más grande es\(294\text{ in }^2\), busque el área del rectángulo más pequeño.
- Dos triángulos son similares con un factor de escala de\(\dfrac{1}{3}\). Si el área del triángulo más pequeño es\(22\text{ ft }^2\), busque el área del triángulo más grande.
- La relación de las áreas de dos cuadrados similares es\(\dfrac{16}{81}\). Si la longitud de un lado del cuadrado más pequeño es de 24 unidades, encuentra la longitud de un lado en el cuadrado más grande.
- La relación de las áreas de dos triángulos rectos es\(\dfrac{4}{9}\). Si la longitud de la hipotenusa del triángulo más grande es de 48 unidades, encuentra la longitud de la hipotenusa del triángulo más pequeño.
Las preguntas 23-26 se construyen unas de otras. Puede suponer que los problemas están conectados.
- Dos rombos similares tienen áreas de\(72\text{ units }^2\) y\(162\text{ units }^2\). Encuentra la proporción de las áreas.
- Encuentra el factor de escala.
- Las diagonales en estos rombos son congruentes. Encuentra la longitud de las diagonales y los costados.
- ¿Qué tipo de rombos son estos cuadriláteros?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.7.
El vocabulario
| Término | Definición |
|---|---|
| zona | La cantidad de espacio dentro de una figura. El área se mide en unidades cuadradas. |
| Perimetral | El perímetro es la distancia alrededor de una figura bidimensional. |
| Proporción | Una proporción es una ecuación que muestra dos proporciones equivalentes. |
| Ratio | Una relación es una comparación de dos cantidades que se pueden escribir en forma de fracción, con dos puntos o con la palabra “a”. |
| Factor de Escala | Un factor de escala es una relación entre la escala y la dimensión original o real escrita en la forma más simple. |
| Trapecio | Un trapecio es un cuadrilátero con exactamente un par de lados opuestos paralelos. |
Recursos adicionales
Elemento Interactivo
Video: Área y Perímetro de Polígonos Similares Principios - Básicos
Actividades: Área y Perímetro de Polígonos Similares
Ayudas de estudio: Guía de estudio de perímetro y área
Mundo real: En la casa de muñecas

