5.21: Área de Polígonos Regulares e Irregulares
- Page ID
- 107488
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La mitad del apotema multiplicado por el perímetro.
Área de Polígonos Regulares
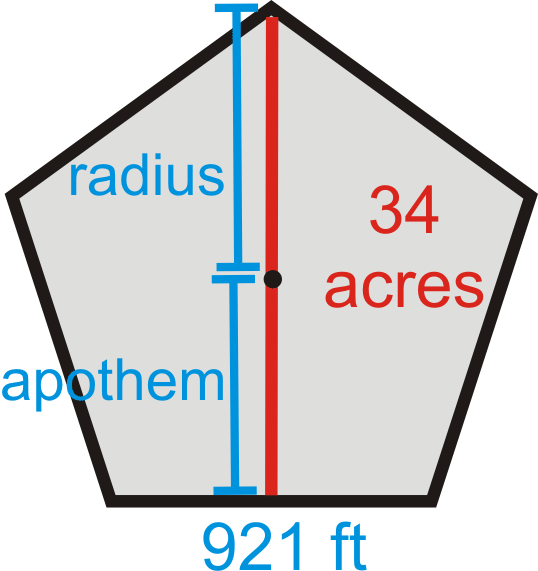
¿Y si te pidieran encontrar la distancia a través de El Pentágono en Arlington, VA? El Pentágono, que también alberga el Departamento de Defensa, está integrado por dos pentágonos regulares con el mismo centro. Toda el área del edificio es de 29 acres (40,000 pies cuadrados en un acre), con un patio adicional de 5 acres en el centro. La longitud de cada pared exterior es de 921 pies. ¿Cuál es la distancia total a través del pentágono? Redondea tu respuesta a la centésima más cercana.

Un polígono regular es un polígono con lados y ángulos congruentes. Recordemos que el perímetro de un cuadrado es 4 veces la longitud de un lado porque cada lado es congruente. Podemos extender este concepto a cualquier polígono regular.
Perímetro de un Polígono Regular: Si la longitud de un lado es s y hay\(n\) lados en un polígono regular, entonces el perímetro es\(P=ns\).
Para encontrar el área de un polígono regular, necesitamos definir alguna terminología nueva. Primero, todos los polígonos regulares se pueden inscribir en un círculo. Entonces, los polígonos regulares tienen un centro y un radio, que son el centro y el radio del círculo circunscrito. También como un círculo, un polígono regular tendrá un ángulo central formado. En un polígono regular, sin embargo, el ángulo central es el ángulo formado por dos radios dibujados a vértices consecutivos del polígono. En la imagen de abajo, el ángulo central es\(\angle BAD\). También, fíjese que\(\Delta BAD\) es un triángulo isósceles. Cada polígono regular con n lados está formado por n triángulos isósceles. La altura de estos triángulos isósceles se llama apotema.
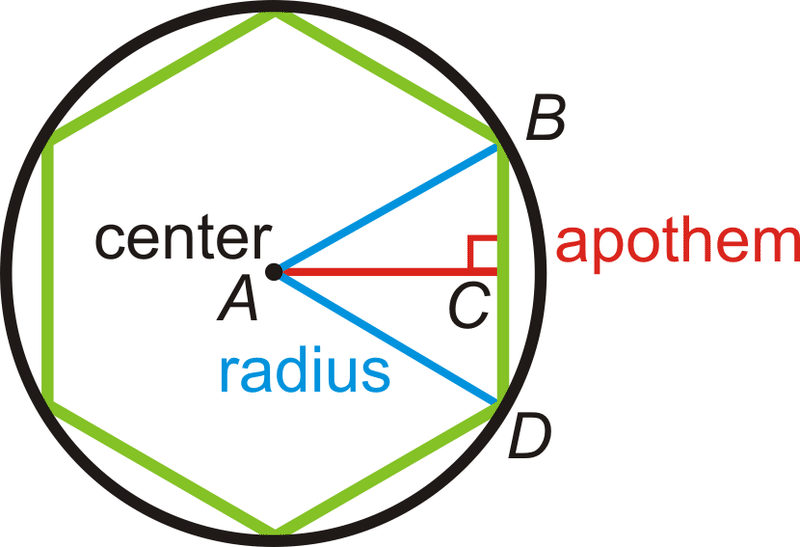
El área de cada triángulo es\(A_{\Delta} =\dfrac{1}{2}bh=\dfrac{1}{2}sa\), donde s es la longitud de un lado y a es el apotema. Si hay n lados en el polígono regular, entonces se compone de n triángulos congruentes.
Área de un Polígono Regular: Si hay n lados con longitud s en un polígono regular y a es el apotema, entonces\(A=\dfrac{1}{2}asn\) o\(A=\dfrac{1}{2}aP\), donde\(P\) está el perímetro.
Cálculo del perímetro
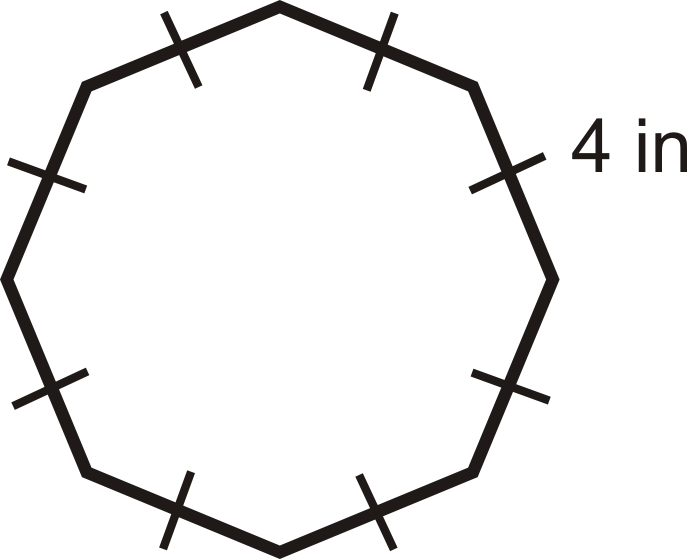
¿Cuál es el perímetro de un octágono regular con lados de 4 pulgadas?
Si cada lado es de 4 pulgadas y hay 8 lados, eso significa que el perímetro es\(8(4\text{ in }) = 32\text{ inches }\).
Encontrar longitudes laterales
El perímetro de un heptágono regular es de 35 cm. ¿Cuál es la longitud de cada lado?
Si\(P=ns\), entonces\(35\text{ cm }=7s\). Por lo tanto,\(s=5\text{ cm }\).
Encontrar la longitud del Apotema
Encuentra la longitud del apotema en el octágono regular. Redondea tu respuesta a la centésima más cercana.
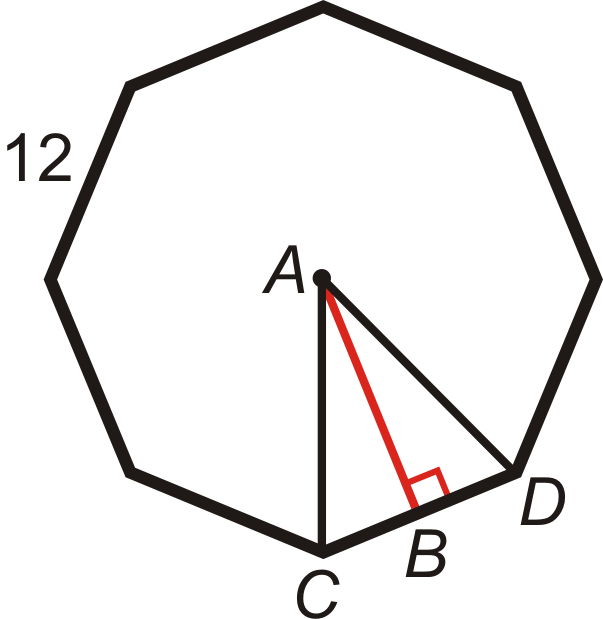
Para encontrar la longitud del apotema, AB, necesitarás usar las proporciones trigonométricas. Primero, encuentra\(m\angle CAD\). Hay\(360^{\circ}\) alrededor de un punto, entonces\(m\angle CAD=\dfrac{360^{\circ}}{8}=45^{\circ}\). Ahora, podemos usar esto para encontrar los otros dos ángulos en\(\Delta CAD\). m\ ángulo ACB\) y m\ ángulo ADC\) son iguales porque\ Delta CAD\) es un triángulo rectángulo.
\(\begin{aligned}m\angle CAD+m\angle ACB+m\angle ADC&=180^{\circ} \\ 45^{\circ}+2m\angle ACB&=180^{\circ} \\ 2m\angle ACB&=135^{\circ} \\ m\angle ACB&=67.5^{\circ}\end{aligned}\)
Para encontrar AB, debemos usar la relación tangente. Se puede utilizar cualquiera de los dos ángulos agudos.
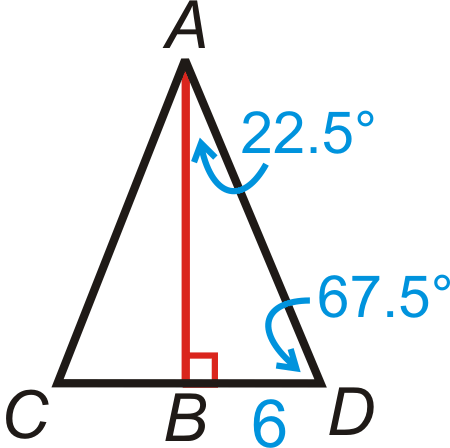
\(\begin{aligned}tan67.5^{\circ}&=\dfrac{AB}{6} \\ AB&=6\cdot tan67.5^{\circ}\approx 14.49\end{aligned}\)
Problema del Pentágono revisado
De la imagen de abajo, podemos ver que la distancia total a través del Pentágono es la longitud del apotema más la longitud del radio. Si el área total del Pentágono es de 34 acres, es decir 2,720,000 pies cuadrados. Por lo tanto, la ecuación de área es\(2720000=\dfrac{1}{2}a(921)(5)\) y el apotema es 590.66 pies. Para encontrar el radio, podemos usar el Teorema de Pitágoras, con el apotema y la mitad de la longitud de un lado o la relación sinusoidal. Recordemos del Ejemplo 5, que cada ángulo central en un pentágono es\(72^{\circ}\), así que usaríamos la mitad de eso para el triángulo rectángulo.
\(sin36^{\circ}=\dfrac{460.5}{r} \rightarrow r=\dfrac{460.5}{sin36^{\circ}}\approx 783.45\text{ ft }\)
Por lo tanto, la distancia total a través es\(590.66+783.45=1374.11\: ft\).
Ejemplo\(\PageIndex{1}\)
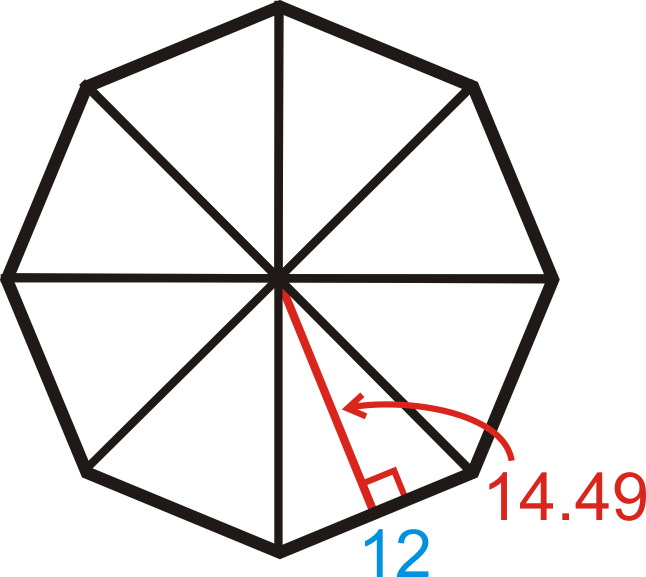
Encuentra el área del octágono regular en el Ejemplo C.
Solución
El octágono se puede dividir en 8 triángulos congruentes. Entonces, si encontramos el área de un triángulo y la multiplicamos por 8, tendremos el área de todo el octágono.
\(A_{octagon}=8(12\cdot 12\cdot 14.49)=695.52 units^2\)
Ejemplo\(\PageIndex{2}\)
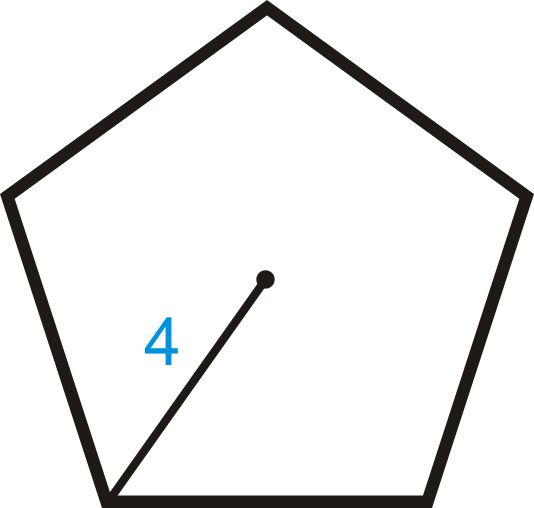
Encuentra el área del polígono regular con radio 4.
Solución
INSERTB En este problema necesitamos encontrar el apotema y la longitud del lado antes de poder encontrar el área de todo el polígono. Cada ángulo central para un pentágono regular es\(\dfrac{360^{\circ}}{5}=72^{\circ}\). Entonces, la mitad de eso, hacer un triángulo rectángulo con el apotema, es\(36^{\circ}\). Necesitamos usar seno y coseno.
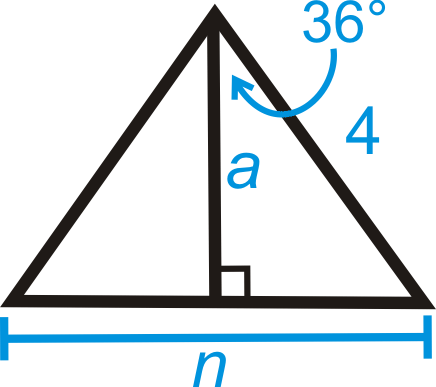
\ (\ begin {array} {rlr}
\ sin 36^ {\ circ} & =\ frac {.5 n} {4} &\ cos 36^ {\ circ} &=\ frac {a} {4}\
4\ sin 36^ {\ circ} & =\ frac {1} {2} n & 4\ cos 36^ {\ circ} &=a\
8\ sin 36^ {\ circ} & =n & a &\ aprox 3.24\\
n &\ aprox 4.7
\ end {array}\)
Usando estas dos piezas de información, ahora podemos encontrar la zona. \(A=12(3.24)(5)(4.7)\approx 38.07 units^2\).
Ejemplo\(\PageIndex{3}\)
El área de un hexágono regular es\(54\sqrt{3}\) y el perímetro es 36. Encuentra la longitud de los costados y el apotema.
Solución
Enchufa lo que sabes tanto en el área como en las fórmulas perimetrales para resolver por la longitud de un lado y el apotema.
\ (\ begin {array} {rlrl}
P&=s n & A & =\ frac {1} {2} a P\\
36&=6 s & 54\ sqrt {3} & =\ frac {1} {2} a (36)\\
s&=6 & 54\ sqrt {3} & =18 a\\
3\ sqrt {3} &=a
\ end {matriz}\)
Revisar
Utilice el hexágono regular a continuación para responder las siguientes preguntas. Cada lado mide 10 cm de largo.
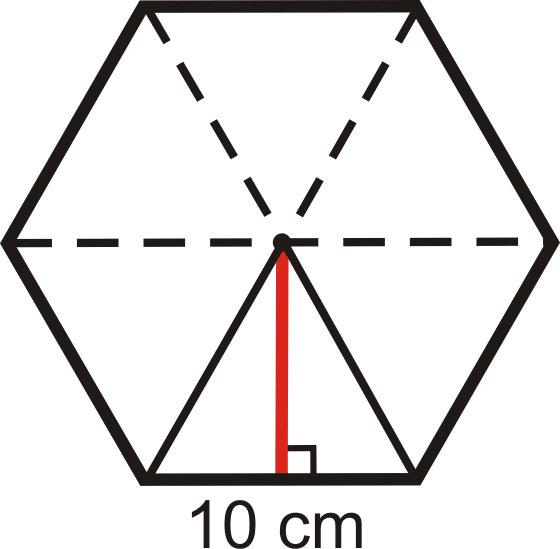
- Cada segmento de línea discontinua es un (n) ________________.
- El segmento de línea roja es a (n) __________________.
- Hay _____ triángulos congruentes en un hexágono regular.
- En un hexágono regular, todos los triángulos son _________________.
- Encuentra el radio de este hexágono.
- Encuentra el apotema.
- Encuentra el perímetro.
- Encuentra la zona.
Encuentra el área y perímetro de cada uno de los siguientes polígonos regulares. Redondea tu respuesta a la centésima más cercana.
-
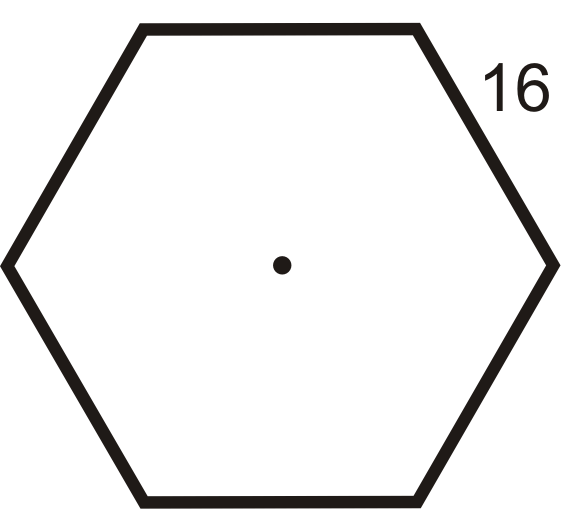
Figura\(\PageIndex{11}\) -
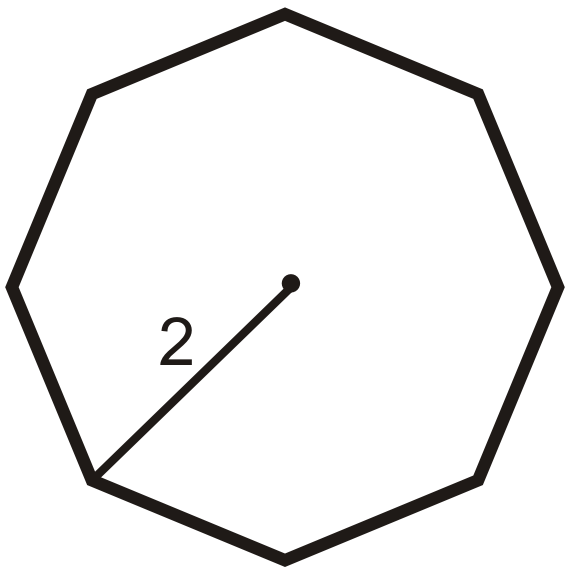
Figura\(\PageIndex{12}\) -
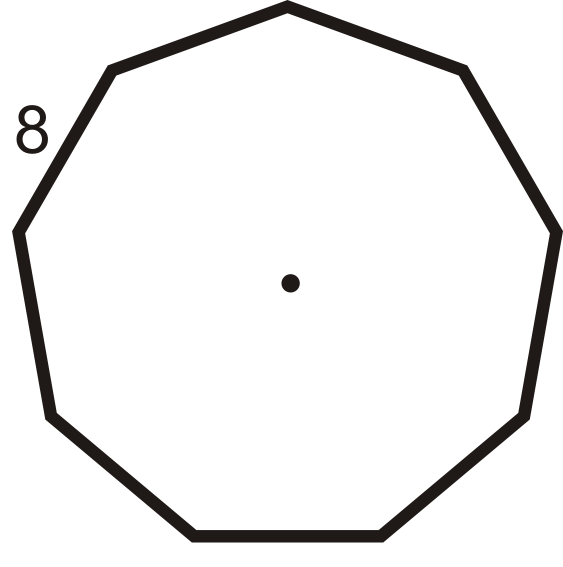
Figura\(\PageIndex{13}\) -
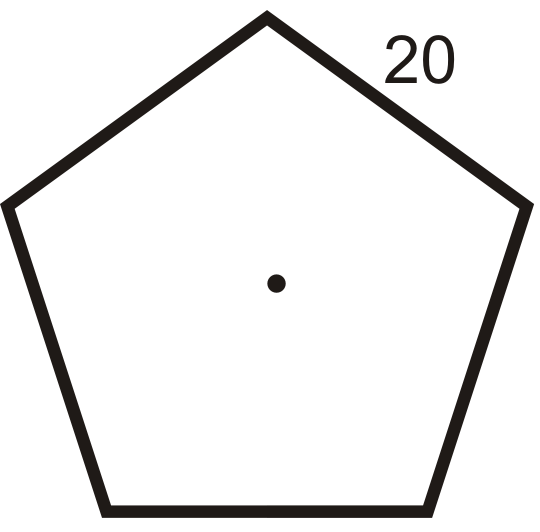
Figura\(\PageIndex{14}\) - Si el perímetro de un decágono regular es 65, ¿cuál es la longitud de cada lado?
- Un polígono regular tiene un perímetro de 132 y los lados tienen 11 unidades de largo. ¿Cuántos lados tiene el polígono?
- El área de un pentágono regular es\(440.44\text{ in }^2\) y el perímetro es de 80 pulgadas. Encuentra la longitud del apotema del pentágono.
- El área de un octágono regular es\(695.3\text{ cm }^2\) y los lados son de 12 cm. ¿Cuál es la longitud del apotema?
Un regular de 20 gones y uno regular de 40 gones se inscriben en un círculo con un radio de 15 unidades.
- Desafío Derivar una fórmula para el área de un hexágono regular con lados de longitud s. Su única variable será s. SUGERENCIA: Use relaciones triangulares 30-60-90.
- Desafía en los siguientes pasos derivarás una fórmula alternativa para encontrar el área de un polígono regular con n lados.
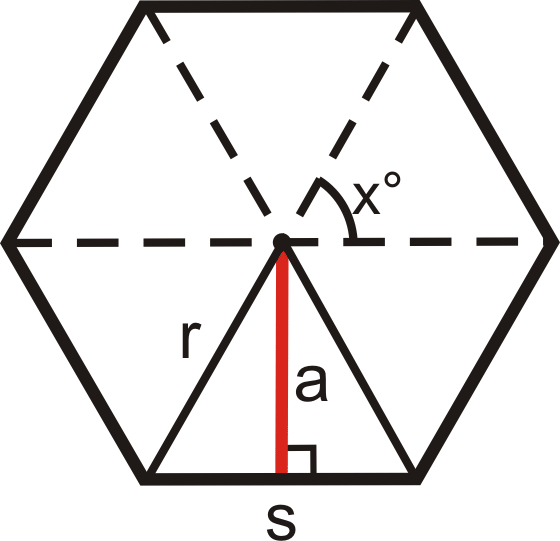
Vamos a comenzar pensando en un polígono con n lados como n triángulos isósceles congruentes. Encontraremos la suma de las áreas de estos triángulos mediante trigonometría. Primero, el área de un triángulo es\(\dfrac{1}{2}bh\). En el diagrama de la derecha, esta fórmula de área sería\(\dfrac{1}{2}sa\), donde s es la longitud de un lado y a es la longitud del apotema. En el diagrama,\(x\) representa la medida del ángulo de vértice de cada triángulo isósceles.
- El apotema, a, divide el triángulo en dos triángulos rectos congruentes. El ángulo superior en cada uno es\(\dfrac{x^{\circ}}{2}\). Encontrar\(sin(\dfrac{x^{\circ}}{2})\) y\(cos(\dfrac{x^{\circ}}{2})\).
- Resuelve tu ecuación de pecado para encontrar una expresión para s en términos de\(r\) y\(x\).
- Resuelve tu ecuación cos para encontrar una expresión para a en términos de\(r\) y\(x\).
- Sustituir estas expresiones en la ecuación para el área de uno de los triángulos,\ dfrac {1} {2} sa\).
- Como habrá n triángulos en un n-gon, necesitas multiplicar tu expresión de la parte d por n para obtener el área total.
- ¿Cómo le dirías a alguien que encuentre el valor de\(x\) para un n-gon regular?
Usa la fórmula que derivaste en el problema 18 para encontrar el área de los polígonos regulares descritos en los problemas 19-22. Redondea tus respuestas a la centésima más cercana.
- Decagon con radio 12 cm.
- 20 gones con radio de 5 in.
- 15 gones con radio de longitud 8 cm.
- 45 gones con radio de longitud 7 in.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.12.
Recursos adicionales
Elemento interactivo
Video: Área de Polígonos Regulares Principios
Práctica: Área de Polígonos Regulares e Irregulares

