6.2: Identificar componentes de círculo
- Page ID
- 107304
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Componentes, circunferencia y área de círculos.
Partes de Círculos
Círculos
Un círculo es el conjunto de todos los puntos del plano que están a la misma distancia de un punto específico, llamado centro. El centro del círculo de abajo es el punto A. A este círculo lo llamamos “círculo A”, y está etiquetado\(\bigodot A\).
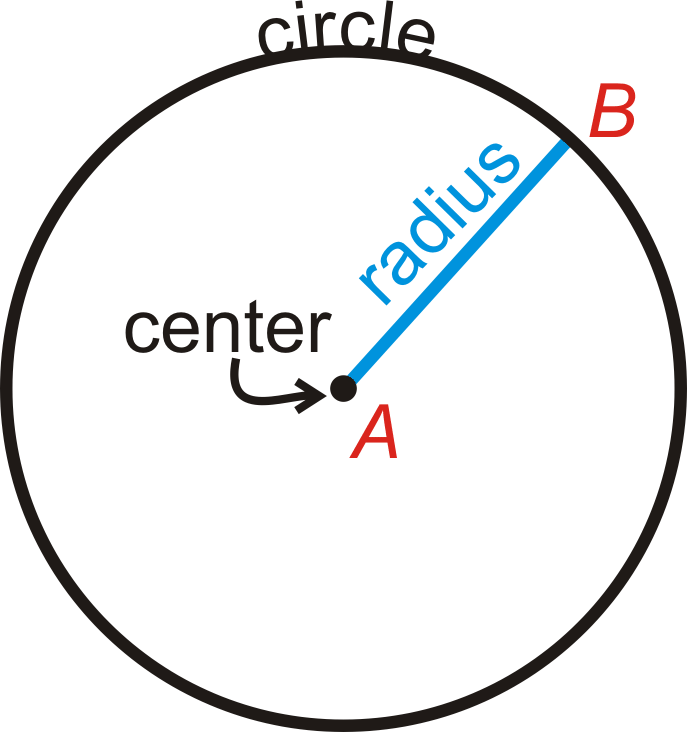
Partes Circulares Importantes
Radio: La distancia desde el centro del círculo hasta su borde exterior.
Acorde: Un segmento de línea cuyos extremos están en un círculo.
Diámetro: Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio.
Secante: Una línea que cruza un círculo en dos puntos.
Tangente: Una línea que cruza un círculo exactamente en un punto.
Punto de tangencia: El punto donde una línea tangente toca el círculo.
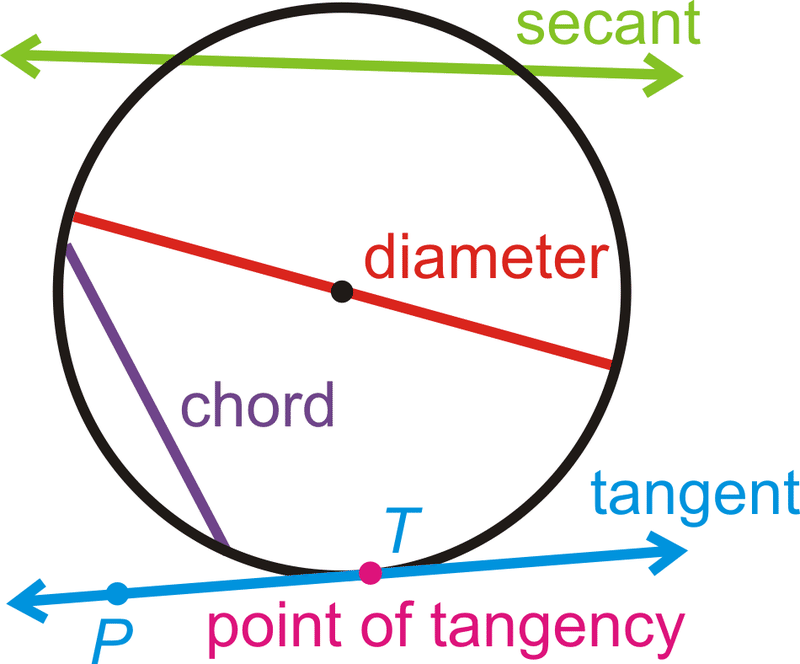
El rayo tangente\(\overrightarrow{TP}\) y el segmento\(\overline{TP}\) tangente también se denominan tangentes.
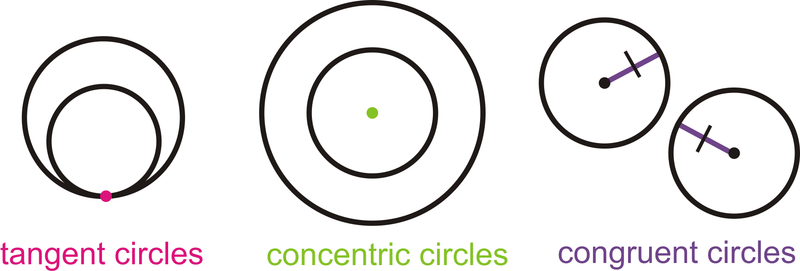
Círculos tangentes: Dos o más círculos que se cruzan en un punto.
Círculos concéntricos: Dos o más círculos que tienen el mismo centro, pero radios diferentes.
Círculos congruentes: Dos o más círculos con el mismo radio, pero diferente centro
¿Y si trazas una línea a través de un círculo de un lado a otro que no pasa por el centro? ¿Y si dibujaste una línea fuera de un círculo que tocó el círculo en un punto? ¿Cómo llamarías a estas líneas que dibujaste?
Ejemplo\(\PageIndex{1}\)
Encuentra las partes\(\bigodot A\) que mejor se ajusten a cada descripción.
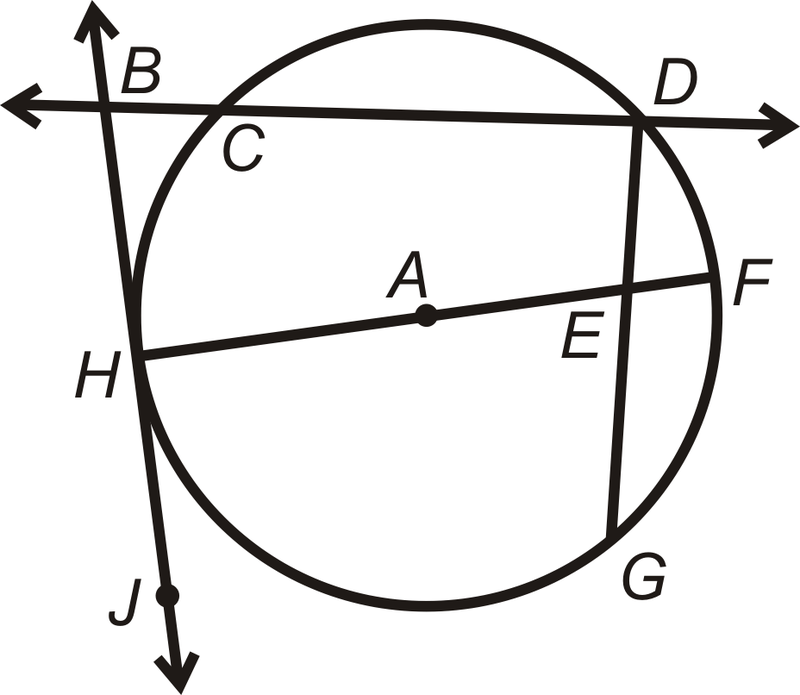
- Un radio
- Un acorde
- Una línea tangente
- Un punto de tangencia
- Un diámetro
- Una secante
Solución
- \ overline {HA}\) o\ overline {AF}\)
- \(\overline{CD}\)\(\overline{HF}\), o\ overline {DG}\)
- \(\overleftrightarrow{BJ}\)
- \(Point H\)
- \(\overline{HF}\)
- \(\overleftrightarrow{BD}\)
Ejemplo\(\PageIndex{2}\)
Dibuja un ejemplo de cómo dos círculos pueden intersectarse sin ninguno, uno y dos puntos de intersección. Harás tres dibujos separados.
Solución
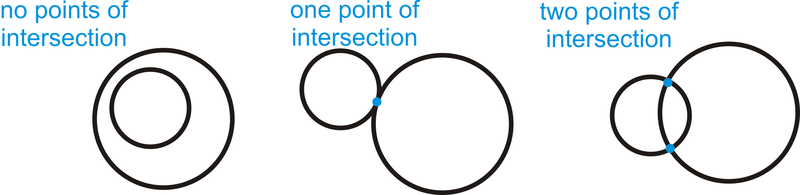
Ejemplo\(\PageIndex{3}\)
Determinar si alguno de los siguientes círculos es congruente.
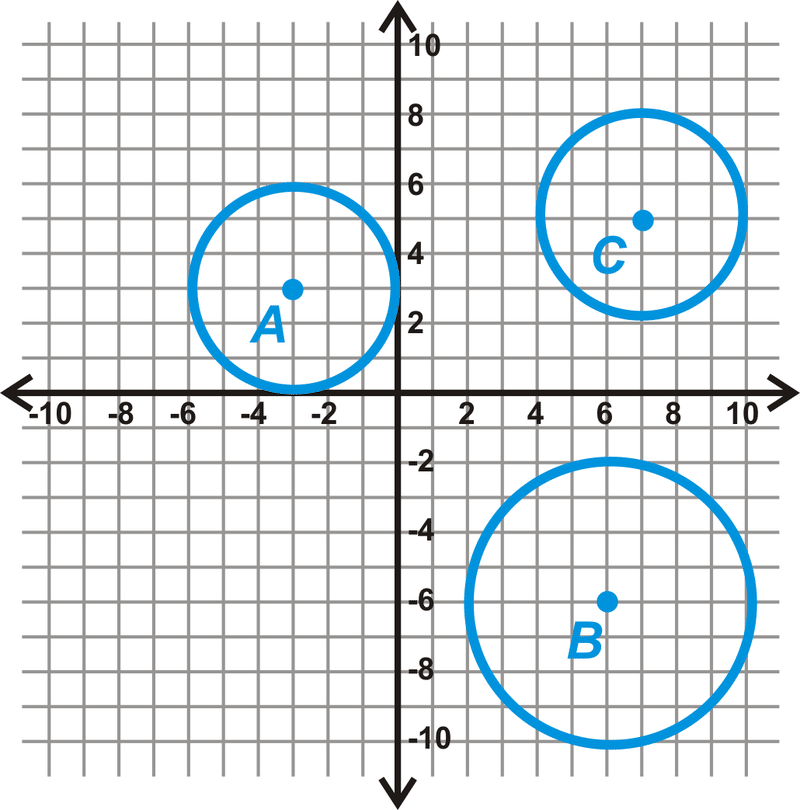
Solución
Desde cada centro, cuente las unidades hasta el borde exterior del círculo. Es más fácil contar vertical u horizontalmente. Haciendo esto, tenemos:
\(\begin{aligned} \text{Radius of } \bigodot A&=3\text{ unit } \\ \text{Radius of } \bigodot B&=4\text{ unit }\\ \text{Radius of } \bigodot C&=3\text{ unit }\end{aligned} \)
A partir de estas mediciones, vemos eso\(\bigodot A\cong \bigodot C\).
Observe que los círculos son congruentes. Las longitudes de los radios son iguales.
Ejemplo\(\PageIndex{4}\)
¿Es posible tener una línea que intersecta un círculo tres veces? Si es así, dibuja uno. Si no, explique.
Solución
No es posible. Por definición, todas las líneas son rectas. El número máximo de veces que una línea puede intersectar un círculo es dos veces.
Ejemplo\(\PageIndex{5}\)
¿Todos los círculos son similares?
Solución
Sí. Todos los círculos tienen la misma forma, pero no necesariamente del mismo tamaño, por lo que son similares.
Revisar
Determinar qué término describe mejor cada una de las siguientes partes de\(\bigodot P\).
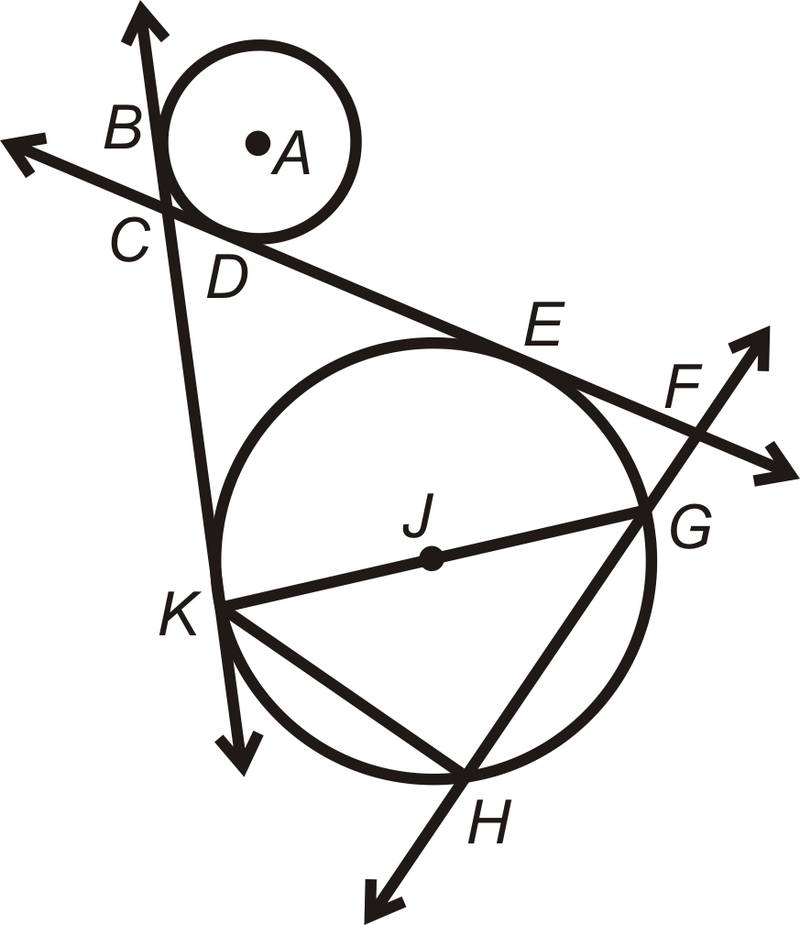
- \(\overline{KG}\)
- \(\overleftrightarrow{FH}\)
- \(\overline{FH}\)
- \(E\)
- \(\overleftrightarrow{BK}\)
- \(\overleftrightarrow{CF}\)
- \(A\)
- \(\overline{JG}\)
- ¿Cuál es el acorde más largo de cualquier círculo?
Utilice la gráfica a continuación para responder a las siguientes preguntas.
- Encuentra el radio de cada círculo.
- ¿Algún círculo es congruente? ¿Cómo lo sabes?
- Encuentra todas las tangentes comunes para\(\bigodot B\) y\(\bigodot C\).
- \(\bigodot C\)y\(\bigodot E\) son externamente tangentes. ¿Qué es\(CE\)?
- Encuentra la ecuación de\(\overline{CE}\).
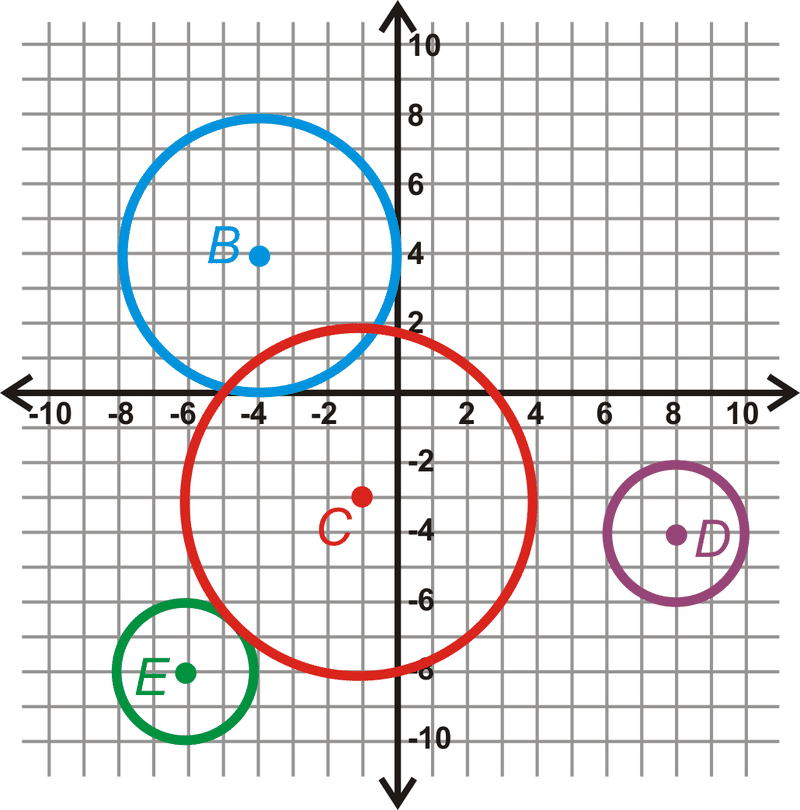
Recursos
El vocabulario
| Término | Definición |
|---|---|
| acorde | Un segmento de línea cuyos extremos están en un círculo. |
| Círculo | Un círculo es el conjunto de todos los puntos a una distancia específica de un punto dado en dos dimensiones. |
| círculos concéntricos | Dos o más círculos que tienen el mismo centro, pero radios diferentes. |
| círculos congruentes | Dos o más círculos con el mismo radio, pero diferentes centros. |
| Diámetro | El diámetro es la medida de la distancia a través del centro de un círculo. El diámetro es igual al doble de la medida del radio. |
| punto de tangencia | El punto donde la línea tangente toca el círculo. |
| Radio | El radio de un círculo es la distancia desde el centro del círculo hasta el borde del círculo. |
| Circunferencia | La circunferencia de un círculo es la medida de la distancia alrededor del borde exterior de un círculo. |
| Secante | La secante de un ángulo en un triángulo rectángulo es el valor que se encuentra dividiendo la longitud de la hipotenusa por la longitud del lado adyacente al ángulo dado. La relación secante es la recíproca de la relación coseno. |
| Tangente | La tangente de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud del lado adyacente al ángulo dado. |
| Círculos tangentes | Los Círculos Tangentes son dos o más círculos que se cruzan en un punto. |
Recursos adicionales
Elemento Interactivo
Video: Introducción a los Círculos
Actividades: Partes de Círculos Preguntas de Discusión
Ayudas de estudio: Propiedades de una guía de estudio circular
Práctica: Identificar componentes de círculo
Mundo real: Una rotonda de camino a casa

