6.3: Usar Diámetro, Radio y Pi
- Page ID
- 107279
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Identificar la relación constante\(\pi= \dfrac{C}{d}\).
Pi

Carla tiene que ir a la tienda y conseguir un mantel para la mesa redonda en el comedor. Para obtener el mantel del tamaño correcto, necesita saber la distancia de un lado de la mesa al otro lado. El criterio de 3 pies de largo que tiene solo puede medir hasta el centro de la mesa, o a mitad de camino. ¿Cómo puede Carla averiguar la distancia a través de la mesa circular con solo el criterio y luego usar esa información para averiguar la circunferencia de la mesa?
En este concepto, aprenderás la relación entre diámetro y radio e identificarás pi como la relación de diámetro a circunferencia en un círculo.
Relaciones de círculo
Para trabajar con círculos, es necesario conocer las diferentes partes de un círculo y cómo se miden estas partes clave.
Se puede medir la distancia a través del centro del círculo. Esta distancia se llama el diámetro del círculo.
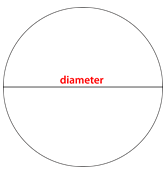
Se puede medir la distancia desde el centro del círculo hasta el borde exterior. Esta distancia se llama el radio.
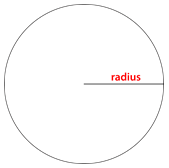
Observe que el radio es la mitad de la medida del diámetro.
También se puede medir el perímetro del círculo. Esta distancia se llama la circunferencia del círculo.
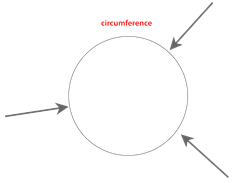
A Arquímedes, matemático de la antigua Grecia, se le atribuye haber averiguado la relación entre el diámetro y la circunferencia de un círculo. Arquímedes descubrió que si tomas la distancia a través del círculo (diámetro) y lo estiras alrededor de la circunferencia, tomaría un poco más de 3 longitudes del diámetro para rodear la circunferencia del círculo.
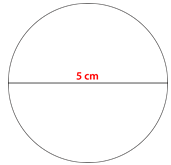
Digamos que el diámetro de este círculo es de 5 cm, en ese caso la circunferencia del círculo es de tres y un poco más veces los 5 cm, o un poco menos de 16 cm.
La relación entre el diámetro y la circunferencia se llama pi,\(\pi\). El valor numérico de pi es un decimal no terminante, lo que significa que no puede escribirse precisamente como un numeral ya que los decimales nunca terminan ni forman un patrón. Entonces, el número 3.14 se usa para representar pi y se usa para estimar la circunferencia de un círculo.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Carla y su problema de medir el diámetro de la mesa redonda.
Carla seguía debatiendo cómo encontrar el diámetro de la mesa redonda cuando su madre caminaba por el comedor. Cuando Carla le explicó el problema a su mamá, su mamá le dijo si la vara de medir de 3 pies de largo medía la distancia desde el borde de la mesa hasta el punto central, entonces ese era el radio de la mesa. Sabiendo que el radio de la mesa era de 3 pies, Carla sabía que podía usar la fórmula de relación para radio y diámetro para averiguar la distancia de un lado de la mesa al otro.
Solución
Primero, Carla sustituyó la medida dada en la fórmula por diámetro y radio.
\(\begin{aligned} 2 (\text{ radius })=\text{ diameter } \\ 2 (3\text{ feet })=\text{ diameter }\end{aligned}\)
A continuación, ella multiplicó 2 veces 3.
\(6\text{ feet }= \text{ diameter }\)
El diámetro de la mesa es de 6 pies.
Carla podría usar esta información para averiguar las circunferencias de la tabla multiplicando el diámetro y pi (3.14).
Ejemplo\(\PageIndex{2}\)
Utilice el valor dado para el radio para encontrar el diámetro.
Si el radio de un círculo es 3, ¿cuál es el diámetro?
Solución
Primero, anote la definición de radio y diámetro. El radio es la mitad del diámetro o el diámetro es el doble de la longitud del radio.
\(2 (\text{ radius })=\text{ diameter }\)
A continuación, multiplica el radio por 2 para obtener 6.
\(2(3)=6\)
La respuesta es 6.
Ejemplo\(\PageIndex{3}\)
Si un círculo tiene un diámetro de 14 pulgadas, ¿cuál es su radio?
Solución
Primero, sustituya la medida dada en la fórmula por diámetro y radio.
\(\begin{aligned} 2 (\text{ radius })&=\text{ diameter }\\ 2r&=14 \text{ inches }\end{aligned}\)
A continuación, divida ambos lados por 2.
\(\begin{aligned}\dfrac{2r}{2}&=\dfrac{14}{2} \\ r&=7 \end{aligned}\)
La respuesta es 7.
Ejemplo\(\PageIndex{4}\)
Si un círculo tiene un radio de 11 pulgadas, ¿cuál es su diámetro?
Solución
Primero, sustituya la medida dada en la fórmula por diámetro y radio.
\(\begin{aligned}2(\text{ radius })=\text{ diameter } \\ 2(11\text{ inches })=\text{ diameter } \end{aligned}\)
A continuación, multiplique 2 y 11.
\(22=\text{ diameter }\)
La respuesta es 22.
Ejemplo\(\PageIndex{5}\)
Si un círculo tiene un diámetro de 18 pulgadas, ¿cuál es su radio?
Solución
Primero, sustituir los valores conocidos en la ecuación.
\(2(r)=18\)
A continuación, haga las matemáticas y divida ambos lados por 2.
\(\begin{aligned}\dfrac{2r}{2}&=\dfrac{18}{2} \\ r&=9\end{aligned}\)
La respuesta es 9.
Revisar
Dado cada radio, determinar el diámetro.
- \(r=4\text{ in. }\)
- \(r=6\text{ in. }\)
- \(r=5\text{ in. }\)
- \(r=12\text{ in. }\)
- \(r=16\text{ ft. }\)
- \(r=28\text{ mm. }\)
- \(r=12.5\text{ ft. }\)
- \(r=1.25\text{ m. }\)
Dado cada diámetro, determinar el radio.
- \(d=12\text{ m. }\)
- \(d=18\text{ m. }\)
- \(d=12.5\text{ in. }\)
- \(d=18.5\text{ ft. }\)
- \(d=9.8\text{ in. }\)
- \(d=1.45\text{ mm. }\)
- \(d=1.75\text{ ft. }\)
- \(d=2.5\text{ ft. }\)
- \(d=221.25\text{ m. }\)
El vocabulario
| Término | Definición |
|---|---|
| \ pi | \(\pi\)(Pi) es la relación entre la circunferencia de un círculo y su diámetro. Se trata de un número irracional que es aproximadamente igual a 3.14. |
| Arquímedes | Arquímedes fue un matemático y filósofo griego. Entre muchas otras cosas, identificó a 3.14 como pi. |
| Circunferencia | La circunferencia de un círculo es la medida de la distancia alrededor del borde exterior de un círculo. |
| Diámetro | El diámetro es la medida de la distancia a través del centro de un círculo. El diámetro es igual al doble de la medida del radio. |
| Pi | \(\pi\)(Pi) es la relación entre la circunferencia de un círculo y su diámetro. Se trata de un número irracional que es aproximadamente igual a 3.14. |
| Radio | El radio de un círculo es la distancia desde el centro del círculo hasta el borde del círculo. |
Elemento interactivo
Video: Círculos: Radio, Diámetro y Circunferencia
Práctica: Usar Diámetro, Radio y Pi

