6.6: Área circular
- Page ID
- 107260
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Área de un círculo
Para encontrar el área de un círculo, todo lo que necesitas saber es su radio. Si r es el radio de un círculo, entonces su área es\(A=\pi r^2\).
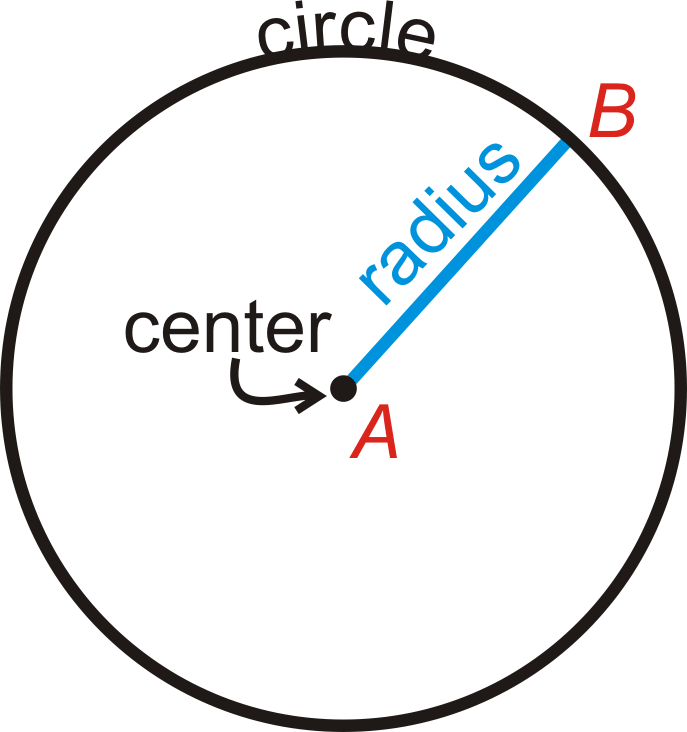
Dejaremos nuestras respuestas en términos de\(\pi\), a menos que se especifique lo contrario.
¿Y si te dieran el radio o diámetro de un círculo? ¿Cómo podrías encontrar la cantidad de espacio que ocupa el círculo?
Ejemplo\(\PageIndex{1}\)
Encuentra el área de un círculo con un diámetro de 12 cm.
Solución
Si\(d=12\text{ cm }\), entonces\(r=6\text{ cm }\). El área es\(A=\pi (6^2)=36\pi \text{ cm }^2\).
Ejemplo\(\PageIndex{2}\)
Si el área de un círculo es\(20\pi \text{ units }\), ¿cuál es el radio?
Solución
Enchufe el área y resuelva para el radio.
\(\begin{aligned} 20\pi &=\pi r^2 \\ 20&=r^2 \\ r&=\sqrt{20}=2\sqrt{5}\text{ units } \end{aligned}\)
Ejemplo\(\PageIndex{3}\)
Un círculo está inscrito en un cuadrado. Cada lado del cuadrado mide 10 cm de largo. ¿Cuál es el área del círculo?
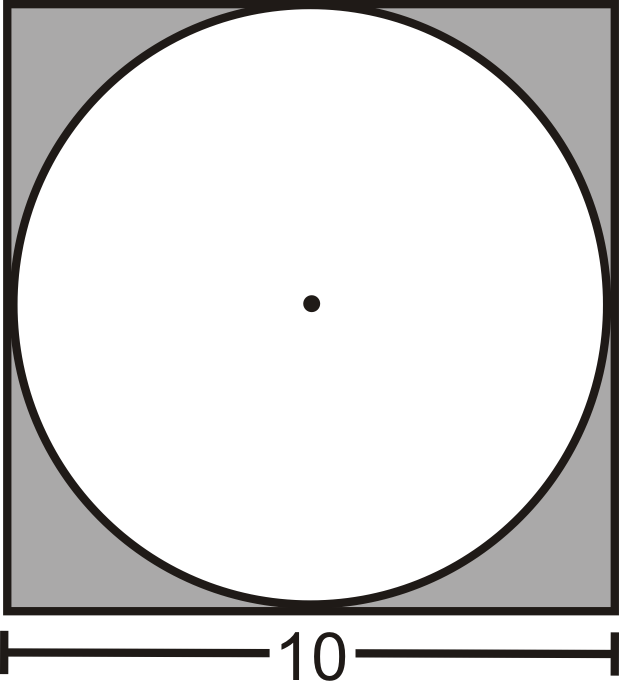
Solución
El diámetro del círculo es el mismo que la longitud de un lado del cuadrado. Por lo tanto, el radio es de 5 cm.
\(A=\pi 5^2=25\pi \text{ cm }^2\)
Ejemplo\(\PageIndex{4}\)
Encuentra el área de la región sombreada del Ejemplo 3.
Solución
El área de la región sombreada sería el área del cuadrado menos el área del círculo.
\(A=102−25\pi =100−25\pi \approx 21.46\text{ cm }^2\)
Ejemplo\(\PageIndex{5}\)
Encuentra el diámetro de un círculo con área\(36\pi \).
Solución
Primero, use la fórmula para el área de un círculo para resolver el radio del círculo.
\(\begin{aligned}A&=\pi r^2 \\ 36\pi &=\pi r^2 \\ 36&=r^2 \\ r&=6\end{aligned}\)
Si el radio es de 6 unidades, entonces el diámetro es de 12 unidades.
Revisar
Rellena la siguiente tabla. Deja todas las respuestas en términos de\(\pi\).
| radio | Área | circunferencia | |
|---|---|---|---|
| 1. | 2 | ||
| 2. | \(16\pi\) | ||
| 3. | \(10\pi\) | ||
| 4. | \(24\pi\) | ||
| 5. | 9 | ||
| 6. | \(90\pi\) | ||
| 7. | \(35\pi\) | ||
| 8. | \(7\pi\) | ||
| 9. | 60 | ||
| 10. | 36 |
Encuentra el área de la región sombreada. Redondee su respuesta a la centésima más cercana.
-
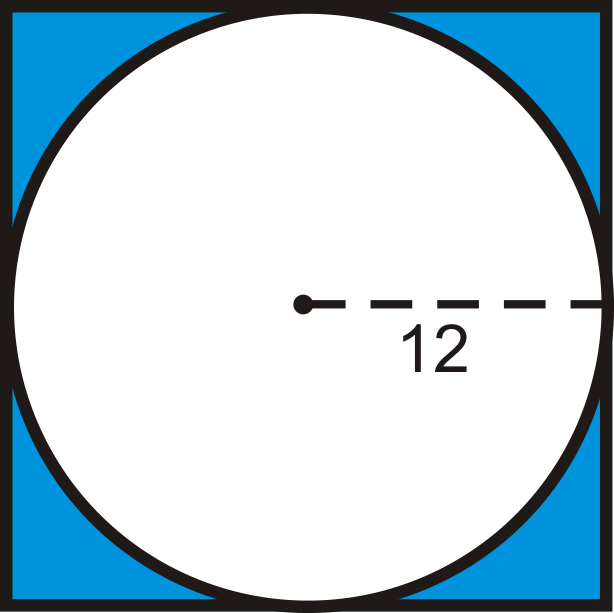
Figura\(\PageIndex{3}\) -
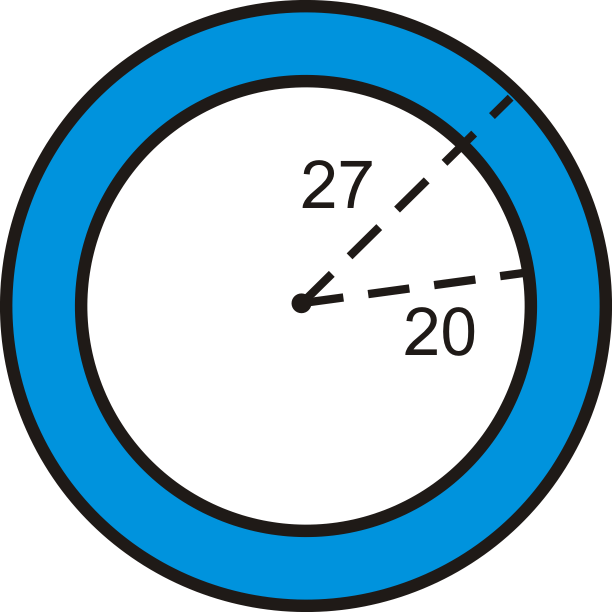
Figura\(\PageIndex{4}\) -
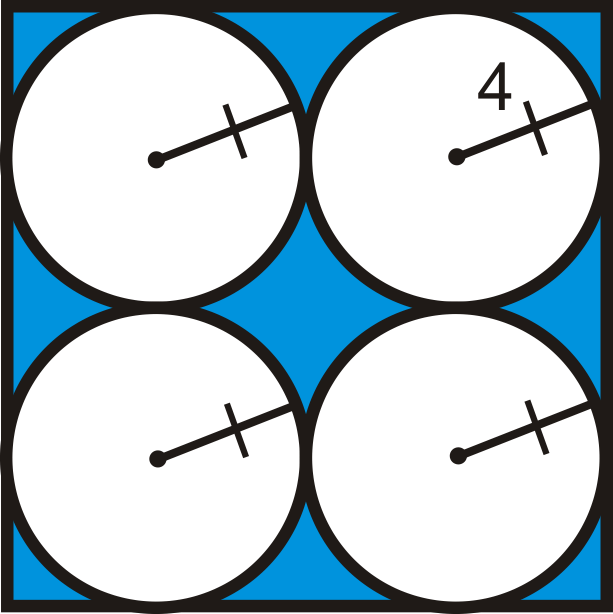
Figura\(\PageIndex{5}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.10.
El vocabulario
| Término | Definición |
|---|---|
| acorde | Un segmento de línea cuyos extremos están en un círculo. |
| círculo | El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el centro. |
| circunferencia | La distancia alrededor de un círculo. |
| diámetro | Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio. |
| pi | (o\(\pi\)) La relación entre la circunferencia de un círculo y su diámetro. |
| radio | La distancia desde el centro hasta el borde exterior de un círculo. |
Recursos adicionales
Elemento interactivo
Video: Determinar el área de un círculo
Actividades: Área de un Círculo Preguntas de Discusión
Ayudas de estudio: Guía de estudio de circunferencia y longitud de arco
Práctica: Área Circular
Mundo real: Asientos en Ringside