6.7: Áreas de figuras combinadas que involucran semicírculos
- Page ID
- 107270
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Calcular áreas de formas irregulares.
Áreas de figuras combinadas que involucran círculos

La mayor parte de la cancha de basquetbol exterior ya estaba repintada de verde. La única parte que quedaba por rehacer era la llave marrón. Los pintores necesitan conocer la superficie total del espacio restante para poder comprar suficiente pintura. Dadas las dimensiones que se muestran a continuación, ¿qué área deben utilizar los trabajadores para calcular sus insumos?
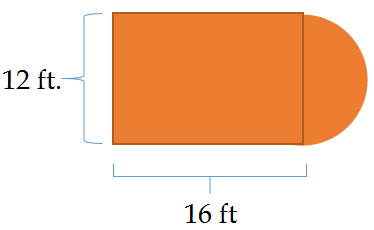
En este concepto, aprenderás a encontrar el área de figuras compuestas que contienen círculos.
Encontrar el área de figuras compuestas
La fórmula para encontrar el área de un rectángulo es\(A=lw\). La fórmula para encontrar el área de un círculo es\(A=\pi r^2\). Para encontrar el área de una forma compuesta, simplemente busque el área de cada forma individual y agréguelas juntas. El orden en que se calculan las áreas no importa, y la propiedad conmutativa establece que no importa en qué orden las agregue.
Veamos un ejemplo.
Encuentra el área de la figura a continuación.
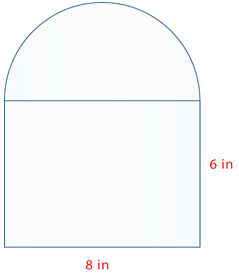
Primero, encuentra el área del rectángulo.
\(\begin{aligned} A&=lw \\ A&=6(8) \\ A&=48\end{aligned}\)
El área del rectángulo es de 48 pulgadas cuadradas.
A continuación, reconozca que se le ha dado un diámetro y necesita dividirlo por 2 para obtener el radio.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(4)^{2} \\ A&=3.14(16) \\ A&=50.24\text{ sq. in. } \end{aligned}\)
El área de un círculo completo es de 50.24 pulgadas cuadradas.
Después, encuentra el área de la mitad del círculo, un semicírculo, dividiendo tu respuesta final por 2.
\(A=25.12\)
El área del semicírculo es de 25.12 pulgadas cuadradas.
Por último, sumar las dos áreas juntas.
\(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=48+25.12 \\ A&=73.12\text{ sq. in. } \end{aligned}\)
La respuesta es que la figura compuesta tiene un área de 73.12 pulgadas cuadradas.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre la cancha de basquetbol al aire libre, que necesita algo de pintura.
Los trabajadores tenían las siguientes dimensiones de corte y necesitan conocer la superficie total para averiguar sus suministros.
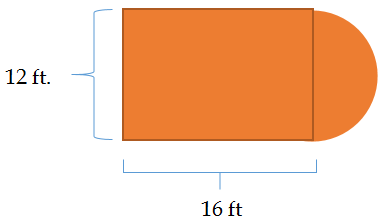
Solución
Primero, encuentra el área del rectángulo.
\(\begin{aligned}A&=lw \\ A&=16(12) \\ A&=192\end{aligned}\)
El área del rectángulo es de 192 pies cuadrados.
A continuación, reconozca que se le ha dado un diámetro y necesita dividirlo por 2 para obtener el radio. El problema establece que el diámetro del círculo es el mismo que el ancho del rectángulo, 3 pies.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(6)^{2} \\ A&=3.14(36) \\ A&=113.04\end{aligned}\)
El área para un círculo completo es de aproximadamente 113 pies cuadrados.
Entonces, recuerda que tienes un semicírculo y divide esta área por 2.
\(A_{sc}=56.5\)
El área del semicírculo es de 56.5 pies cuadrados.
Sumar las dos áreas juntas.
\(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=192+56.5 \\ A&=248.5\text{ sq. ft. }\end{aligned}\)
La respuesta es que la figura compuesta tiene un son\(A=248.5\text{ square feet }\). Los trabajadores necesitarán hacerlo con suficiente pintura para cubrir 248.5 pies cuadrados.
Ejemplo\(\PageIndex{2}\)
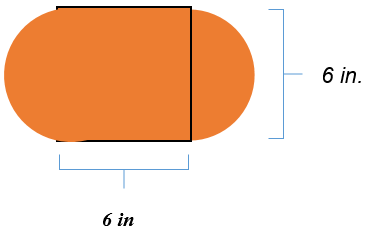
La siguiente figura es de dos semicírculos con un cuadrado en el medio. El cuadrado tiene una longitud lateral de 6 pulgadas.
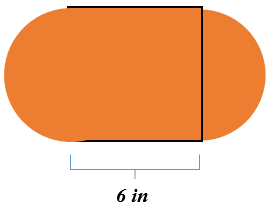
Solución
A continuación, determinar el área de la plaza.
\(\begin{aligned} A&=s^2 \\ A&=6^2 \\ A&=36\end{aligned}\)
El área del cuadrado es de 36 pulgadas cuadradas.
Entonces, reconozca que dado que el cuadrado tiene cuatro lados iguales, el diámetro del círculo también es de 6 pulgadas.
La fórmula para el área de un semicírculo es la fórmula para el área de un círculo dividido por 2.
\(A_{sc}=\dfrac{\pi r^2}{2}\)
Dado que hay dos semicírculos del mismo tamaño, simplemente puede agregarlos juntos para terminar con el área para el círculo completo.
Recuerda que te han dado un diámetro, no un radio, así que divide el diámetro entre 2.
Luego, usa la fórmula para el área de un círculo.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(3)^{2} \\ A&=3.14(9) \\ A&=28.26\end{aligned}\)
El área de los dos semicírculos que forman un círculo completo es de 28.26 pulgadas cuadradas.
Por último, sumar las dos áreas juntas.
\(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=36+28.26 \\ A&=64.26\end{aligned}\)
La respuesta es que la figura compuesta tiene un\(A=64.26\text{ square inches }\)
Ejemplo\(\PageIndex{3}\)
Encuentra el área compuesta de un rectángulo con una longitud de 5 pies y un ancho de 3 pies conectado a un semicírculo con el mismo diámetro que el ancho.
Solución
Primero, encuentra el área del rectángulo.
\(\begin{aligned} A&=lw \\ A&=5(3) \\ A&=15\end{aligned}\)
El área del rectángulo es de 15 pies cuadrados.
A continuación, reconozca que se le ha dado un diámetro y necesita dividirlo por 2 para obtener el radio. El problema establece que el diámetro del círculo es el mismo que el ancho del rectángulo, 3 pies.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(1.5)^{2} \\ A&=3.14(2.25) \\ A&=7.065\end{aligned}\)
El área para un círculo completo es de 7.065 pies cuadrados.
Entonces, recuerda que tienes un semicírculo y divide esta área por 2.
\(A_{sc}=3.53\)
El área del semicírculo es de 3.53 pies cuadrados.
Sumar las dos áreas juntas.
\(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=15+3.53 \\ A&=18.53\text{ sq. ft. }.\end{aligned}\)
La respuesta es que la figura compuesta tiene un son\(A=18.53 \text{ square feet }\).
Ejemplo\(\PageIndex{4}\)
Encuentra el área compuesta de un cuadrado con una longitud lateral de 4 mm y un semicírculo con un diámetro de la misma longitud lateral que el cuadrado.
Solución
Primero, encuentra el área de la plaza.
\(\begin{aligned} A&=s^2 \\ A&=4^2 \\ A&=16 \end{aligned}\)
El área del cuadrado es de 16 milímetros cuadrados.
A continuación, reconozca que se le ha dado un diámetro y necesita dividirlo por 2 para obtener el radio. El problema establece que el diámetro del círculo es el mismo que la longitud lateral del cuadrado, 4 mm.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(2)^{2} \\ A&=3.14(4) \\ A&=12.56\end{aligned}\)
El área para un círculo completo es de 12.56 milímetros cuadrados.
Entonces, recuerda que tienes un semicírculo y divide esta área por 2.
\(A_{sc}=6.28\)
El área del semicírculo es de 6.28 milímetros cuadrados.
Sumar las dos áreas juntas.
\(\begin{aligned} A&=AS+A_{sc} \\ A&=16+6.28 \\ A&=22.28\text{ sq. mm. }\end{aligned}\)
La respuesta es que la figura compuesta tiene un\(A=22.28\text{ sq. mm. }\)
Ejemplo\(\PageIndex{5}\)
Encuentra el área de una figura que está conformada por un cuadrado y un semicírculo. El cuadrado tiene una longitud lateral de 8 pulgadas. El diámetro del círculo es el mismo que el largo lateral del cuadrado.
Solución
Primero, encuentra el área de la plaza.
\(\begin{aligned} A&=s^2 \\ A&=8^2 \\ A&=64\end{aligned} \)
El área del cuadrado es de 64 pulgadas cuadradas.
A continuación, reconozca que se le ha dado un diámetro y necesita dividirlo por 2 para obtener el radio. El problema establece que el diámetro del círculo es el mismo que el largo lateral del cuadrado, 8 pulgadas.
\(\begin{aligned} A&=\pi r^2 \\ A&=3.14(4)^{2} \\ A&=3.14(16) \\ A&=50.24 \end{aligned}\)
El área para un círculo completo es de 50.24 pulgadas cuadradas.
Entonces, recuerda que tienes un semicírculo y divide esta área por 2.
\(A_{sc}=25.12\)
El área del semicírculo es de 25.12 pulgadas cuadradas.
Sumar las dos áreas juntas.
\(\begin{aligned} A&=A_{r}+A_{sc} \\ A&=64+25.12 \\ A&=79.12\text{ square inches } \end{aligned}\)
La respuesta es que la figura compuesta tiene un\(A=79.12\text{ sq. in. }\)
Revisar
Encuentra el área de cada figura combinada.
- Un cuadrado y un semicírculo. El cuadrado tiene una longitud lateral de 11 mm. El diámetro del círculo coincide con el lado del cuadrado.
- Un cuadrado y un semicírculo. El cuadrado tiene una longitud lateral de 8.5 pulgadas. El diámetro del círculo coincide con el lado del cuadrado.
- Un cuadrado y un semicírculo. El cuadrado tiene una longitud lateral de 7.25 pulgadas. El diámetro del círculo coincide con el lado del cuadrado.
- Un cuadrado y un semicírculo. El cuadrado tiene una longitud lateral de 13 pies. El diámetro del círculo coincide con el lado del cuadrado.
- Un cuadrado y un semicírculo. El cuadrado tiene una longitud lateral de 15.5 pies. El diámetro del círculo coincide con el lado del cuadrado.
- Un rectángulo y un semicírculo. El rectángulo tiene una longitud de 8 pies y un ancho de 5 pies. El diámetro del círculo coincide con el ancho.
- Un rectángulo y un semicírculo. El rectángulo tiene una longitud de 8.5 pies y un ancho de 6 pies. El diámetro del círculo coincide con el ancho.
- Un rectángulo y un semicírculo. El rectángulo tiene una longitud de 9 pulgadas y un ancho de 4.5 pulgadas. El diámetro del círculo coincide con la longitud.
- Un rectángulo y un semicírculo. El rectángulo tiene una longitud de 7 pies y un ancho de 4 pies. El diámetro del círculo coincide con la longitud.
- Un rectángulo y un semicírculo. El rectángulo tiene una longitud de 5.5 pies y un ancho de 3.5 pies. El diámetro del círculo coincide con el ancho.
- Un triángulo y un semicírculo. El triángulo tiene una base de 5 pulgadas y una altura de 4 pulgadas. El diámetro del círculo coincide con la base del triángulo.
- Un triángulo y un semicírculo. El triángulo tiene una base de 7 pulgadas y una altura de 6 pulgadas. El diámetro del círculo coincide con la base del triángulo.
- Un triángulo y un semicírculo. El triángulo tiene una base de 5.5 pulgadas y una altura de 4 pulgadas. El diámetro del círculo coincide con la base del triángulo.
Resuelve cada problema.
- Rob está pintando grandes lunares en una hoja para el telón de fondo del musical escolar. Pintó 16 lunares, cada uno con un radio de 3 pies. ¿Cuál es el área total que cubren los lunares?
- La bibliotecaria está teniendo alfombrada la biblioteca de su escuela. La biblioteca es una sala circular con un diámetro de 420 pies. ¿Cuántos pies cuadrados de alfombra necesitará ordenar?
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Área | Área es el espacio dentro del perímetro de una figura bidimensional. |
| Círculo | Un círculo es el conjunto de todos los puntos a una distancia específica de un punto dado en dos dimensiones. |
| Diámetro | El diámetro es la medida de la distancia a través del centro de un círculo. El diámetro es igual al doble de la medida del radio. |
Recursos adicionales
Video: Área y Perímetro
Práctica: Áreas de figuras combinadas que involucran semicírculos
Mundo real: Círculos de tiro

