6.21: Círculos en el plano de coordenadas
- Page ID
- 107249
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Grafica un círculo. Utilizar\((h, k)\) como centro y punto en el círculo. Fórmula:\((x-h)^2 + (y-k)^2 = r^2\) donde\((h, k)\) está el centro y\(r\) es el radio.
Recordemos que un círculo es el conjunto de todos los puntos en un plano que están a la misma distancia del centro. Esta definición se puede utilizar para encontrar una ecuación de un círculo en el plano de coordenadas.
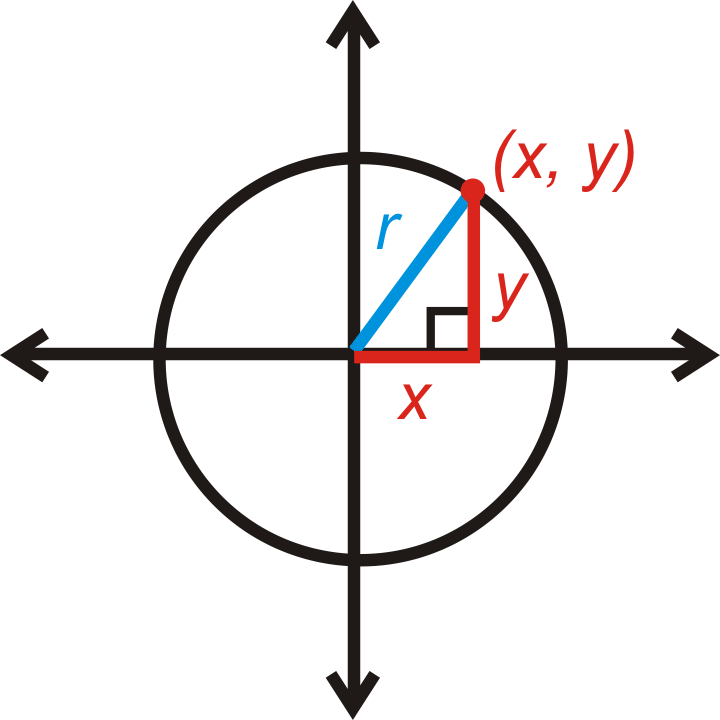
Empecemos con el círculo centrado en\((0, 0)\). Si\((x,y)\) es un punto en el círculo, entonces la distancia desde el centro a este punto sería el radio, r. x es la distancia horizontal e y es la distancia vertical. Esto forma un triángulo rectángulo. Del Teorema de Pitágoras, la ecuación de un círculo centrado en el origen es\(x^2+y^2=r^2\).
El centro no siempre tiene que estar encendido\((0, 0)\). Si no lo es, entonces etiquetamos el centro\((h,k)\). Entonces usaríamos la Fórmula de Distancia para encontrar la longitud del radio.
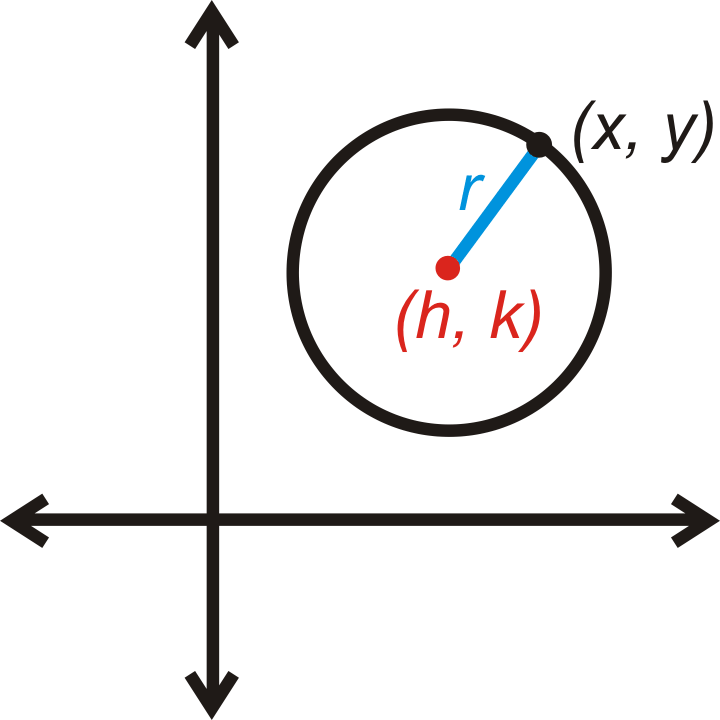
\(r=\sqrt{(x−h)^2+(y−k)^2}\)
Si cuadras ambos lados de esta ecuación, entonces tendrías la ecuación estándar de un círculo. La ecuación estándar de un círculo con centro\((h,k)\) y radio\(r\) es\(r^2=(x−h)^2+(y−k)^2\).
¿Y si te dieran la longitud del radio de un círculo y las coordenadas de su centro? ¿Cómo se podría escribir la ecuación del círculo en el plano de coordenadas?
Ejemplo\(\PageIndex{1}\)
Encuentra el centro y el radio del siguiente círculo.
\((x+2)^2+(y−5)^2=49\)
Solución
Reescribe la ecuación como\((x−(−2))^2+(y−5)^2=7^2\). El centro es\((-2, 5)\) y\(r=7\).
Tenga en cuenta que, debido a los signos menos en la fórmula, las coordenadas del centro tienen los signos opuestos de lo que inicialmente pueden parecer ser.
Ejemplo\(\PageIndex{2}\)
Encuentra el centro y el radio del siguiente círculo.
Encuentra la ecuación del círculo con el centro\((4, -1)\) y que pasa a través\((-1, 2)\).
Solución
Primero enchufa el centro a la ecuación estándar.
\(\begin{aligned} (x−4)^2+(y−(−1))^2&=r^2 \\ (x−4)^2+(y+1)^2&=r^2\end{aligned}\)
Ahora, conecte (-1, 2) para\(x\) y\(y\) y resuelva para\(r\).
\(\begin{aligned} (−1−4)^2+(2+1)^2=r^2 \\ (−5)^2+(3)^2&=r^2 \\ 25+9&=r^2 \\ 34&=r^2\end{aligned}\)
Sustituyendo\(34\) por\(r^2\), la ecuación es\((x−4)^2+(y+1)^2=34\).
Ejemplo\(\PageIndex{3}\)
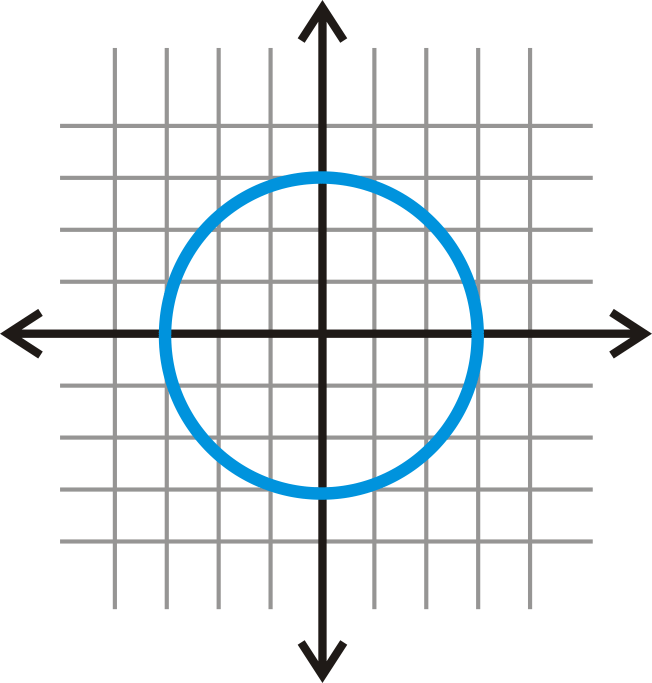
Gráfica\(x^2+y^2=9\).
Solución
El centro es\((0, 0)\). Su radio es la raíz cuadrada de 9, o 3. Traza el centro, traza los puntos que son 3 unidades a la derecha, izquierda, arriba y abajo desde el centro y luego conecta estos cuatro puntos para formar un círculo.
Ejemplo\(\PageIndex{4\)
Encuentra la ecuación del círculo a continuación.
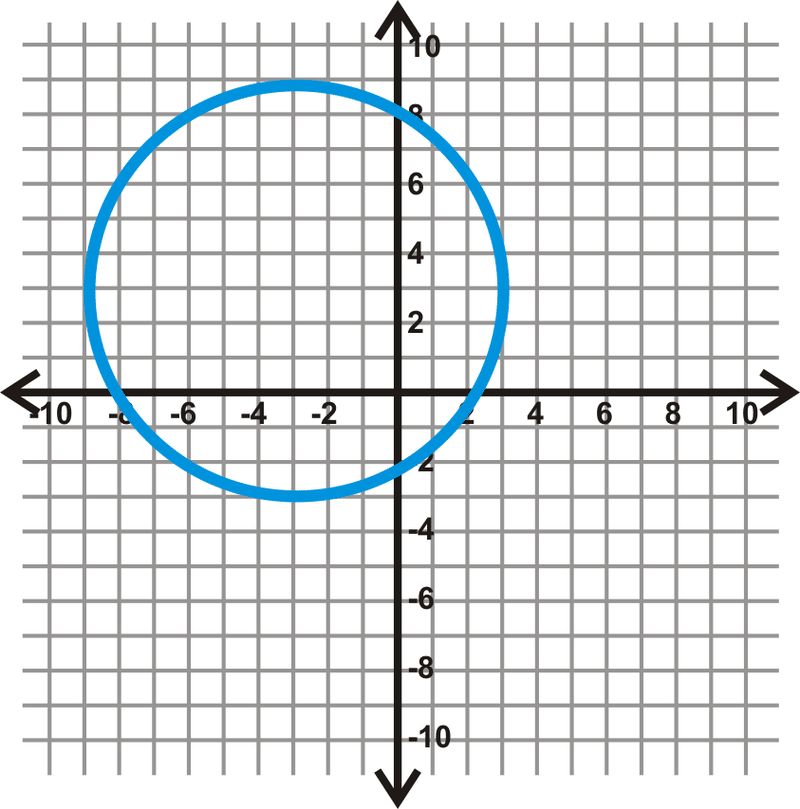
Solución
Primero localice el centro. Dibuje en los diámetros horizontal y vertical para ver dónde se cruzan.
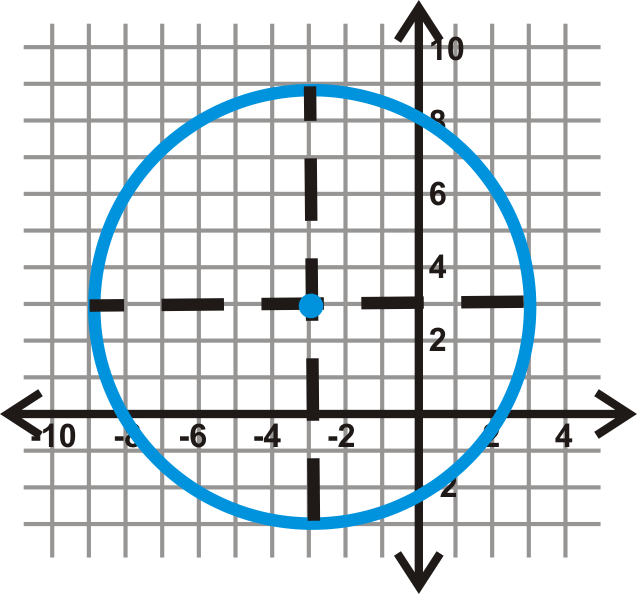
A partir de esto, vemos que el centro es\((-3, 3)\). Si contamos las unidades desde el centro hasta el círculo en cualquiera de estos diámetros, nos encontramos\(r=6\). Conectando esto a la ecuación de un círculo, obtenemos:\((x−(−3))^2+(y−3)^2=6^2\) o\((x+3)^2+(y−3)^2=36\).
Ejemplo\(\PageIndex{5}\)
Determinar si los siguientes puntos están encendidos\((x+1)^2+(y−5)^2=50\).
Solución
Enchufe los puntos para x e y adentro\((x+1)^2+(y−5)^2=50\).
- \((8, -3)\)
\(\begin{aligned} (8+1)^2+(−3−5)^2&=50 \\ 9^2+(−8)^2&=50 \\ 81+64 &\neq 50\end{aligned}\)
\((8, -3)\)no está en el círculo
- \((-2, -2)\)
\(\begin{aligned} (−2+1)^2+(−2−5)^2&=50 \\ (−1)^2+(−7)^2&=50 \\ 1+49&=50\end{aligned}\)
\( (-2, -2)\)está en el círculo
Revisar
Encuentra el centro y el radio de cada círculo. Después, grafica cada círculo.
- \((x+5)^2+(y−3)^2=16\)
- \ (x^2+ (y+8) ^2=4
- \ ((x−7) ^2+ (y−10) ^2=20
- \ ((x+2) ^2+y^2=8
Encuentra la ecuación de los círculos a continuación.
-
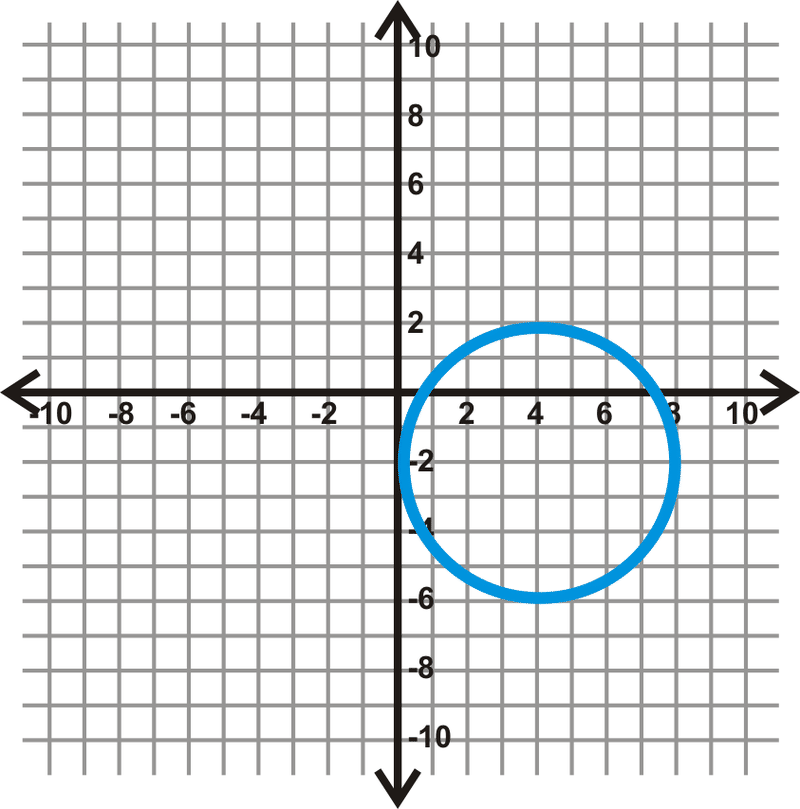
Figura\(\PageIndex{6}\) -
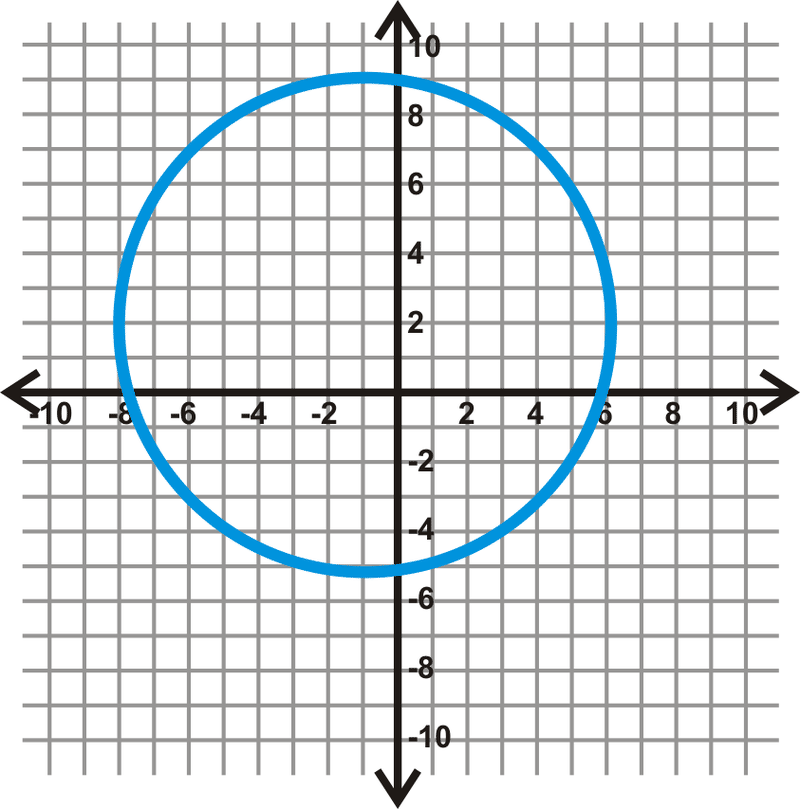
Figura\(\PageIndex{7}\) -
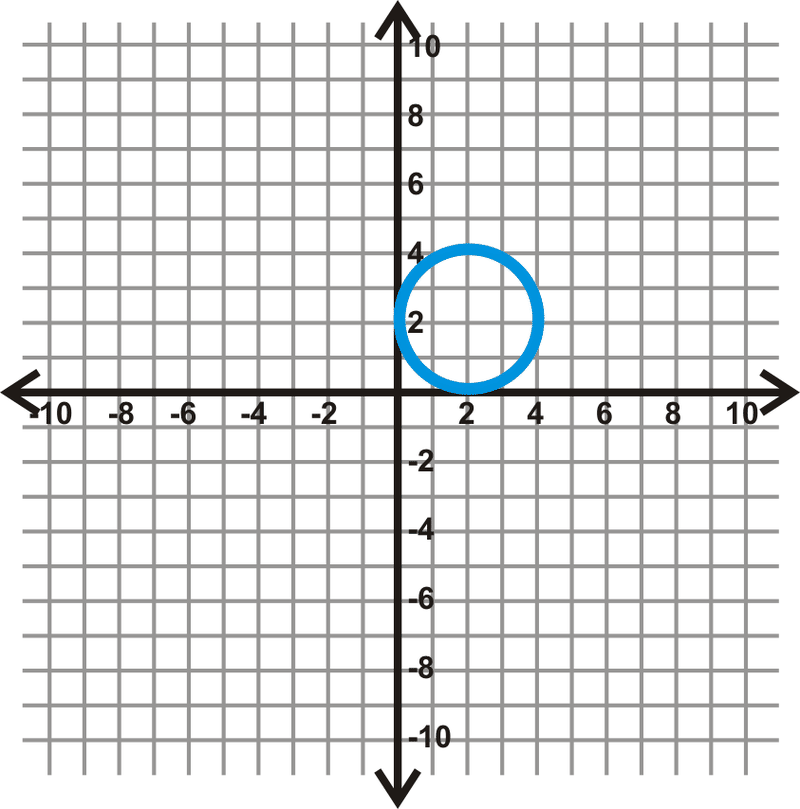
Figura\(\PageIndex{8}\) -
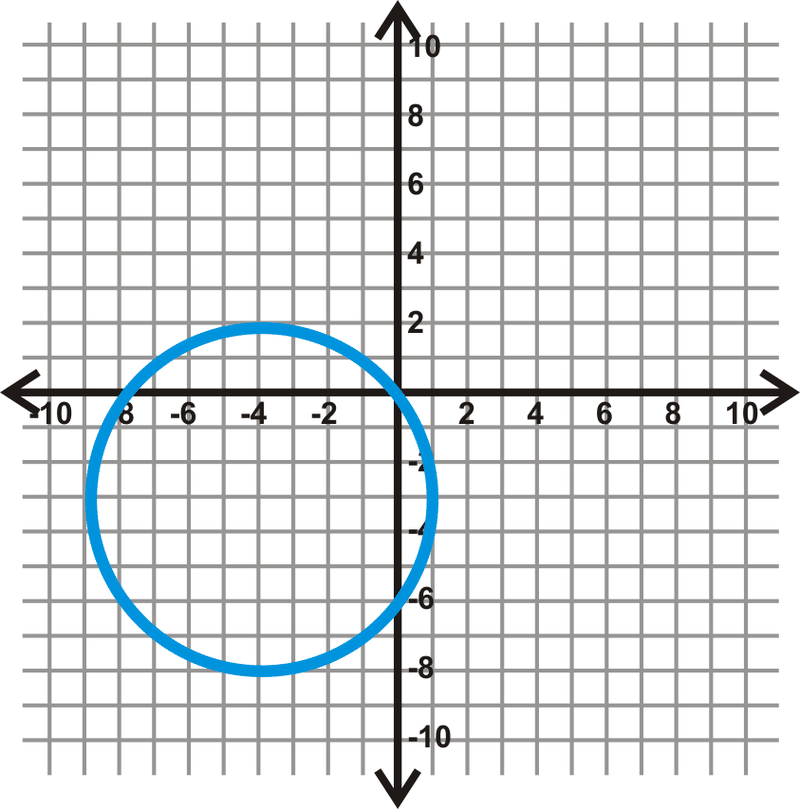
Figura\(\PageIndex{9}\) - ¿Está encendido (-7, 3)\((x+1)^2+(y−6)^2=45\)?
- ¿Está encendido (9, -1)\((x−2)^2+(y−2)^2=60\)?
- ¿Está encendido (-4, -3)\((x+3)^2+(y−3)^2=37\)?
- ¿Está encendido (5, -3)\((x+1)^2+(y−6)^2=45\)?
Encuentra la ecuación del círculo con el centro dado y el punto en el círculo.
- centro: (2, 3), punto: (-4, -1)
- centro: (10, 0), punto: (5, 2)
- centro: (-3, 8), punto: (7, -2)
- centro: (6, -6), punto: (-9, 4)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 9.12.
El vocabulario
| Término | Definición |
|---|---|
| círculo | El conjunto de todos los puntos que están a la misma distancia de un punto específico, llamado el centro. |
| radio | La distancia desde el centro hasta el borde exterior de un círculo. |
| Fórmula de distancia | La distancia entre dos puntos\((x_1, y_1)\) y se\((x_2, y_2)\) puede definir como\(d=\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\). |
| Origen | El origen es el punto de intersección de los ejes x e y en el plano cartesiano. Las coordenadas del origen son (0, 0). |
Recursos adicionales
Elemento Interactivo
Video: Graficando Círculos Principios - Básico
Actividades: Círculos en el Plano Coordinado Preguntas de Discusión
Ayudas de estudio: Propiedades de una guía de estudio circular
Práctica: Círculos en el plano de coordenadas
Mundo real: Geometría GPS