9.1: Poliedros
- Page ID
- 107221
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Figuras 3-D formadas por polígonos que encierran regiones en el espacio.
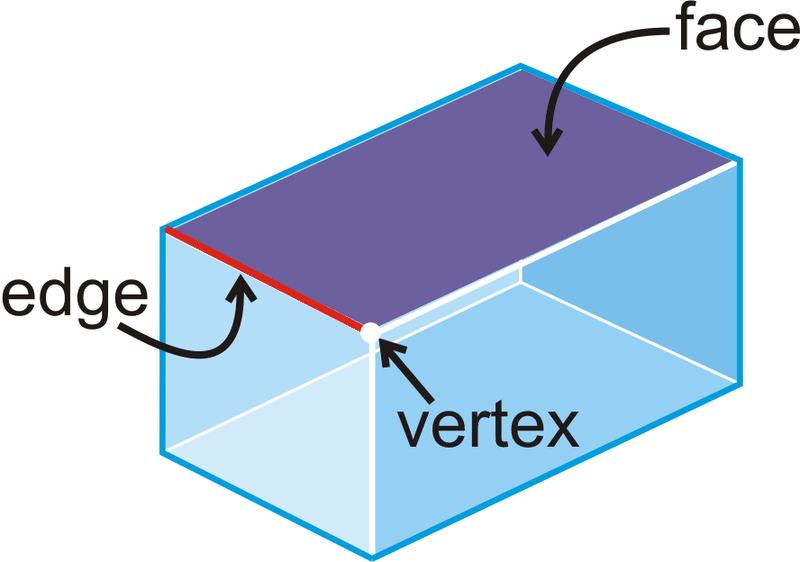
Un poliedro es una figura tridimensional que está formada por polígonos que encierran una región en el espacio. Cada polígono en un poliedro es una cara . El segmento de línea donde se cruzan dos caras es una arista . El punto de intersección de dos aristas es un vértice .
Los ejemplos de poliedros incluyen un cubo, prisma o pirámide. Los conos, las esferas y los cilindros no son poliedros porque tienen superficies que no son polígonos. Los siguientes son más ejemplos de poliedros:
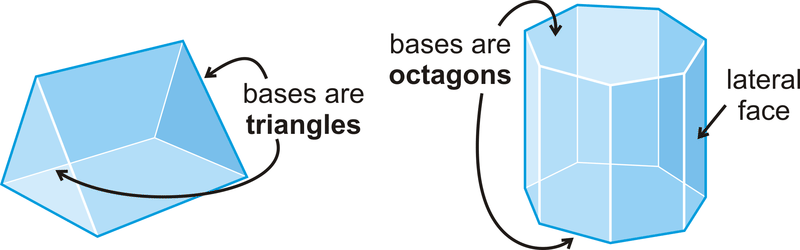
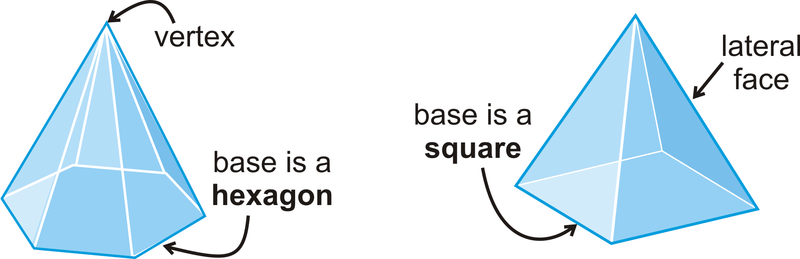
El número de caras (\(F\)), vértices (\(V\)) y aristas (\(E\)) están relacionados de la misma manera para cualquier poliedro. Su relación fue descubierta por el matemático suizo Leonhard Euler, y se llama Teorema de Euler.
Teorema de Euler:\(F+V=E+2\).
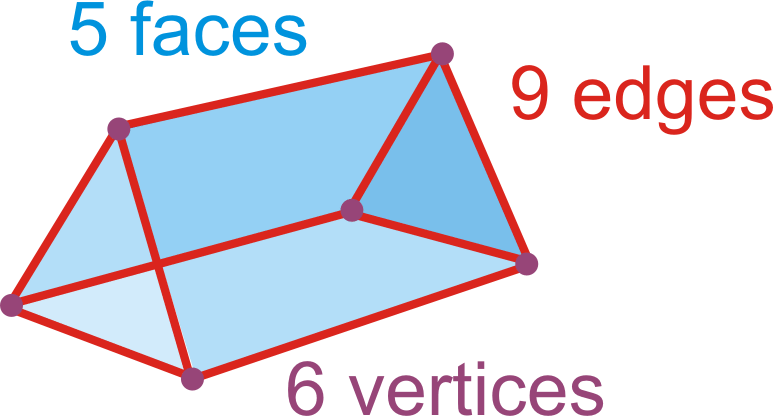
\(Faces+Vertices=Edges+2\)
\(5+6=9+2\)
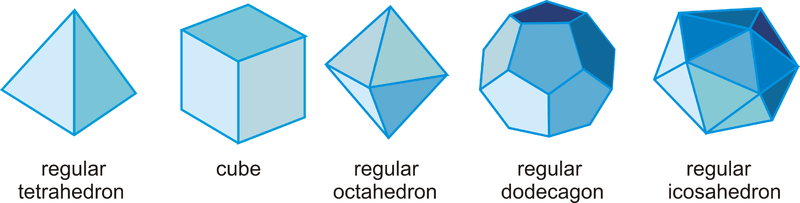
Un poliedro regular es un poliedro donde todas las caras son polígonos regulares congruentes. Sólo hay cinco poliedros regulares, llamados los sólidos platónicos.
- Tetraedro Regular: Un poliedro de 4 caras y todas las caras son triángulos equiláteros.
- Cubo: Un poliedro de 6 caras y todas las caras son cuadradas.
- Octaedro Regular: Un poliedro de 8 caras y todas las caras son triángulos equiláteros.
- Dodecaedro regular: Un poliedro de 12 caras y todas las caras son pentágonos regulares.
- Icosaedro regular: Un poliedro de 20 caras y todas las caras son triángulos equiláteros.
¿Y si te dieran una figura tridimensional sólida, como una caja de helado? ¿Cómo podría determinar cómo se relacionan las caras, los vértices y los bordes de esa figura?
Ejemplo\(\PageIndex{1}\)
-
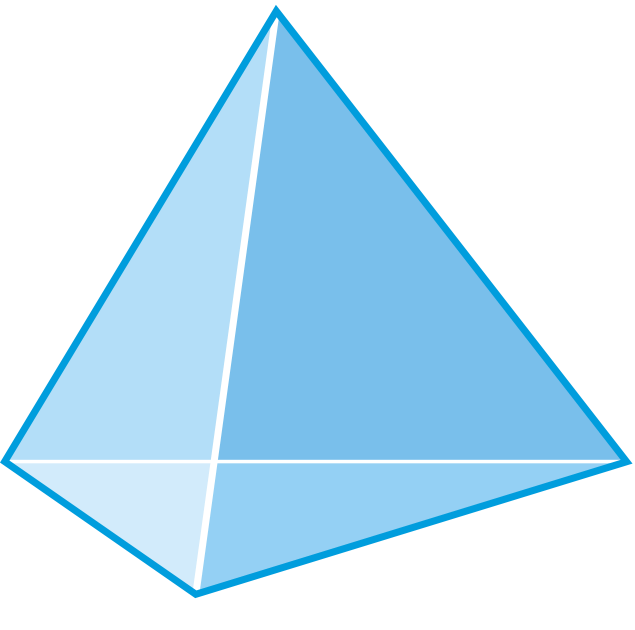
Figura\(\PageIndex{6}\) -
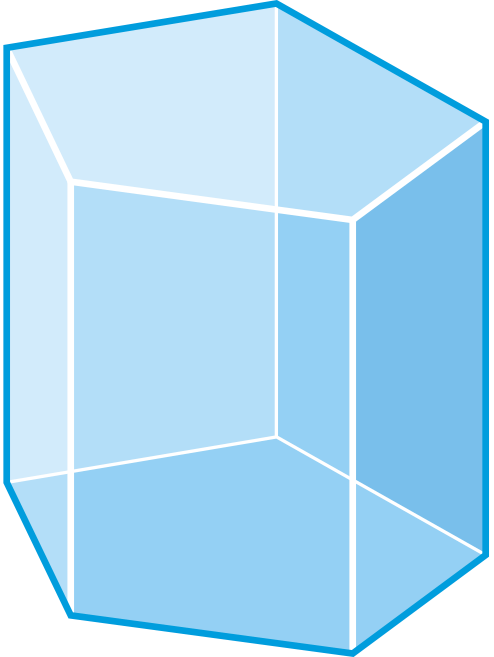
Figura\(\PageIndex{7}\) -
Figura\(\PageIndex{8}\)
Solución
La base es un triángulo y todos los lados son triángulos, por lo que esta es una pirámide triangular, que también se conoce como tetraedro. Hay 4 caras, 6 aristas y 4 vértices.
Ejemplo\(\PageIndex{2}\)
En un poliedro de seis caras, hay 10 bordes. ¿Cuántos vértices tiene el poliedro?
Solución
Resolver para\(V\) en el Teorema de Euler.
\(\begin{aligned} F+V&=E+2 \\ 6+V&=10+2 \\ V&=6\end{aligned} \)
Por lo tanto, hay 6 vértices.
Ejemplo\(\PageIndex{3}\)
Markus cuenta los bordes, caras y vértices de un poliedro. Se le ocurre 10 vértices, 5 caras y 12 aristas. ¿Cometió un error?
Solución
Enchufa los tres números en el Teorema de Euler.
\(\begin{aligned} F+V&=E+2 \\ 5+10&=12+2 \\ 15 &\neq 14 \end{aligned}\)
Debido a que las dos partes no son iguales, Markus cometió un error.
Ejemplo\(\PageIndex{4}\)
Encuentra el número de caras, vértices y aristas en un prisma octogonal.
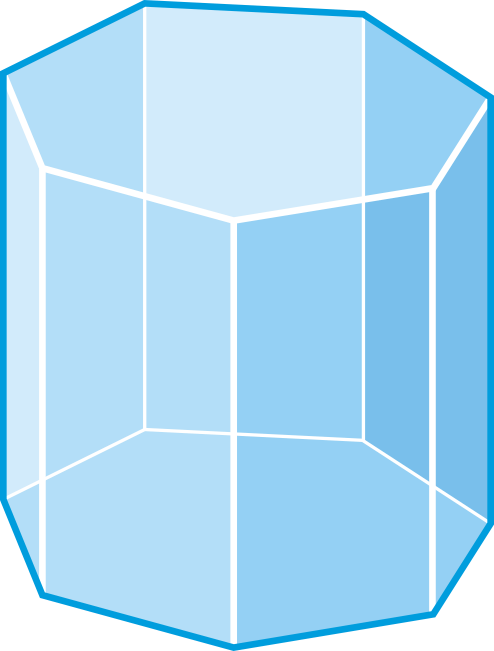
Solución
Hay 10 caras y 16 vértices. Usa el Teorema de Euler, para resolver para\(E\).
\(\begin{aligned} F+V&=E+2 \\ 10+16&=E+2 \\ 24&=E \end{aligned}\)
Por lo tanto, hay 24 bordes.
Ejemplo\(\PageIndex{5}\)
Un icosaedro truncado es un poliedro con 12 caras pentagonales regulares, 20 caras hexagonales regulares y 90 bordes. Este icosaedro se parece mucho a un balón de fútbol. ¿Cuántos vértices tiene? Explica tu razonamiento.
Solución
Podemos usar el Teorema de Euler para resolver el número de vértices.
\(\begin{aligned} F+V&=E+2 \\ 32+V&=90+2 \\ V&=60\end{aligned}\)
Por lo tanto, tiene 60 vértices.
Revisar
Completa la tabla usando el Teorema de Euler.
| Nombre | Caras | Bordes | Vértices | |
|---|---|---|---|---|
| 1. | Prisma Rectangular | 6 | 12 | |
| 2. | Pirámide octogonal | 16 | 9 | |
| 3. | Icosaedro regular | 20 | 12 | |
| 4. | Cube | 12 | 8 | |
| 5. | Pirámide Triangular | 4 | 4 | |
| 6. | Octaedro | 8 | 12 | |
| 7. | Prisma Heptagonal | 21 | 14 | |
| 8. | Prisma Triangular | 5 | 9 |
Determinar si las siguientes cifras son poliedros. Si es así, asigne un nombre a la figura y busca el número de caras, aristas y vértices.
-
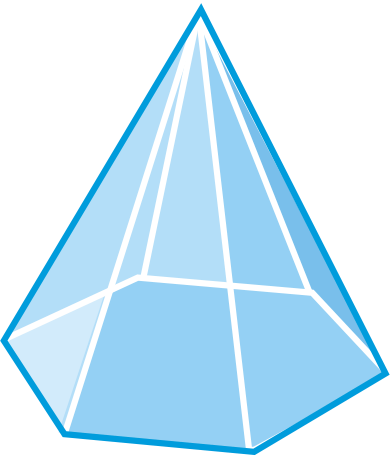
Figura\(\PageIndex{11}\) -
Figura\(\PageIndex{12}\) -
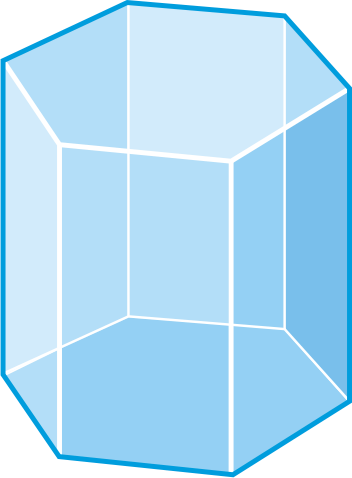
Figura\(\PageIndex{13}\) -
Figura\(\PageIndex{14}\) -
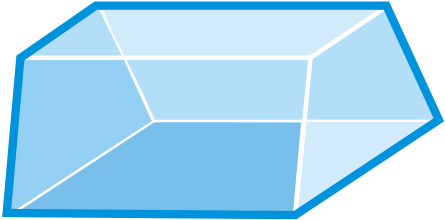
Figura\(\PageIndex{15}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.1.
Recursos adicionales
Video: Principios de Poliedros - Básicos
Actividades: Preguntas de discusión sobre poliedros
Ayudas de estudio: Guía de estudio de poliedros
Práctica: Poliedros
Mundo Real: ¡Roly Poly Poliedro!