9.22: Superficie y Volumen de Conos
- Page ID
- 107228
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El área de superficie es igual al área del círculo más el área del exterior del cono
Conos
Un cono es un sólido con una base circular y lados que se inclinan hacia un vértice. Un cono se genera a partir de la rotación de un triángulo rectángulo, alrededor de una pata. Un cono tiene una altura inclinada.
Superficie
El área superficial es una medida bidimensional que es el área total de todas las superficies que enlazan un sólido. La unidad básica de área es la unidad cuadrada. Para la superficie de un cono necesitamos la suma del área de la base y el área de los lados.
Área de superficie de un cono derecho:\(SA= \pi r^{2}+ \pi rl\).
Área de la base:\(\pi r^{2}\)
Área de los lados:\(\pi rl\)
Volumen
Para encontrar el volumen de cualquier sólido debes averiguar cuánto espacio ocupa. La unidad básica de volumen es la unidad cúbica.
Volumen de un Cono:\(V=\dfrac{1}{3} \pi r^{2} h\).
¿Y si te dieran una figura sólida tridimensional con una base circular y lados que se ahusaban hacia un vértice? ¿Cómo podrías determinar cuánto espacio bidimensional y tridimensional ocupa esa figura?
Ejemplo\(\PageIndex{1}\)
El área de superficie de un cono es\(36 \pi\) y el radio es de 4 unidades. ¿Cuál es la altura inclinada?
Solución
Conecte lo que sabe en la fórmula para el área de superficie de un cono y resuelva para\(l\).
\(\begin{aligned} 36 \pi&= \pi 4^{2}+ \pi 4l \\ 36&=16+4l \qquad \text{ When each term has a } \pi \text{, they cancel out.} \\ 20&=4l \\ 5&=l\end{aligned}\)
Ejemplo\(\PageIndex{2}\)
El volumen de un cono es\(484 \pi \text{ cm}^{3}\) y la altura es de 12 cm. ¿Cuál es el radio?
Solución
Enchufa lo que sabes a la fórmula de volumen.
\(\begin{aligned} 484 \pi&=\dfrac{1}{3} \pi r^{2}(12) \\ 121&=r^{2} \\ 11 \text{ cm}&=r\end{aligned}\)
Ejemplo\(\PageIndex{3}\)
¿Cuál es la superficie del cono?
Solución
Primero, necesitamos encontrar la altura inclinada. Usa el Teorema de Pitágoras.
\(\begin{aligned} l^{2}&=9^{2}+21^{2} \\ &=81+441 \\ l&=\sqrt{522}\cong 22.85\end{aligned]\)
La superficie total, entonces, es\(SA= \pi 9^{2}+ \pi(9)(22.85)\cong 900.54 \text{ units}^{2}\).
Ejemplo\(\PageIndex{4}\)
Encuentra el volumen del cono.
Solución
Primero, necesitamos la altura. Usa el Teorema de Pitágoras.
\(\begin{aligned} 5^{2}+h^{2}&=15^{2} \\ h&=\sqrt{200}=10\sqrt{2} \\ V&=13(5^{2})(10\sqrt{2}) \pi \cong 370.24 \text{ units}^{3}\end{aligned}\)
Ejemplo\(\PageIndex{5}\)
Encuentra el volumen del cono.
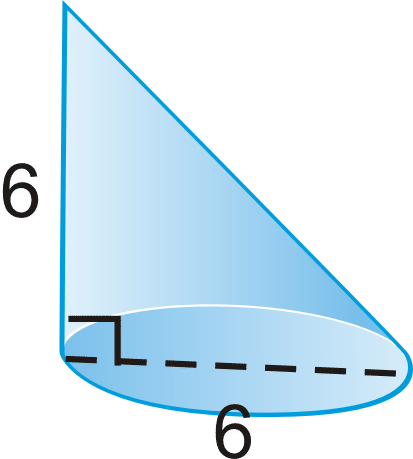
Solución
Podemos usar la misma fórmula de volumen. Encuentra el radio.
\(V=\dfrac{1}{3} \pi(3^{2})(6)=18 \pi \cong 56.55 \text{ units}^{3}\)
Revisar
Usa el cono para rellenar los espacios en blanco.
- v es el ___________.
- La altura del cono es ______.
- x es un __________ y es el ___________ del cono.
- w es el _____________ ____________.
Esbozar el siguiente sólido y responder a la pregunta. Tu dibujo debe ser a escala, pero no uno a uno. Deja tu respuesta en forma radical más simple.
- Dibuja un cono derecho con un radio de 5 cm y una altura de 15 cm. ¿Cuál es la altura inclinada?
Encuentra la altura inclinada,\(l\), de una cara lateral en el cono. Redondea tu respuesta a la centésima más cercana.
-
Figura\(\PageIndex{9}\)
Encuentra el área de superficie y el volumen de los conos correctos. Redondea tus respuestas a 2 decimales.
-
Figura\(\PageIndex{10}\) -
Figura\(\PageIndex{11}\) - Si la superficie lateral de un cono es\(30 \pi \text{ cm}^{2}\) y el radio es de 5 cm, ¿cuál es la altura inclinada?
- Si la superficie de un cono es\(105 \pi \text{ cm}^{2}\) y la altura inclinada es de 8 cm, ¿cuál es el radio?
- Si el volumen de un cono es\( 30 \pi \text{ cm}^{3}\) y el radio es de 5 cm, ¿cuál es la altura?
- Si el volumen de un cono es\(105 \pi \text{ cm}^{3}\) y la altura es de 35 cm, ¿cuál es el radio?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.6.
El vocabulario
| Término | Definición |
|---|---|
| cono | es un sólido con una base circular y lados que se inclinan hacia un vértice. Un cono tiene una altura inclinada. |
| Altura Inclinada | La altura inclinada es la altura de una cara lateral de una pirámide. |
Recursos adicionales
Elemento Interactivo
Video: Área de superficie del cono - Descripción general
Actividades: Conos Preguntas de Discusión
Ayudas de estudio: Guía de estudio de pirámides y conos
Práctica: Superficie y Volumen de Conos