9.25: Superficie y Volumen de Esferas
- Page ID
- 107222
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Derive y usa la fórmula: volumen es igual a\(\dfrac{4}{3}\) veces pi por el radio en cubos.
Esferas
Considera una figura sólida que consiste en el conjunto de todos los puntos en el espacio tridimensional que son equidistantes de un solo punto. ¿Cómo podrías determinar cuánto espacio bidimensional y tridimensional ocupa esa figura?
Una esfera es el conjunto de todos los puntos en el espacio tridimensional que son equidistantes de un solo punto. El radio de una esfera tiene un punto final en la superficie de la esfera y el otro punto final en el centro de esa esfera. El diámetro de una esfera debe contener el centro.
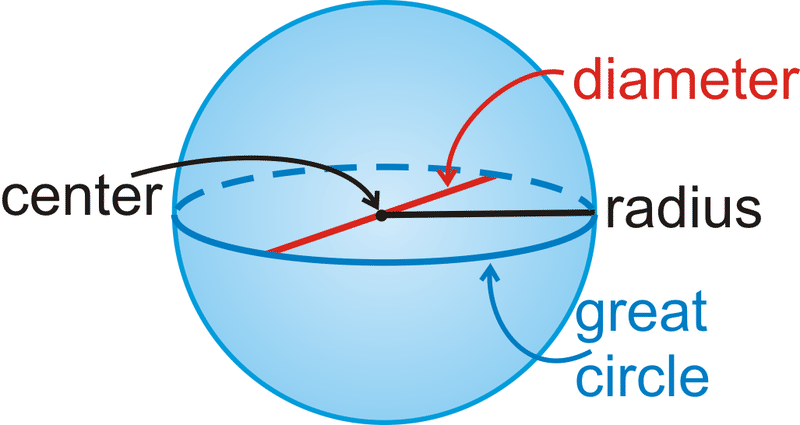
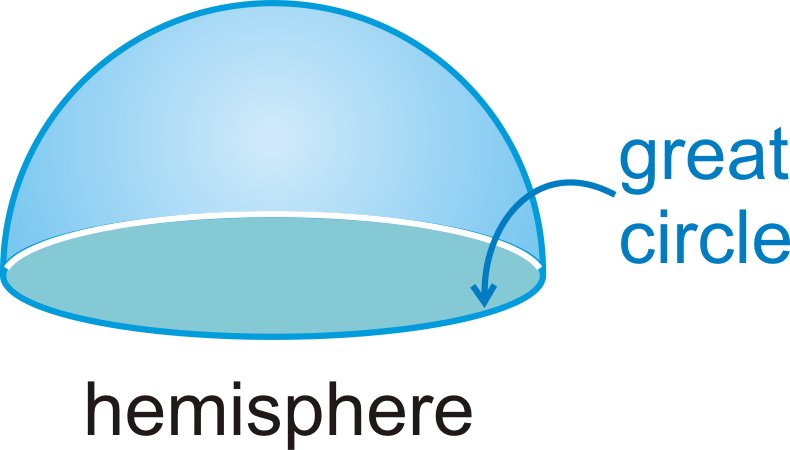
Un gran círculo es la sección transversal circular más grande en una esfera. La circunferencia de una esfera es la circunferencia de un gran círculo. Cada gran círculo divide una esfera en dos hemisferios congruentes .
Superficie
El área superficial es una medida bidimensional que es el área total de todas las superficies que enlazan un sólido. La unidad básica de área es la unidad cuadrada.
Superficie de una esfera:\(SA=4\pi r^{2}\)
Volumen
Para encontrar el volumen de cualquier sólido debes averiguar cuánto espacio ocupa. La unidad básica de volumen es la unidad cúbica.
Volumen de una Esfera:\(V=\dfrac{4}{3}\pi r^{3}\)

Ejemplo\(\PageIndex{1}\)
Encuentra el área de superficie de la figura de abajo, un hemisferio con una base circular.
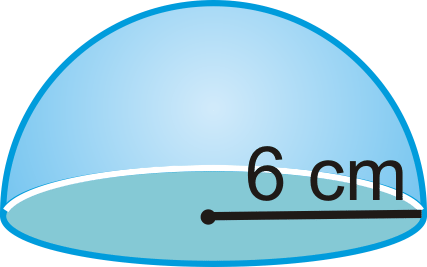
Solución
Utilice la fórmula para el área de superficie:
\(\begin{aligned} SA&=\pi r^{2} +124\pi r^{2} \\ &=\pi (6^{2})+2\pi (6^{2}) \\&=36\pi +72\pi =108\pi \text{ cm}^{2}\end{aligned}\)
Ejemplo\(\PageIndex{2}\)
Una esfera tiene un volumen de 14,137.167 pies3. ¿Cuál es el radio?
Solución
Usa la fórmula para volumen, enchufa el volumen dado y resuelve para el radio, r:
\(\begin{aligned} V&=\dfrac{4}{3}\pi r^{3} \\ 14,137.167&=\dfrac{4}{3}\pi r^{3} \\ \dfrac{3}{4\pi} \cdot 14,137.167&=r^{3} \\ 3375&\approx r^{3}\end{aligned}\)
En este punto, necesitarás tomar la raíz cúbica de 3375. Tu calculadora podría tener un botón que se parece a\ sqrt [3] {}, o puedes usar\(3375^{\dfrac{1}{3}}\).
\(\sqrt[3]{3375}=15\approx r\)
Ejemplo\(\PageIndex{3}\)
La circunferencia de una esfera es de 26\ pi pies. ¿Cuál es el radio de la esfera?
Solución
La circunferencia se refiere a la circunferencia de un gran círculo.
Uso\(C=2\pi r\):
\(\begin{aligned} 2\pi r&=26\pi \\ r&=13\text{ ft}\end{aligned}\)
Ejemplo\(\PageIndex{4}\)
Encuentra el área de superficie de una esfera con un radio de 14 pies.
Solución
Utilice la fórmula para el área de superficie:
\(SA=4\pi (14)^{2}\)
\(=784\pi \text{ ft}^{2}\)\)
Ejemplo\(\PageIndex{5}\)
Encuentra el volumen de una esfera con un radio de 6 m.
Solución
Utilice la fórmula para el volumen:
\(\begin{aligned} V&=\dfrac{4}{3}\pi 63 \\ &=\dfrac{4}{3}\pi (216) \\ &=288\pi \text{ m}^{3}\end{aligned}\)
Revisar
- ¿Hay alguna sección transversal de una esfera que no sea un círculo? Explica tu respuesta.
- Enumere todas las partes de una esfera que son iguales a un círculo.
- Enumere cualquier parte de una esfera que no tenga un círculo.
Para 4 - 11, encuentre el área superficial y el volumen de una esfera con la dimensión dada. Deja tu respuesta en términos de\(\pi\).
- un radio de 8 pulg.
- un diámetro de 18 cm.
- un radio de 20 pies
- un diámetro de 4 m.
- un radio de 15 pies
- un diámetro de 32 pulg.
- una circunferencia de\(26\pi \text{ cm}\).
- una circunferencia de\(50\pi\text{ yds}\).
- La superficie de una esfera es\(121\pi \text{ in}^{2}\). ¿Cuál es el radio?
- El volumen de una esfera es\(47916\pi \text{ m}^{3}\). ¿Cuál es el radio?
- La superficie de una esfera es\(4\pi \text{ ft}^{2}\). ¿Cuál es el volumen?
- El volumen de una esfera es\(36\pi \text{ mi}^{3}\). ¿Cuál es la superficie?
- Encuentra el radio de la esfera que tiene un volumen de\(335 \text{ cm}^{3}\). Redondea tu respuesta a la centésima más cercana.
- Encuentra el radio de la esfera que tiene un área de superficie\(225\pi \text{ ft}^{2}\).
Encuentra el área de superficie y volumen de la siguiente forma. Deja tus respuestas en términos de\ pi.
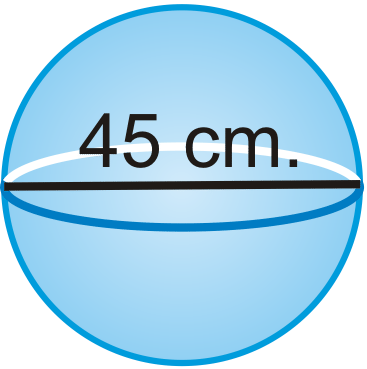
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 11.7.
El vocabulario
| Término | Definición |
|---|---|
| diámetro | Un acorde que pasa por el centro del círculo. La longitud de un diámetro es dos veces la longitud de un radio. |
| Esfera | Una esfera es un sólido redondo y tridimensional. Todos los puntos de la superficie de una esfera son equidistantes del centro de la esfera. |
| Radio | El radio de un círculo es la distancia desde el centro del círculo hasta el borde del círculo. |
| Volumen | Volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |
| Principio de Cavalieri | Afirma que si dos sólidos tienen la misma altura y la misma área de sección transversal en cada nivel, entonces tendrán el mismo volumen. |
Recursos adicionales
Elemento interactivo
Video: Principios de Esferas - Básicos
Actividades: Preguntas de Discusión de Esferas
Ayudas de estudio: Guía de estudio de esferas
Práctica: Superficie y Volumen de Esferas
Mundo Real: ¡Dónde Vivimos!

