9.2: Caras, aristas y vértices de sólidos
- Page ID
- 107321
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Apoyándose en lo que hace un sólido, identifique y cuente los elementos, incluyendo caras, aristas y vértices de prismas, cilindros, conos

Gayle eligió las aves migratorias como tema de su proyecto de clase de biología. Ha elegido 12 imágenes de diferentes aves para exhibir como parte de su ensayo fotográfico. Ella planea comprar marcos de fotos en forma de cubo que le permitan colocar una foto a cada lado del cubo. ¿Cuántos de los marcos de fotos necesita Gayle para enmarcar las 12 fotos?
En este concepto, aprenderás a identificar las caras, aristas y vértices de figuras sólidas.
Identificación de caras, aristas y vértices de figuras sólidas
Una figura sólida se puede definir por el número y combinación de ciertas partes. Estas partes son:
- Caras
- Bordes
- Vértices
Estas tres partes son relevantes para cualquier sólido que tenga superficies planas, lugares donde las superficies planas se cruzan y lugares donde los planos se cruzan.
Definamos cada parte.
Una cara es cualquier superficie plana. La superficie plana que hace el frente de este cubo se llama cara. Muchas figuras sólidas tienen más de una cara.
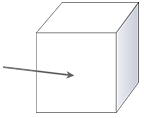
Una arista es el segmento de línea donde dos caras se encuentran. Se puede ver mirando este cubo que las caras se cruzan en una línea. Muchas figuras sólidas tienen más de un borde.
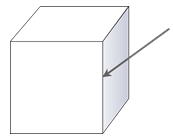
Un vértice es un punto donde varios planos se encuentran en un punto. La flecha aquí está apuntando a un vértice de este cubo. Muchos sólidos tienen más de un vértice, o muchos vértices.
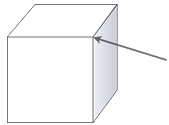
Veamos la identificación del número de caras, aristas y vértices de una figura sólida.
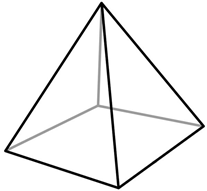
Esta es una pirámide cuadrada.
Las caras son los lados triangulares y el fondo cuadrado. Ante esto, hay 5 caras en esta pirámide.
Los bordes son donde dos superficies planas se encuentran en un segmento de línea. Ante esto, hay 8 aristas en esta pirámide. Los bordes se unen en un vértice. Hay cinco vértices en esta pirámide.
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre Gayle y las fotos para su ensayo fotográfico.
Gayle ya recortó e imprimió las 12 fotos que formarán parte del proyecto de la clase de biología. Las 12 fotos estarán enmarcadas en marcos en forma de cubo. Gayle tiene que averiguar cuántos fotogramas necesita para las 12 fotos. Para ello, debe determinar cuántas caras hay en un cubo.
Solución
Para ello, Gayle necesita visualizar primero un cubo.
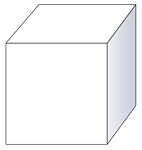
A continuación, Gayle puede usar la definición de un cubo para determinar cuántas caras o planos hay o puede contar los planos ella misma.
Un cubo es un caso especial de un prisma rectangular, lo que significa que tiene dos bases planas congruentes y cuatro planos o caras planas. Esto significa que hay un total de 6 planos planos en un cubo.
12 dividido por 6 es 2.
La respuesta es que Gayle necesita 2 cubos de fotos para mostrar las 12 fotos.
Ejemplo\(\PageIndex{2}\)
Responda la siguiente pregunta sobre la figura sólida a continuación.
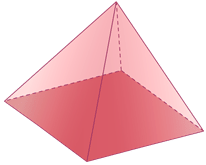
¿Cuántos bordes, caras y vértices hay en esta figura?
Solución
Primero, cuente los bordes, que serán segmentos de línea.
Hay 8 segmentos de línea, por lo que hay 8 bordes.
A continuación, cuente las caras, que serán superficies planas o planos planos.
Hay 5 planos, por lo que hay 5 caras.
Después, cuente los vértices, que son puntos o esquinas donde se encuentran varias aristas o caras.
Ahí 5 puntos, por lo que hay 5 vértices.
La respuesta es, hay cinco vértices, cinco caras y ocho aristas.
Ejemplo\(\PageIndex{3}\)
¿Cómo se llaman los puntos en una figura sólida?
Solución
Primero, recordemos que los puntos son los lugares donde se encuentran más de dos caras.
La respuesta son los vértices.
Ejemplo\(\PageIndex{4}\)
¿Cómo se llama el lugar donde se encuentran dos caras?
Solución
Primero, recordemos que cuando dos caras se encuentran, forman un segmento de línea.
La respuesta es una ventaja.
Ejemplo\(\PageIndex{5}\)
¿Cómo se llaman los lados planos de una figura?
Solución
En primer lugar, recordemos que a los lados planos también se les llama planos.
La respuesta son las caras.
Revisar
Identificar la parte de cada sólido indicado por la flecha.
-
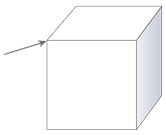
Figura\(\PageIndex{8}\) -
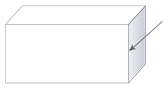
Figura\(\PageIndex{9}\) -
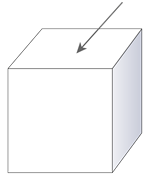
Figura\(\PageIndex{10}\)
Responde cada una de las siguientes preguntas sobre las partes de una figura sólida.
- Definir cara.
- Definir borde.
- Definir vértice.
- ¿Cuántos bordes hay en un cubo?
- ¿Qué figuras de plano conforman las caras de una pirámide cuadrada?
- ¿Qué figuras planas conforman las caras de un prisma rectangular?
- ¿Cuántos vértices hay en una pirámide triangular?
Identificar cada figura.
-
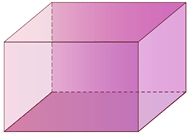
Figura\(\PageIndex{11}\) -
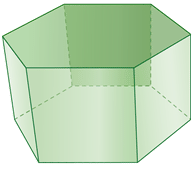
Figura\(\PageIndex{12}\) -

Figura\(\PageIndex{13}\) -
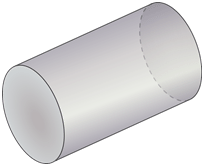
Figura\(\PageIndex{14}\) -
Figura\(\PageIndex{15}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.13.
El vocabulario
| Término | Definición |
|---|---|
| Cono | Un cono es una figura tridimensional sólida con una base circular y un vértice. |
| Cilindro | Un cilindro es una figura sólida con dos bases circulares congruentes paralelas. |
| Edge | Un borde es la intersección entre dos caras de una figura. Una arista es un segmento de línea. |
| Rostro | Una cara es una de las superficies planas de una figura sólida. |
| Figura Plane | Una figura plana es una figura plana, bidimensional. |
| Prisma | Un prisma es un objeto tridimensional con dos bases paralelas congruentes que son polígonos. |
| Pyramid | Una pirámide es un objeto tridimensional con una base que es un polígono y caras triangulares que se encuentran en un vértice. |
| Figura Sólida | Una figura sólida es una figura tridimensional con altura, anchura y profundidad. |
| Esfera | Una esfera es un sólido redondo y tridimensional. Todos los puntos de la superficie de una esfera son equidistantes del centro de la esfera. |
| Vértice | Un vértice es una esquina de un objeto tridimensional. Es el punto donde se encuentran tres o más caras. |
Recursos adicionales
Elemento Interactivo
Video: Poliedros - Caras, Vértices, Bordes
Práctica: Caras, aristas y vértices de sólidos
Mundo real: conos en erupción

