9.27: Volumen de Esferas
- Page ID
- 107303
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
María tiene un pisapapeles que es una esfera de vidrio. La esfera está llena de líquido. Si el diámetro del pisapapeles es de 6 pulgadas, ¿cuánto líquido contiene?
En este concepto, aprenderás a calcular el volumen de esferas.
Volumen
El volumen es la medida del espacio tridimensional que ocupa una figura. También se puede pensar en ello como cuánto espacio “retiene” la figura.
Para encontrar el volumen de esferas, puedes usar pirámides. Imagina una pirámide con su base en la superficie de la esfera y su punto como centro de la esfera. El radio de la esfera sería la altura de la pirámide.
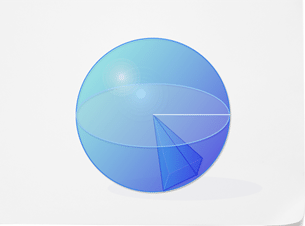
La pirámide constituye una porción del volumen de la esfera. Si puedes llenar toda la esfera con pirámides como esta, conocerías el volumen de la esfera. Sería igual a los volúmenes de todas las pirámides reunidas. ¿Cuántas pirámides se necesitarían para llenar una esfera? Eso depende de la superficie de la esfera.
Se puede combinar el área de superficie de una esfera con la fórmula de volumen de una pirámide para calcular el volumen de todas las pirámides contenidas dentro de la esfera.
La fórmula para el volumen de una pirámide es\(V=\dfrac{1}{3}Bh\).
Sabes que la altura de la pirámide es el radio (r) de la esfera y la base de la pirámide es la superficie de la esfera (\(SA=4\pi r^2\)). Si sustituye esta información en la fórmula para el volumen de una pirámide, obtendría lo siguiente.
\(\begin{aligned}V&=\dfrac{1}{3}Bh \\ V&=\dfrac{1}{3}(4\pi r^{2})r \\ V&=\dfrac{4}{3} \pi r^{3}\end{aligned}\)
El volumen de una esfera se puede encontrar usando la fórmula
\(V=\dfrac{4}{3}\pi r^{3}\)
Nuevamente, todo lo que necesitas saber es el radio de la esfera. Pones el valor en para r en la fórmula y resolver para\(V\), el volumen.
Veamos un ejemplo.
Encuentra el volumen de la esfera a continuación.
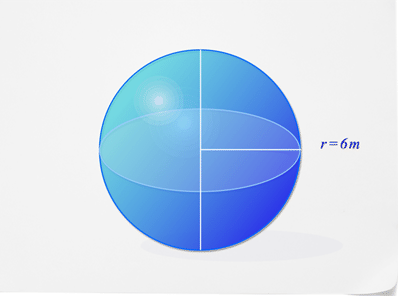
Primero, sustituya lo que sabes en la fórmula de volumen.
\(\begin{aligned} V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (6)^{3}\end{aligned}\)
A continuación, utilice álgebra para calcular el volumen.
\(\begin{aligned} V&=\dfrac{4}{3}\pi (6)^{3} \\ V&=\dfrac{4}{3}\pi (216) \\ V&=288\pi \\ V&=904.78\end{aligned}\)
La respuesta es 904.78.
El volumen de la esfera es\(904.78 \text{ m}^{3}\).
Si quisieras hacer tu medición más precisa, podrías decir que el volumen es\(288\pi m^{3}\).
Ejemplo\(\PageIndex{1}\)
Antes, te dieron un problema sobre el pisapapeles líquido de María.
María tiene un pisapapeles con un diámetro de 6 pulgadas que está lleno de agua, y quiere saber cuánto líquido hay en su interior.
Solución
Primero, encuentra el radio de la esfera. Recuerda que el radio es la mitad del diámetro.
\(\begin{aligned}r&=\dfrac{d}{2} \\ r&=\dfrac{6}{2} \\ r&=3 \end{aligned}\)
A continuación, sustituya lo que sabes en la fórmula de volumen.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (3)^{3}\end{aligned}\)
Después, usa álgebra para calcular el volumen.
\(\begin{aligned} V&=\dfrac{4}{3}\pi (3)^{3} \\ V&=\dfrac{4}{3}\pi \\ V&=(27)^{3}6\pi \\ V&=113.10v\end{aligned}\)
La respuesta es 113.10.
El volumen contenido en el pisapapeles de María es\(113.10 \text{ in}^{3}\) o\(36\pi \text{ in}^{3}\).
Ejemplo\(\PageIndex{2}\)
Encuentra el volumen de la siguiente esfera.

Solución
Primero, sustituya lo que sabes en la fórmula de volumen.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (8)^{3}\end{aligned}\)
A continuación, utilice álgebra para calcular el volumen.
\(\begin{aligned}V&=\dfrac{4}{3}\pi (8)^{3} \\ V&=\dfrac{4}{3}\pi (512) \\ V&=682.67\pi \\ V&=2144.66\end{aligned}\)
La respuesta es 2144.66. El volumen de la esfera es\(2144.66 cm^{3}\).
Si quisieras hacer tu medición más precisa, podrías decir que el volumen es\(682.67\pi cm^3\).
Ejemplo\(\PageIndex{3}\)
Encuentra el volumen de una esfera con un radio de 4 pulgadas.
Solución
Primero, sustituya lo que sabes en la fórmula de volumen.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (4)^{3}\end{aligned}\)
A continuación, utilice álgebra para calcular el volumen.
\(\begin{aligned}V&=\dfrac{4}{3}\pi (4)^{3} \\ V&=\dfrac{4}{3}\pi (64) \\ V&=85.33\pi \\ V&=268.08\end{aligned}\)
La respuesta es 268.08.
El volumen de la esfera es\(268.08 \text{ in}^{3}\).
Ejemplo\(\PageIndex{4}\)
Encuentra el volumen de una esfera con un radio de 5 pies.
Solución
Primero, sustituya lo que sabes en la fórmula de volumen.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (5)^{3}\end{aligned}\)
A continuación, utilice álgebra para calcular el volumen.
\(\begin{aligned}V&=\dfrac{4}{3}\pi (5)^{3} \\ V&=\dfrac{4}{3}\pi (125) \\ V&=166.67\pi \\ V&=523.60\end{aligned}\)
La respuesta es 523.60.
El volumen de la esfera es\(523.60 \: ft^{3}\).
Ejemplo\(\PageIndex{5}\)
Encuentra el volumen de una esfera con un radio de 3.5 pulgadas.
Solución
Primero, sustituya lo que sabes en la fórmula de volumen.
\(\begin{aligned}V&=\dfrac{4}{3}\pi r^{3} \\ V&=\dfrac{4}{3}\pi (3.5)^{3}\end{aligned}\)
A continuación, utilice álgebra para calcular el volumen.
\(\begin{aligned} V&=\dfrac{4}{3}\pi (3.5)^{3} \\ V&=\dfrac{4}{3}\pi (42.875) \\ V&=57.17\pi \\ V&=179.59\end{aligned}\)
La respuesta es 179.59.
El volumen de la esfera es\(179.59 \text{ in}^{3}\).
Revisar
Encuentra el volumen de cada esfera. Podrá redondear a la centésima más cercana cuando sea necesario.
1. Una esfera con un radio de 3 m.
2. Una esfera con un radio de 2.5 m.
3. Una esfera con un radio de 5 pulg.
4. Una esfera con un radio de 6 pulg.
5. Una esfera con un radio de 7 pies.
6. Una esfera con un radio de 4.5 cm.
7. Una esfera con un radio de 5.5 m.
8. Una esfera con un radio de 13 mm.
9. Una esfera con un diámetro de 8 pulg.
10. Una esfera con un diámetro de 10 pies.
11. Una esfera con un diámetro de 3 m.
12. Una esfera con un diámetro de 13 m.
13. Una esfera con un diámetro de 22 pies.
Usa lo que has aprendido para resolver cada problema.
14. Una esfera tiene un diámetro de 12 pies. ¿Cuál es su volumen?
15. Kelly tiene un frasco de perfume en forma de esfera. El diámetro de la botella es de 6 pulgadas. ¿Cuánto perfume le queda a Kelly si la botella sólo está medio llena?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.15.
El vocabulario
| Término | Definición |
|---|---|
| Esfera | Una esfera es un sólido redondo y tridimensional. Todos los puntos de la superficie de una esfera son equidistantes del centro de la esfera. |
| Volumen | El volumen es la cantidad de espacio dentro de los límites de un objeto tridimensional. |
Recursos adicionales
Video: Volumen de una Esfera
Práctica: Volumen de Esferas

