2.1.1: Trigonometría de Triángulo Recto
- Page ID
- 107630
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Seno, coseno, tangente y otras relaciones de lados de un triángulo rectángulo.
Seno, coseno y tangente
La trigonometría es el estudio de las relaciones entre los lados y los ángulos de los triángulos rectos. Las patas se denominan adyacentes u opuestas dependiendo del ángulo agudo que se esté utilizando.
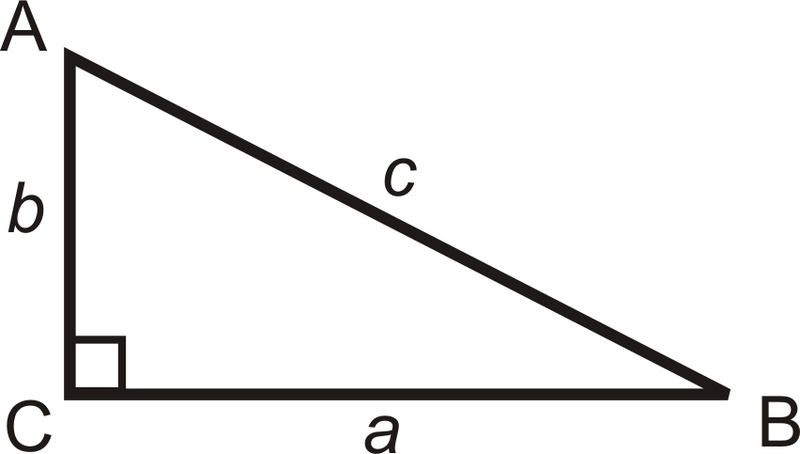
\(\begin{aligned} a \text{ is adjacent to } \angle B \qquad a \text{ is opposite } \angle A \\ b \text{ is adjacent to } \angle A \qquad b \text{ is opposite } \angle B\\ c \text{ is the hypotenuse }\end{aligned}\)
Las tres relaciones trigonométricas básicas se denominan seno, coseno y tangente. Para triángulo rectángulo ∆ABC, tenemos:
\ (\ begin {alineado}
\ text {seno Ratio:}\ dfrac {\ text {pierna opuesta}} {\ texto {hipotenusa}}\ qquad\ sin A=\ dfrac {a} {c}\ texto {o}\ sin B=\ dfrac {b} {c}\
\ text {coseno Ratio:}\ dfrac {\ texto {pierna adyacente}} {texto {hipotenusa}}\ qquad\ cos A=\ dfrac {b} {c}\ texto {o}\ cos B=\ dfrac {a} {c}\ \
\ texto {Relación tangente:}\ dfrac {\ texto {pierna opuesta}} {\ texto {pierna adyacente}}\ qquad\ tan A=\ dfrac {a} {b}\ texto {o}\ tan B=\ dfrac {b} {a}
\ end {alineado}\)
Una manera fácil de recordar las proporciones es usar SOH-CAH-TOA.
Algunos puntos importantes:
- Siempre reduce las proporciones (fracciones) cuando puedas.
- Usa el Teorema de Pitágoras para encontrar el lado faltante (si lo hay).
- Si hay un radical en el denominador, racionalizar el denominador.
¿Y si te dieran un triángulo rectángulo y te dijeran que sus lados miden 3, 4 y 5 pulgadas? ¿Cómo podrías encontrar el seno, el coseno y la tangente de uno de los ángulos no rectos del triángulo?
Encuentra el seno, coseno y proporciones tangentes de\(\angle A\).
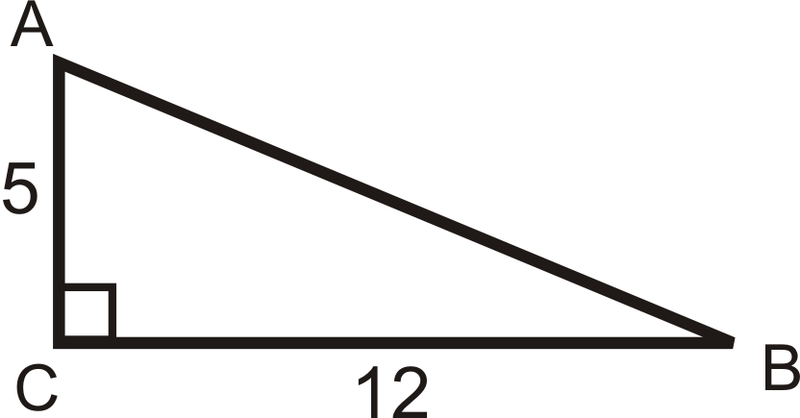
Solución
Primero, necesitamos usar el Teorema de Pitágoras para encontrar la longitud de la hipotenusa.
\ (\ begin {alineado}
5^ {2} +12^ {2} &=c^ {2}\\
13 &=c\ end {alineado}\)
\ (\ begin {alineado}
\ sin A &=\ dfrac {l e g\ texto {opuesto}\ ángulo A} {\ texto {hipotenusa}} =\ dfrac {12} {13} &\ cos A=\ dfrac {\ texto {pierna adyacente a}\ ángulo A} {\ texto {hipotenusa}} =\ dfrac {5} {13},\
\ tan\ A &=\ dfrac {\ text {pierna opuesta}\ ángulo A} {\ texto {pierna adyacente a}\ ángulo A} =\ dfrac {12} {5}
\ final {alineado}\)
Encuentra el seno, coseno, y tangente de\(\angle B\).
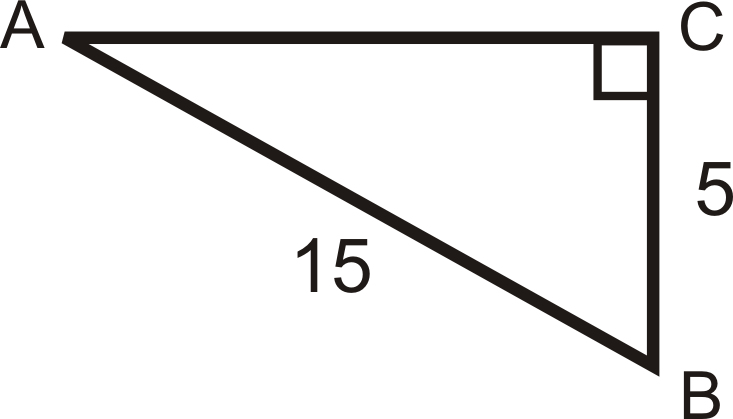
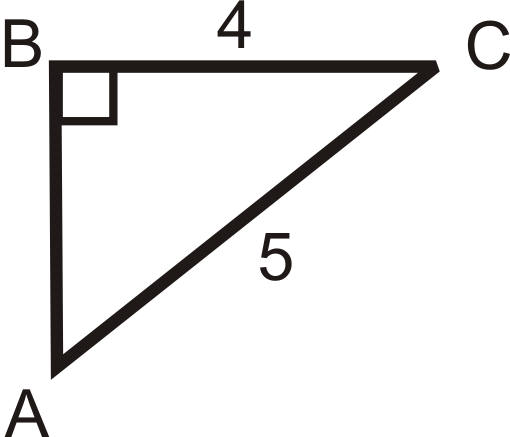
Encuentra la longitud del lado faltante.
Solución
\ (\ begin {alineado}
A C^ {2} +5^ {2} &=15^ {2}\
A C^ {2} &=200\\
A C &=10\ sqrt {2}\ end {alineado}\)
\ (\ begin {alineado}\ sin B &=\ dfrac {10\ sqrt {2}} {15} =\ dfrac {2\ sqrt {2}} {3}\ quad\ cos B=\ dfrac {5} {15} =\ dfrac {1} {3}\ quad\ tan B=\ dfrac {10\ sqrt {2}} {5} =2\ sqrt {2}
\ final {alineado}\)
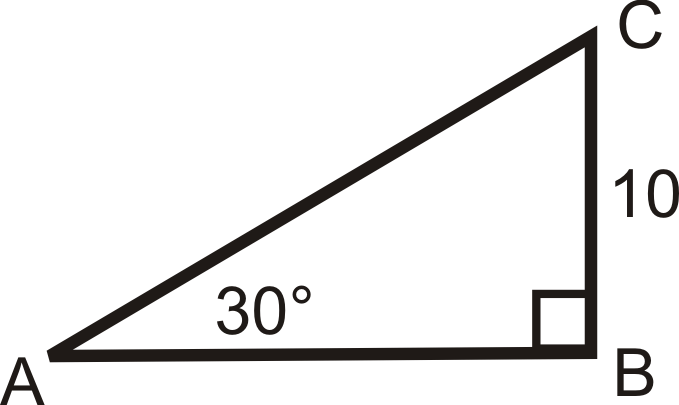
Encuentra el seno, coseno y tangente de\(30^{\circ}\).
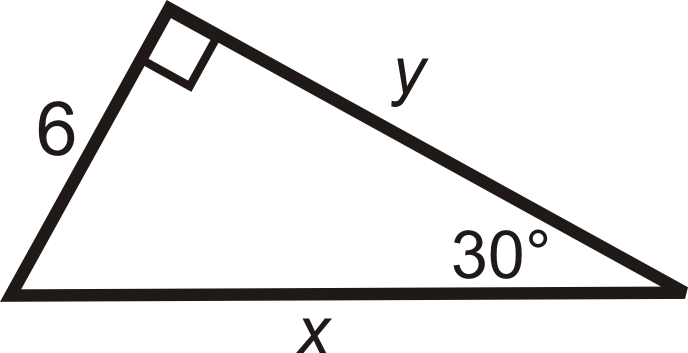
Solución
Se trata de un triángulo 30-60-90. La pierna corta es de 6,\(y=6\sqrt{3}\) y\(x=12\).
\(\sin 30^{\circ}=\dfrac{6}{12}=\dfrac{1}{2} \qquad \cos30^{\circ}=\dfrac{6\sqrt{3}}{12}=\dfrac{\sqrt{3}}{2} \qquad \tan 30^{\circ}=\dfrac{6}{6\sqrt{3}}=\dfrac{1}{\sqrt{3}}\cdot \dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
Contesta las preguntas sobre la siguiente imagen. Reducir todas las fracciones.
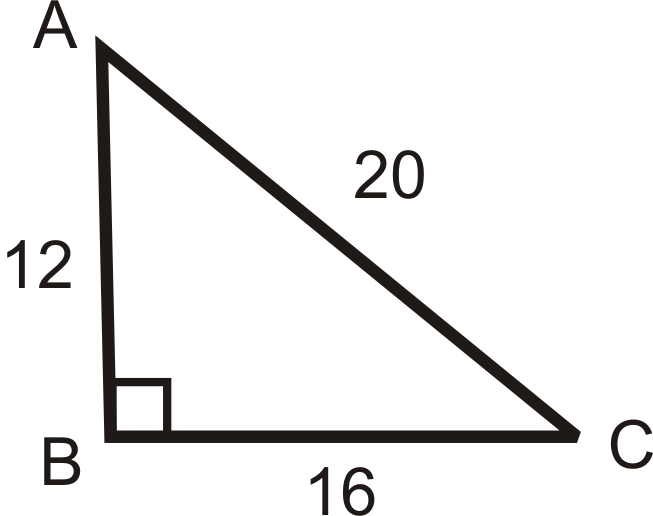
¿Qué es\(\sin A\)\(\cos A\), y\(\tan A\)?
Solución
\ (\ begin {array} {l}
\ sin A=\ dfrac {16} {20} =\ dfrac {4} {5}\
\ cos A=\ dfrac {12} {20} =\ dfrac {3} {5}\
\ tan A=\ dfrac {16} {12} =\ dfrac {4} {3}
\ end {array}\)
Revisar
Usa el diagrama para rellenar los espacios en blanco a continuación.
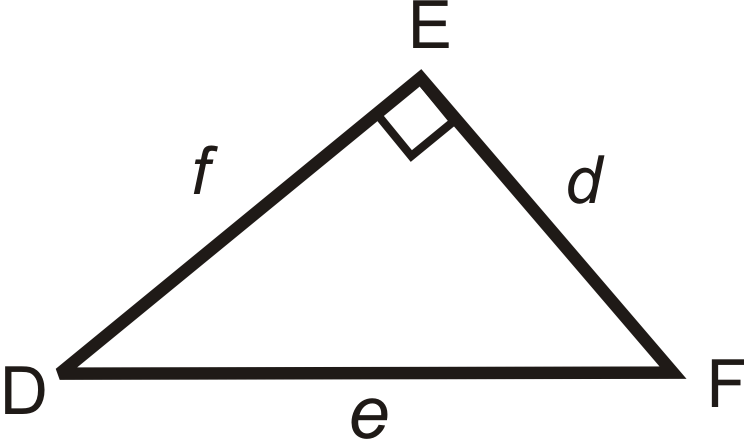
- \(\tan D=\dfrac{?}{?}\)
- \(\sin F=\dfrac{?}{?}\)
- \(\tan F=\dfrac{?}{?}\)
- \(\cos F=\dfrac{?}{?}\)
- \(\sin D=\dfrac{?}{?}\)
- \(\cos D=\dfrac{?}{?}\)
De las preguntas 1-6, podemos concluir lo siguiente. Rellene los espacios en blanco.
- \(\cos \underline{\qquad}=\sin F\)y\(\sin \underline{\qquad}=\cos F\).
- \(\tan D\)y\(\tan F\) son _________ el uno del otro.
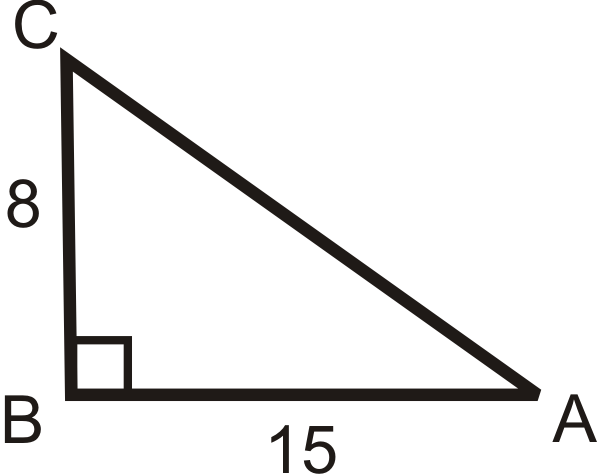
Encuentra el seno, coseno y tangente de\(\angle A\). Reducir todas las fracciones y radicales.
-
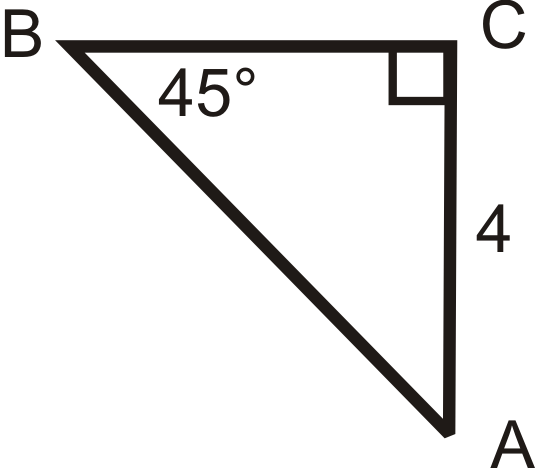
Figura\(\PageIndex{8}\) -
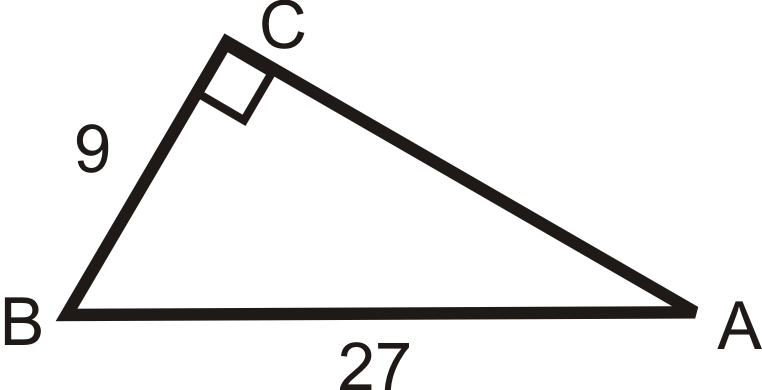
Figura\(\PageIndex{9}\) -
Figura\(\PageIndex{10}\) -
Figura\(\PageIndex{11}\) -
Figura\(\PageIndex{12}\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 8.7.
Recursos
El vocabulario
| Término | Definición |
|---|---|
| Ángulo Agudo | Un ángulo agudo es un ángulo con una medida de menos de 90 grados. |
| Ángulos adyacentes | Dos ángulos son adyacentes si comparten un lado y un vértice. La palabra 'adyacente' significa 'al lado' o 'al lado de'. |
| Hipotenusa | La hipotenusa de un triángulo rectángulo es el lado más largo del triángulo rectángulo. Está frente al ángulo recto. |
| Patas de un Triángulo Recto | Las patas de un triángulo rectángulo son los dos lados más cortos del triángulo rectángulo. Las patas están adyacentes al ángulo recto. |
| opuesto | Lo contrario de un número\(x\) es\(−x\). Un número y su opuesto siempre suman a cero. |
| Teorema de Pitágoras | El Teorema de Pitágoras es una relación matemática entre los lados de un triángulo rectángulo\(a^2+b^2=c^2\), dada por, donde a y b son patas del triángulo y c es la hipotenusa del triángulo. |
| Radical | El signo\(\sqrt\), o raíz cuadrada,. |
| seno | El seno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud de la hipotenusa. |
| Ratios trigonométricos | Ratios que nos ayudan a subestimar las relaciones entre lados y ángulos de triángulos rectos. |
Recursos adicionales
Video: Introducción a las Funciones Trigonométricas U\ sin g Triángulos
Actividades: Seno, coseno, tangente Discusión Preguntas
Ayudas de estudio: Guía de estudio de relaciones trigonométricas
Práctica: Trigonometría de Triángulo Recto
Mundo real: Tangente de coseno