2.1.3: PECADO
- Page ID
- 107602
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Relaciones trigonométricas basadas en lados de triángulos rectos en relación a un ángulo.
Entendiendo los Sines

Jacob tiene que encerrar luces alrededor de los aleros de su cobertizo de techo plano. Al tener miedo a las alturas quiere planear este empeño con mucho cuidado. Sabe que por razones de seguridad, una escalera debe hacer un ángulo de\(75^{\circ}\) o menos con el suelo. Si Jacob tiene una escalera de 6.5 metros de largo para colocar contra el costado del cobertizo que tiene 2.5 metros de altura, entonces ¿qué ángulo hará la escalera con el suelo? Jacob necesita estar seguro de que el ángulo cumple con los requisitos de seguridad antes de poner un pie en la escalera. ¿Cómo puede averiguar la medida del ángulo entre la escalera y el suelo?
En este concepto, aprenderás a entender la relación trigonométrica del seno.
Sines
La trigonometría es una rama de la matemática utilizada para determinar las longitudes de los lados y la medida de los ángulos con gran precisión. Solo considerarás los resultados obtenidos mediante el uso de triángulos rectos.
El lado de un triángulo rectángulo ubicado opuesto al ángulo 90^ {\ circ} es el lado más largo del triángulo y se llama hipotenusa. Los dos lados más cortos del triángulo, a menudo llamados patas, tienen nombres específicos en referencia a la ubicación de uno de los ángulos agudos del triángulo rectángulo.

En ambos triángulos la hipotenusa es opuesta al ángulo recto. En el primer triángulo el ángulo marcado en rojo se llama el ángulo de referencia y se usa para nombrar las patas del triángulo. La medida del ángulo de referencia puede ser dada o su medida puede tener que ser calculada. Sea cual sea el caso, uno de los ángulos agudos será referido en la pregunta o problema. El lado que cruza desde el ángulo de referencia se llama el lado opuesto. El tercer lado se llama lado adyacente y es el lado del triángulo, junto con la hipotenusa, el que forma el ángulo de referencia.
En el segundo triángulo el ángulo marcado en rojo se llama el ángulo de referencia y se usa para nombrar las patas de este triángulo. El lado que cruza desde el ángulo de referencia se llama el lado opuesto. El tercer lado se llama lado adyacente y es el lado del triángulo, junto con la hipotenusa, el que forma el ángulo de referencia.
La ubicación de la hipotenusa nunca cambia pero la ubicación de los lados opuestos y adyacentes depende de qué ángulo agudo es el ángulo de referencia.
En cada diagrama dado, etiquete cada lado del triángulo rectángulo como el:
Hipotenusa (H); Lado Ángulo de referencia opuesto (O); Lado adyacente al ángulo de referencia (A)
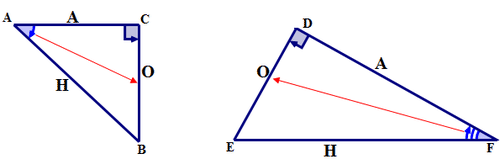
Una relación de las longitudes de los lados de un triángulo rectángulo se llama relación trigonométrica. La relación de la longitud del lado opuesto al ángulo de referencia a la longitud de la hipotenusa se conoce como la relación s ine. La relación sinusoidal está relacionada con el ángulo de referencia del triángulo recto, no con el ángulo recto.
La relación sinusoidal para el primer triángulo se puede escribir en palabras como:
seno de\(\angle A=\dfrac{\text{side opposite} \angle A}{\text{hypotenuse}}\) O en forma acortada como seno de\(\angle A=\dfrac{opposite}{hypotenuse}\)
La relación sinusoidal para el primer triángulo se puede escribir en símbolos como:
\(\sin A=\dfrac{BC}{AB}\)
La relación sinusoidal para el segundo triángulo se puede escribir en palabras como:
seno de\(\angle F=\dfrac{\text{side opposite}\angle F}{\text{hypotenuse}}\) O en forma acortada como seno de\(\angle F=\dfrac{opposite}{hypotenuse}\)
La relación sinusoidal para el primer triángulo se puede escribir en símbolos como:
\(\sin F=\dfrac{DE}{EF}\)
Determinemos el valor para la relación sinusoidal de cada uno de los ángulos agudos usando el siguiente triángulo rectángulo. Expresar la relación sinusoidal en palabras y símbolos. Después, usando los valores en los lados correspondientes, sustituya los símbolos por los números y expresen la relación primero como fracción y luego como decimal redondeado a la diez milésima más cercana (cuatro lugares después del decimal).
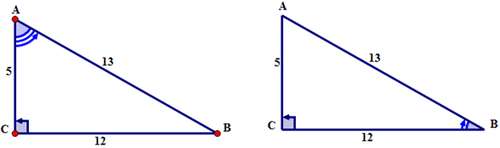
Para el primer triángulo:
Primero, con respecto al ángulo de referencia A, nombra los lados del triángulo.
La hipotenusa se encuentra frente al ángulo recto. El lado opuesto está al otro lado de\(\angle A\). El lado al lado\(\angle A\) es el adyacente. Los lados están etiquetados con las letras H, O, A respectivamente.
A continuación, escriba la relación sinusoidal para\(\angle A\) en todas las formas requeridas.
Palabras:
seno de\(\angle A=\dfrac{opposite}{hypotenuse}\)
Símbolos:
\(\sin A=\dfrac{BC}{AB}\)
Fracción:
\(\sin A=\dfrac{12}{13}\)
Decimal:
\(\sin A=0.9231\)
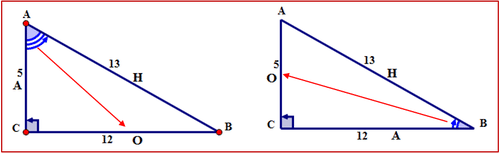
El segundo triángulo es el primer triángulo con\ ángulo B como ángulo de referencia. Observe que las ubicaciones de los lados opuestos y adyacentes han cambiado desde donde estaban cuando\ ángulo A era el ángulo de referencia.
Primero, con respecto al ángulo de referencia B, nombra los lados del triángulo.
La hipotenusa se encuentra frente al ángulo recto. El lado opuesto está al otro lado de\(\angle B\). El lado al lado\(\angle B\) es el adyacente. Los lados están etiquetados con las letras H, O, A respectivamente.
A continuación, escriba la relación sinusoidal para\(\angle B\) en todas las formas requeridas.
Palabras:
seno de\(\angle B=\dfrac{opposite}{hypotenuse}\)
Símbolos:
\(\sin B=\dfrac{AC}{AB}\)
Fracción:
\(\sin B=\dfrac{5}{13}\)
Decimal:
\(\sin B=0.3846\)
Si SINB=0.3846, entonces la medida de\ ángulo B se puede encontrar usando la calculadora TI-84.
Recuerda que mides ángulos en unidades llamadas grados. Presiona el modo y mira la pantalla.
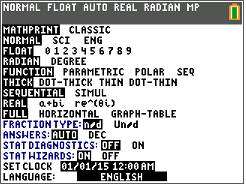
En la cuarta fila de la pantalla, GRADO no se resalta.
Sigue el Historial de Prensa Clave a continuación para poner la calculadora en modo GRADO.
 Figura\(\PageIndex{7}\)
Figura\(\PageIndex{7}\)En la cuarta fila de la pantalla, ahora se resalta GRADO.
A continuación, siga el Historial de Prensa Clave a continuación para encontrar la medida de\(\angle B\).
Luego, mira la pantalla de la calculadora:
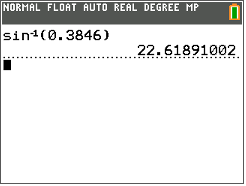
Redondea la medida del ángulo a la décima más cercana.
\(\angle B=22.6^{\circ}\)
La respuesta es\(22.6^{\circ}\)
Antes, te dieron un problema sobre Jacob y el ángulo de su escalera. Jacob necesita asegurarse de que la escalera hace un ángulo de menos que\(75^{\circ}\) con el suelo? Jacob tendrá que usar la relación sinusoidal para resolverlo.
Solución
Primero, dibuja y etiqueta un triángulo rectángulo con la información dada.
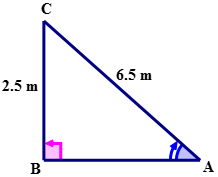
A continuación, nombra los lados del triángulo con referencia a\(\angle A\).
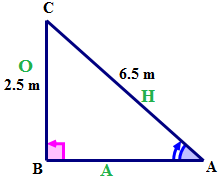
A continuación, exprese la proporción\(\sin A\) usando palabras.
\(\sin A=\dfrac{opposite}{hypotenuse}\)
A continuación, exprese la relación usando símbolos.
\(\sin A=\dfrac{BC}{AC}\)
A continuación, expresar la relación como una fracción utilizando los valores correspondientes de los lados.
\(\sin A=\dfrac{2.5}{6.5}\)
A continuación, exprese la relación como decimal.
\(\sin A=0.3846\)
A continuación, use la función sen−1 en la calculadora TI para encontrar la medida de\ ángulo A.
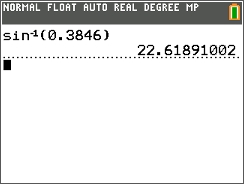
Después, escribe la medida de\(\angle A\) a la décima más cercana.
\(\angle A=22.6^{\circ}\)
La respuesta es\(22.6^{\circ}\).
Es seguro que Jacob suba por la escalera.
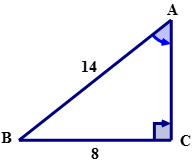
Usa la relación sinusoidal para calcular la medida de\(\angle A\) hasta la décima más cercana.
Solución
Primero, usando\(\angle A\) nombre los lados del triángulo.
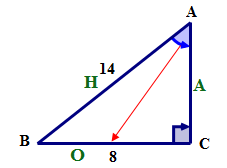
A continuación, escribe la relación sinusoidal en palabras.
\(\sin A=\dfrac{opposite}{hypotenuse}\)
A continuación, escribe la relación usando símbolos.
\(\sin A=\dfrac{BC}{AB}\)
A continuación, expresar la relación como fracción utilizando los valores de los lados correspondientes.
\(\sin A=\dfrac{8}{14}\)
A continuación, exprese la relación como decimal redondeado a cuatro lugares después del decimal.
\(\sin A=0.5714\)
Luego, use la función sinusoidal inversa (\(\sin^{−1}\)) en la calculadora TI para encontrar la medida de\(\angle A\).
Después, mira la pantalla y redondea la medida del ángulo a la décima más cercana.
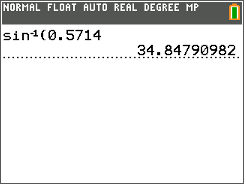
Observe, no es necesario cerrar el paréntesis después de que se haya ingresado el decimal en la calculadora.
\(\angle A=34.9^{\circ}\)
La respuesta es\(34.9^{\circ}\)
Para el siguiente triángulo rectángulo, exprese el SinB en palabras, símbolos, como fracción y como decimal.
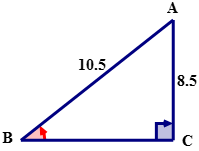
Solución
Primero, nombra los lados del triángulo usando el ángulo de referencia B.
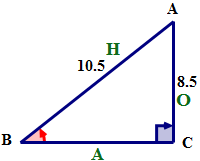
A continuación, exprese la relación SinB usando palabras.
\(\sin B=\dfrac{opposite}{hypotenuse}\)
A continuación, exprese la relación usando símbolos.
\(\sin B=\dfrac{AC}{AB}\)
A continuación, expresar la relación como una fracción utilizando los valores correspondientes de los lados.
\(\sin B=\dfrac{8.5}{10.5}\)
Entonces, expresar la relación como decimal a la diez milésima.
\(\sin B=0.8095\)
La respuesta es 0.8095.
Si\(\sin A=0.3872\), cuál es la medida de\(\angle A\) al décimo más cercano.
Solución
Primero, use la calculadora TI y siga el historial de pulsaciones de teclas.
A continuación, mira la pantalla de la calculadora.
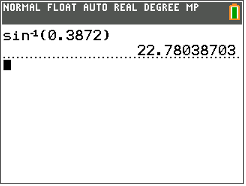
Después, escribe la medida de\(\angle A\) a la décima más cercana.
\(\angle A=22.8^{\circ}\)
La respuesta es\(22.8^{\circ}\).
Determinar la medida de\ ángulo B en el siguiente triángulo.
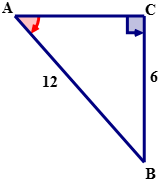
Solución
Primero, nombra los lados del triángulo.
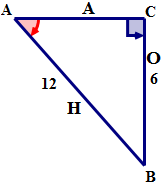
A continuación, exprese la relación pecado A usando palabras.
\(sin A=\dfrac{opposite }{hypotenuse}\)
A continuación, exprese la relación usando símbolos.
\(\sin A=\dfrac{BC}{AB}\)
A continuación, expresar la relación como una fracción utilizando los valores correspondientes de los lados.
\(\sin A=\dfrac{6}{12}\)
A continuación, exprese la relación como decimal.
\(\sin A=0.5\)
A continuación, utilice la función sin−1 en la calculadora TI para encontrar la medida de\(\angle A\).
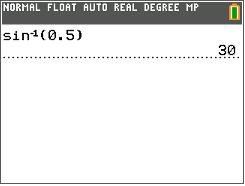
Entonces, escribe la medida de\(\angle A\).
\(\angle A=30^{\circ}\)
La respuesta es\(30^{\circ}\).
Revisar
Resuelve cada problema.
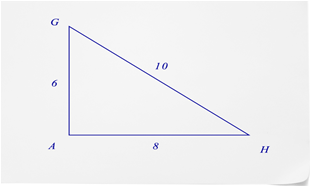
- ¿De qué es el seno\(\angle G\)?
- ¿De qué es el seno\(\angle H\)?
- ¿Puedes encontrar el seno de\(\angle A\)?
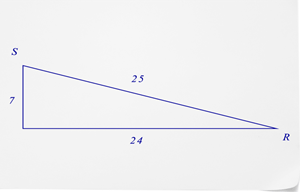
- ¿De qué es el seno\(\angle R\)?
- ¿De qué es el seno\(\angle S\)?
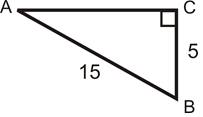
- ¿De qué es el seno\(\angle A\)?
- ¿De qué es el seno\(\angle B\)?
- ¿Cuál es la longitud del lado faltante redondeado a la centésima más cercana?
Responder a cada pregunta verdadera o falsa.
- Puedes usar el Teorema de Pitágoras para encontrar la longitud de un lado faltante en un triángulo rectángulo.
- Un triángulo rectángulo debe tener un ángulo de 90 grados.
- La relación sinusoidal es la hipotenusa sobre el lado opuesto.
- Si solo conoces la longitud lateral, entonces puedes averiguar todas las longitudes de los lados.
- La relación sinusoidal tiene que ver con longitudes laterales.
- La hipotenusa siempre es opuesta al ángulo recto.
- Se le deben dar las tres longitudes de lado para averiguar la relación sinusoidal.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.13.
vocabulario
| Término | Definición |
|---|---|
| seno | El seno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud de la hipotenusa. |
| Relaciones trigonométricas | Ratios que nos ayudan a entender las relaciones entre lados y ángulos de triángulos rectos. |
Recursos adicionales
Video: Introducción a las funciones trigonométricas mediante triángulos
Actividades: Razones trigonométricas con una calculadora Preguntas de discusión
Práctica: Calculadora de funciones trigonométricas
Mundo Real: Tangente Sine Cosine

