2.1.6: TAN
- Page ID
- 107612
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Explora la relación tangente y úsala para encontrar los lados faltantes de los triángulos rectos.
A medida que la medida de un ángulo aumenta entre\(0^{\circ}\) y\(90^{\circ}\), ¿cómo cambia la relación tangente del ángulo?
Relación tangente
Recordemos que una forma de mostrar que dos triángulos son similares es mostrar que tienen dos pares de ángulos congruentes. Esto significa que dos triángulos rectos serán similares si tienen un par de ángulos no rectos congruentes.
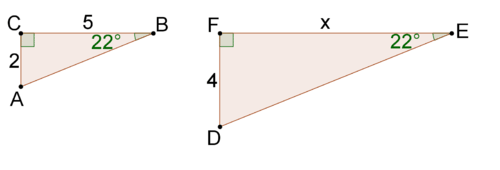
Los dos triángulos rectos anteriores son similares porque tienen dos pares de ángulos congruentes. Esto quiere decir que sus lados correspondientes son proporcionales. \(\overline{DF}\)y\(\overline{AC}\) son lados correspondientes porque ambos son opuestos al\(22^{\circ}\) ángulo. \(\dfrac{DF}{AC}=\dfrac{4}{2}=2\), por lo que el factor de escala entre los dos triángulos es 2. Esto significa que\(x=10\), porque\(\dfrac{FE}{CB}=\dfrac{10}{5}=2\).
La relación entre las dos patas de cualquier\(22^{\circ}\) triángulo rectángulo siempre será la misma, porque todos los\(22^{\circ}\) triángulos rectos son similares. La relación entre la longitud de la pierna opuesta al\(22^{\circ}\) ángulo con la longitud de la pata adyacente al\(22^{\circ}\) ángulo será\(\dfrac{2}{5}=0.4\). Puedes usar este hecho para encontrar un lado faltante de otro\(22^{\circ}\) triángulo rectángulo.
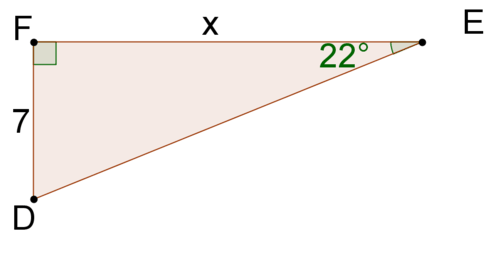
Porque esto es un\(22^{\circ}\) triángulo rectángulo, ya lo sabes\(\dfrac{\text{opposite leg}}{\text{adjacent leg}}=\dfrac{2}{5}=0.4\).
\(\begin{aligned} \dfrac{\text{opposite leg}}{\text{adjacent leg}}&=0.4 \\ \dfrac{7}{x}&=0.4 \\ 0.4x &=7\\ x&=17.5 \end{aligned}\)
La relación entre la pata opuesta y la pata adyacente para un ángulo dado en un triángulo rectángulo se llama relación tangente. Tu calculadora científica o gráfica tiene tangente programada en ella, para que puedas determinar la relación\ dfrac {\ text {pierna opuesta}} {\ text {pierna adyacente}}\) para cualquier ángulo dentro de un triángulo rectángulo. La abreviatura de tangente es tan.
Cálculo de funciones tangentes
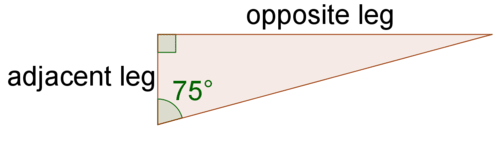
Usa tu calculadora para encontrar la tangente de\(75^{\circ}\). ¿Qué representa este valor?
Asegúrate de que tu calculadora esté en modo grados. Entonces, escriba “\(\tan(75)\)”.
\(tan(75^{\circ})\approx 3.732\)
Esto significa que la relación de la longitud de la pata opuesta a la longitud de la pata adyacente para un\(75^{\circ}\) ángulo dentro de un triángulo rectángulo será de aproximadamente 3.732.
Resolviendo valores desconocidos
1. Resolver para\(x\).
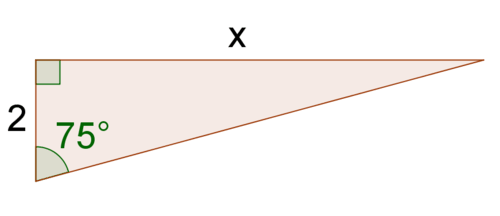
Del problema anterior, ya sabes que la proporción\(\dfrac{\text{opposite leg}}{\text{adjacent leg}} \approx 3.732\). Puedes usar esto para resolver para\(x\).
\ (\ begin {alineado}
\ dfrac {\ text {pierna opuesta}} {\ text {pierna adyacente}} &\ approx 3.732\
\ dfrac {x} {2} &\ approx 3.732\\
x &\ aproximadamente 7.464
\ final {alineado}\)
2. Resolver para\(x\) y\(y\).
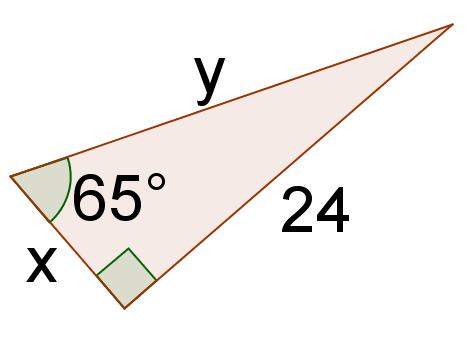
Puedes usar el\(65^{\circ}\) ángulo para encontrar la relación correcta entre 24 y\(x\).
\ (\ begin {alineado}
\ tan\ izquierda (65^ {\ circ}\ derecha) &=\ dfrac {\ text {pierna opuesta}} {\ text {pierna adyacente}}\\
2.145 &\ approx\ dfrac {24} {x} {x}\\
x &\ approx\ dfrac {24} {2.145}\
x &\ approx 11.189
\ fin {alineado}\)
Tenga en cuenta que esta respuesta es sólo aproximada porque redondeó el valor de\(\tan 65^{\circ}\). Una respuesta exacta incluirá “bronceado”. La respuesta exacta es:
\(x=\dfrac{24}{\tan 65^{\circ}}\)
Para resolver por y, puedes usar el Teorema de Pitágoras porque se trata de un triángulo rectángulo.
\ (\ begin {array} {r}
11.189^ {2} +24^ {2} =y^ {2}\\
701.194=y^ {2}\\
26.48=y
\ end {array}\)
Anteriormente, se le preguntó cómo cambia la relación tangente del ángulo.
Solución
A medida que la medida de un ángulo aumenta entre\(0^{\circ}\) y\(90^{\circ}\), ¿cómo cambia la relación tangente del ángulo?

A medida que aumenta un ángulo, aumenta la longitud de su pata opuesta. Por lo tanto,\(\dfrac{\text{opposite leg}}{\text{adjacent leg}}\) aumenta y así aumenta el valor de la relación tangente.
Tangente te indica la relación de las dos patas de un triángulo rectángulo con un ángulo dado. ¿Por qué la relación tangente no funciona de la misma manera para triángulos no rectos?
Solución
Dos triángulos rectos con un\(32^{\circ}\) ángulo serán similares. Dos triángulos no rectos con un\(32^{\circ}\) ángulo no necesariamente serán similares. La relación tangente funciona para triángulos rectos porque todos los triángulos rectos con un ángulo dado son similares. La relación tangente no funciona de la misma manera para triángulos no rectos porque no todos los triángulos no rectos con un ángulo dado son similares. Solo se puede usar la relación tangente para triángulos rectos.
Usa tu calculadora para encontrar la tangente de\(45^{\circ}\). ¿Qué representa este valor? ¿Por qué tiene sentido este valor?
Solución
\(\tan(45^{\circ})=1\). Esto significa que la relación entre la longitud de la pata opuesta y la longitud de la pata adyacente es igual a 1 para los triángulos rectos con un\(45^{\circ}\) ángulo.
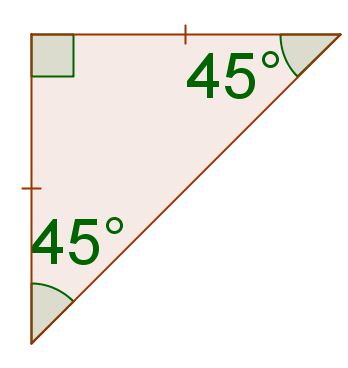
Esto debería tener sentido porque los triángulos rectos con un\(45^{\circ}\) ángulo son isósceles. Las patas de un triángulo isósceles son congruentes, por lo que la relación entre ellas será de 1.
Resolver para\(x\).
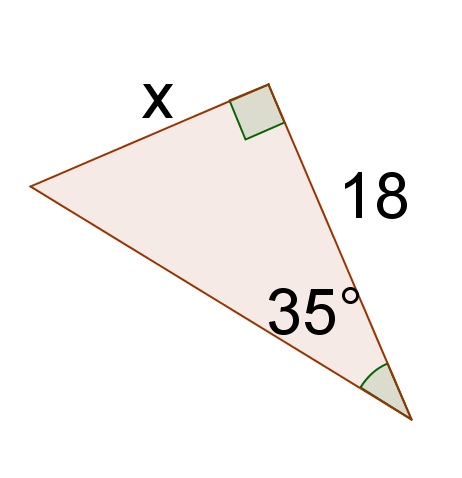
Solución
Utilice la relación tangente de un\(35^{\circ}\) ángulo.
\ (\ begin {alineado}
\ tan\ izquierda (35^ {\ circ}\ derecha) &=\ dfrac {\ text {pierna opuesta}} {\ text {pierna adyacente}}\\
\ tan\ izquierda (35^ {\ circ}\ derecha) &=\ dfrac {x} {18}\\
x &=18\ tan\ izquierda (35^ {\ circ}\ derecha)\\
x &\ aprox 12.604
\ fin { alineado}\)
Revisar
1. ¿Por qué todos los triángulos rectos con un\(40^{\circ}\) ángulo son similares? ¿Qué tiene que ver esto con la relación tangente?
2. Encuentra la tangente de\(40^{\circ}\).
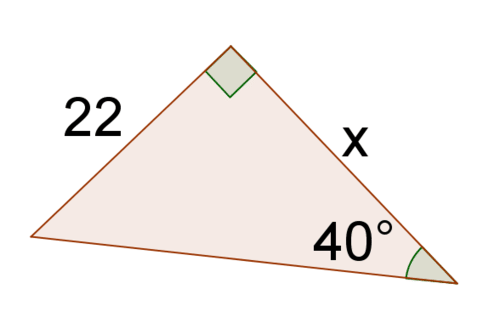
3. Resolver para\(x\).
4. Encuentra la tangente de\(80^{\circ}\).
5. Resolver para\(x\).
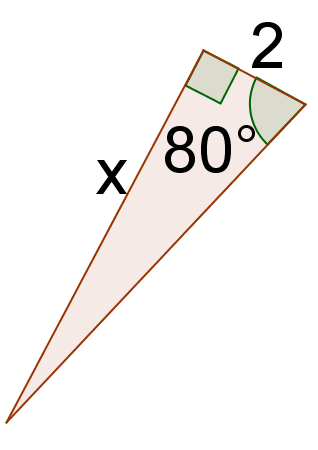
6. Encuentra la tangente de\(10^{\circ}\).
7. Resolver para\(x\).
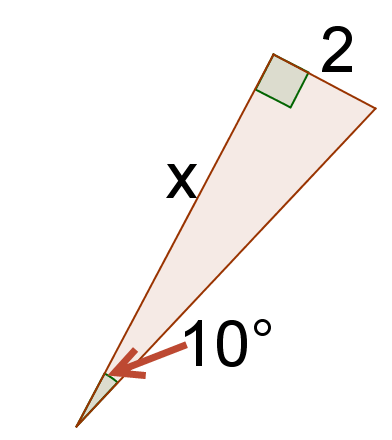
8. Tu respuesta a #5 debe ser la misma que tu respuesta a #7. ¿Por qué?
9. Encuentra la tangente de\(27^{\circ}\).
10. Resolver para\(x\).
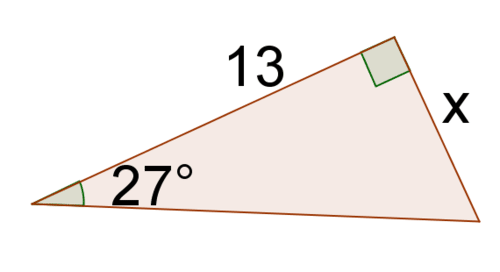
11. Encuentra la tangente de\(42^{\circ}\).
12. Resolver para\(x\).
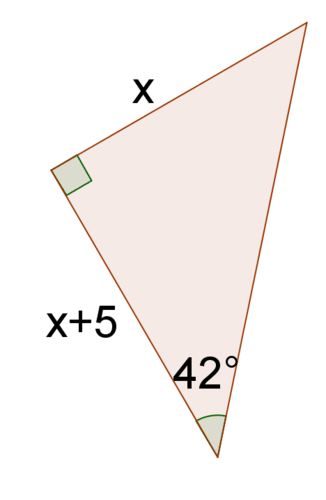
13. Un triángulo rectángulo tiene un\(42^{\circ}\) ángulo. La base del triángulo, adyacente al\(42^{\circ}\) ángulo, es de 5 pulgadas. Encuentra el área del triángulo.
14. Recordemos que las relaciones entre los lados de un triángulo 30-60-90 son\(1:\sqrt{3}:2\). Encuentra la tangente de\(30^{\circ}\). Explica cómo esto coincide con las proporciones para un triángulo 30-60-90.
15. Explique por qué tiene sentido que el valor de la relación tangente aumente a medida que el ángulo va de\(0^{\circ}\) a\(90^{\circ}\).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.1.
El vocabulario
| Término | Definición |
|---|---|
| Postulado de similitud AA | Si dos ángulos en un triángulo son congruentes con dos ángulos en otro triángulo, entonces los dos triángulos son similares. |
| Congruente | Las figuras congruentes son idénticas en tamaño, forma y medida. |
| Similares | Dos figuras son similares si tienen la misma forma, pero no necesariamente del mismo tamaño. |
| Tangente | La tangente de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud del lado adyacente al ángulo dado. |

