2.1.4: COS
- Page ID
- 107616
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Determinar las longitudes de lado dadas por coseno
Comprensión de los cosenos

Roger ha colocado una escalera que mide 12 pies de largo contra el costado de la casa de tal manera que el pie de la escalera está a 5 pies de la base de la casa. Mientras Roger se prepara para subir la escalera para limpiar las canaletas de lluvia de la casa, su vecino le grita: “Es mejor que hayas ajustado esa escalera. El ángulo entre la escalera y el suelo tiene que ser menor que\(75^{\circ}\).”
Roger dio un paso atrás y miró la posición de la escalera. “Podría tener razón”, pensó Roger. “Tengo que averiguar el tamaño de ese ángulo antes de subir esa escalera”.
¿Cómo puede Roger calcular la medida del ángulo?
En este concepto, aprenderás a entender la relación trigonométrica Coseno.
Coseno
La trigonometría es una rama de la matemática utilizada para determinar las longitudes de los lados y la medida de los ángulos con gran precisión. Una relación de las longitudes de los lados de un triángulo rectángulo se llama relación trigonométrica. La relación de la longitud del lado junto con el ángulo de referencia a la longitud de la hipotenusa se conoce como la relación coseno. Un ángulo agudo de un triángulo rectángulo está formado por la hipotenusa y una de las patas del triángulo. Esta pata se llama el lado adyacente del ángulo de referencia. La relación coseno es la relación del lado adyacente a la hipotenusa.
En cada diagrama dado, etiquete cada lado del triángulo rectángulo como el:
Hipotenusa (H); Lado Ángulo de referencia opuesto (O); Lado Adyacente al ángulo de referencia (A).
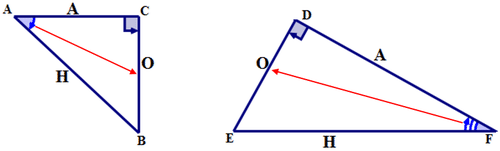
La relación coseno para el primer triángulo se puede escribir en palabras como:
coseno de\(\angle A=\dfrac{\text{side adjacent }\angle A}{\text{hypotenuse}}\) O en forma abreviada como coseno de\(\angle A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
La relación coseno para el primer triángulo se puede escribir en símbolos como:
\(\cos A=\dfrac{AC}{AB}\)
La relación coseno para el segundo triángulo se puede escribir en palabras como:
coseno de\(\angle F = \dfrac{\text{side adjacent }\angle F}{\text{hypotenuse}}\) O en forma abreviada como coseno de\(\angle F=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
La relación coseno para el segundo triángulo se puede escribir en símbolos como:
\(\cos F=\dfrac{DF}{EF}\)
Determinemos el valor para la relación coseno de cada uno de los ángulos agudos usando el siguiente triángulo rectángulo. Expresar la relación coseno en palabras y símbolos. Después, usando los valores en los lados correspondientes, sustituya los símbolos por los números y expresen la relación primero como fracción y luego como decimal redondeado a la diez milésima más cercana (cuatro lugares después del decimal).
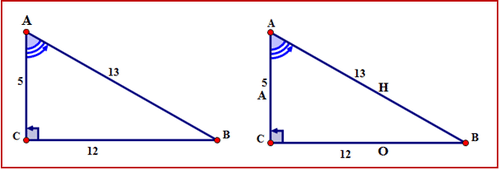
\(\Delta ABC\)con\(\angle A\) como el ángulo de referencia.
Primero, nombra los lados del triángulo.
La hipotenusa se encuentra frente al ángulo recto. El lado opuesto está al otro lado de\ ángulo A. El lado al lado\ ángulo A es el adyacente. Los lados están etiquetados con las letras H, O, A respectivamente.
A continuación, escriba la relación coseno para\(\angle A\) en todas las formas requeridas.
Palabras:
coseno de\(\angle A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Símbolos:
\(\cos A=\dfrac{AC}{AB}\)
Fracción:
\(\cos A=\dfrac{5}{13}\)
Decimal:
\(\cos A=0.3846\)
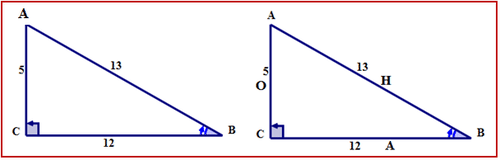
\(\Delta ABC\)con\(\angle B\) como el ángulo de referencia.
Observe que las ubicaciones de los lados opuestos y adyacentes han cambiado desde donde estaban cuando\(\angle A\) era el ángulo de referencia.
Primero, nombra los lados del triángulo.
La hipotenusa se encuentra frente al ángulo recto. El lado opuesto está al otro lado de\(\angle B\). El lado al lado\(\angle B\) es el adyacente. Los lados están etiquetados con las letras H, O, A respectivamente.
A continuación, escriba la relación coseno para\(\angle B\) en todas las formas requeridas.
Palabras:
coseno de\(\angle B=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
Símbolos:
\(\cos B=\dfrac{BC}{AB}\)
Fracción:
\(\cos B=\dfrac{12}{13}\)
Decimal:
\(\cos B=0.9231\)
Si\(\cos A=0.3846\), entonces la medida de se\(\angle A\) puede encontrar usando la función de coseno inverso en la calculadora TI-.
Primero, siga el Historial de Prensa Clave a continuación para calcular la medida de\(\angle A\).
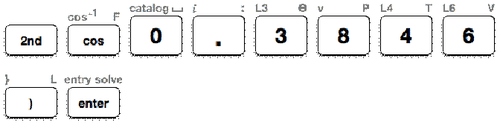
A continuación, mira la pantalla de la calculadora para ver la medida de\(\angle A\).
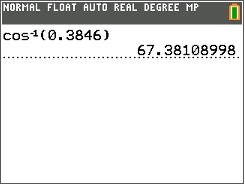
Después, escribe la medida de\(\angle A\) a la décima más cercana.
\(\angle A=67.4^{\circ}\)
La respuesta es\(67.4^{\circ}\)
Antes, te dieron un problema sobre Roger y la escalera. Necesita averiguar el ángulo que hace la escalera con el suelo.
¿Cómo puede Roger averiguar la medida del ángulo?
Solución
Él puede usar la relación coseno.
Primero, dibuje y etiquete un triángulo rectángulo para modelar el problema.
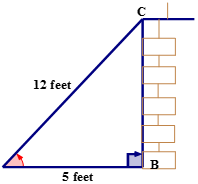
A continuación, nombra los lados del triángulo.
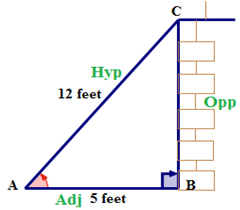
A continuación, escriba la relación coseno en palabras.
\(\cos A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
A continuación, escribe la relación usando símbolos.
\(\cos A=\dfrac{AB}{AC}\)
A continuación, expresar la relación como fracción utilizando los valores de los lados correspondientes.
\(\cos A=\dfrac{5}{12}\)
A continuación, exprese la relación como decimal redondeado a cuatro lugares después del decimal.
\(\cos A=0.4167\)
A continuación, utilice la función coseno inverso (cos−1) en la calculadora TI para encontrar la medida de\(\angle A\).
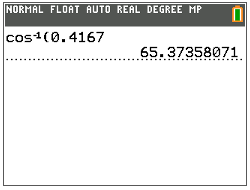
Después, escribe la medida de\(\angle A\) a la décima más cercana.
\(\angle A=65.4^{\circ}\)
La respuesta es\(65.4^{\circ}\)
La medida de\(\angle A\) es\(65.4^{\circ}\). Es menos que\(75^{\circ}\) así Roger puede reparar las canaletas de lluvia.
Use la relación coseno para calcular la medida de\(\angle A\) al décimo más cercano.
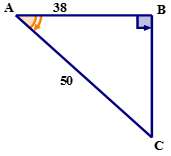
Solución
Primero, usando el ángulo de referencia nombra los lados del triángulo.
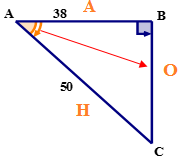
A continuación, escriba la relación coseno en palabras.
\(\cos A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
A continuación, escribe la relación usando símbolos.
\(\cos A=\dfrac{AB}{AC}\)
A continuación, expresar la relación como fracción utilizando los valores de los lados correspondientes.
\(\cos A=\dfrac{38}{50}\)
A continuación, exprese la relación como decimal redondeado a cuatro lugares después del decimal.
\(\cos A=0.76\)
El decimal terminó. Podrías escribir el decimal como 0.7600 pero esto no es necesario.
A continuación, utilice la función coseno inversa (\(\cos^{−1}\)) en la calculadora TI para encontrar la medida de\(\angle A\).
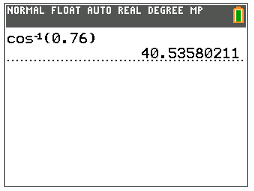
Después, escribe el valor de\(\angle A\) a la décima más cercana.
\(\angle A=40.5^{\circ}\)
La respuesta es\(40.5^{\circ}\)
Si\(\cos B=0.7984\), cuál es la medida de\(\angle B\) al décimo más cercano.
Solución
Primero, use la calculadora TI para determinar la medida de\(\angle B\) usando la función de coseno inverso (\ (\ cos^ {−1}) en la calculadora. Esta función está por encima del botón cos de la calculadora. Para acceder a esta función pulse
A continuación, ingrese el decimal 0.7984 entre paréntesis donde el cursor parpadea.
A continuación, presione enter y la pantalla de la calculadora mostrará la medida del ángulo.

Después, escribe la medida de\(\angle B\) a la décima más cercana.
\(\angle B=32.0^{\circ}\).
La respuesta es\(32.0^{\circ}\)
Para la siguiente solución que muestra usando la relación coseno para calcular la medida de\ ángulo B, dibujar y etiquetar el triángulo rectángulo ABC que se utilizó para hacer la solución.
\ (\ comenzar {alineado}
\ cos B &=\ frac {\ texto {adyacente}} {\ texto {hipotenusa}}
\\ cos B &=\ frac {B C} {A B}\
\ cos B &=\ frac {36} {76.7}\
\ cos B &=0.4694\
\ cos ^ {-1} (\ cos B) &=\ cos {^ -1} (0.4694)\\
\ ángulo B &=62.00454372\\
\ ángulo B &=62.0^ {\ circ}
\ final {alineado}\)
Solución
Primero, anote lo que sabes de la solución.
\(\Delta ABC\)es un triángulo rectángulo.
\(\overline{BC}\)es el lado adyacente del triángulo.
\(\overline{BC}\)tiene una longitud de 36.
\(\overline{AB}\)es la hipotenusa del triángulo.
\(\overline{AB}\)tiene una longitud de 76.7.
\(\angle B\)es el ángulo de referencia.
A continuación, usa la información que has escrito para dibujar y etiquetar el triángulo.
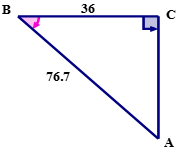
El triángulo anterior representa el problema.
Para el triángulo rectángulo dado, use la relación coseno para calcular la medida de\(\angle A\) al décimo más cercano.
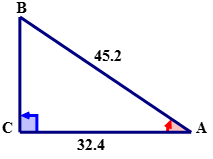
Solución
Primero, usando el ángulo de referencia nombra los lados del triángulo.
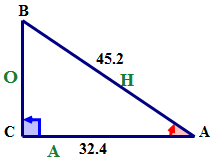
A continuación, escriba la relación coseno en palabras.
\(\cos A=\dfrac{\text{adjacent}}{\text{hypotenuse}}\)
A continuación, escribe la relación usando símbolos.
\(\cos A=\dfrac{AC}{AB}\)
A continuación, expresar la relación como fracción utilizando los valores de los lados correspondientes.
\(\cos A=\dfrac{32.4}{45.2}\)
A continuación, exprese la relación como decimal redondeado a cuatro lugares después del decimal.
\(\cos A=0.7168\)
A continuación, utilice la función coseno inversa (\(\cos^{−1}\)) en la calculadora TI para encontrar la medida de\(\angle A\).

Después, escribe la medida de\(\angle A\) a la décima más cercana.
\(\angle A=44.2^{\circ}\).
La respuesta es\(44.2^{\circ}\)
Revisar
Resolver cada problema.
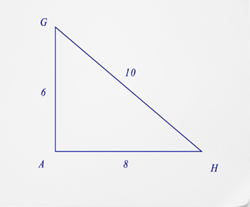
- ¿De qué es el coseno\(\angle G\)?
- ¿De qué es el coseno\(\angle H\)?
- ¿Cómo se identifica un coseno?
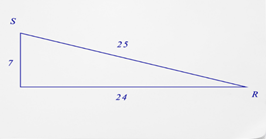
4. ¿De qué es el coseno\(\angle R\)?
5. ¿De qué es el coseno\(\angle S\)?
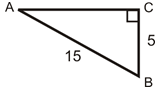
- ¿De qué es el coseno\(\angle A\)?
- ¿De qué es el coseno\(\angle B\)?
- ¿Cuál es la longitud del lado faltante redondeado a la centésima más cercana?
Responde a cada una de las siguientes preguntas.
- ¿El coseno está relacionado con un ángulo?
- ¿Necesitas conocer las longitudes laterales de un triángulo para escribir un coseno?
- ¿Qué longitudes laterales necesitas?
- Si el coseno fuera\(\dfrac{5}{20}\) ¿cuál sería el valor numérico del coseno?
- Si el coseno fuera\(\dfrac{5}{25}\) ¿cuál sería el valor numérico del coseno?
- Si el coseno fuera\(\dfrac{3}{33}\) ¿cuál sería el valor numérico del coseno?
- Si el coseno fuera\(\dfrac{12}{14}\) ¿cuál sería el valor numérico del coseno?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 7.14.
El vocabulario
| Término | Definición |
|---|---|
| coseno | El coseno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado adyacente al ángulo dado por la longitud de la hipotenusa. |
| Ratios trigonométricos | Relaciones que nos ayudan a entender las relaciones entre lados y ángulos de triángulos rectos. |

