2.5.1: Medida de radianes

Última actualización

30 oct 2022
Guardar como PDF
- 2.5: Radianes
- 2.5.2: Conversión entre Grados y Radianes

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

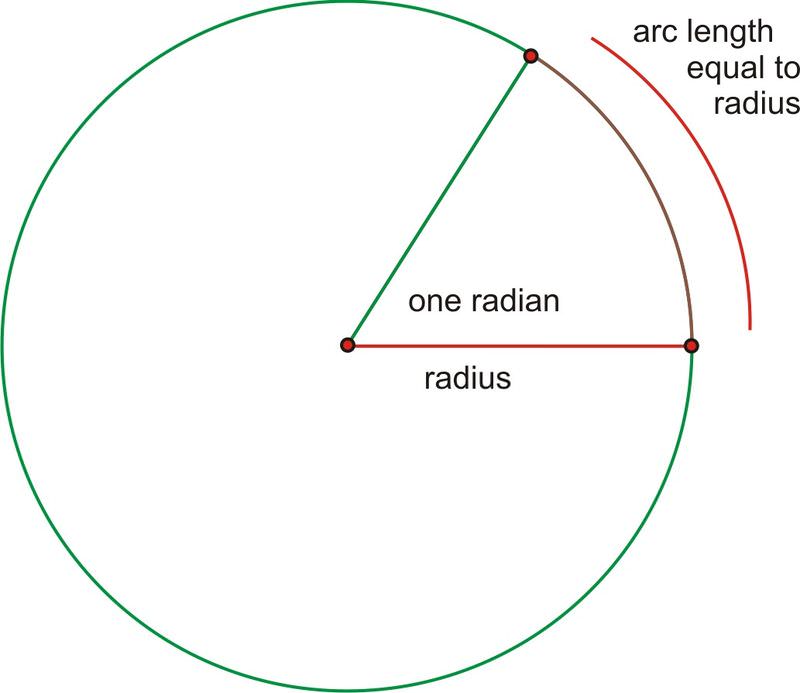
$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Medida del ángulo en un círculo donde la longitud del arco es igual al radio.

Mientras trabaja en un experimento en el laboratorio de ciencias de tu escuela, tu profesor te pide que enciendas un detector girando $\dfrac{\pi}{2}$ los radianes de la perilla. De inmediato te desconcierta, ya que no sabes qué es una medida de radianes o hasta qué punto girar la perilla.

Medida de Radianes

Hasta ahora, hemos utilizado grados para medir ángulos. Pero, ¿qué es exactamente un título? Un grado es $\dfrac{1}{360^{th}}$ de una rotación completa alrededor de un círculo. Los radianes son unidades alternas utilizadas para medir ángulos en trigonometría. Así como suena, un radián se basa en el radio de un círculo. Un radián (rad abreviado) es el ángulo creado al doblar la longitud del radio alrededor del arco de un círculo. Debido a que un radián se basa en una parte real del círculo más que en una división arbitraria, es una unidad de medida de ángulo mucho más natural para las matemáticas de nivel superior.

F-d_6532ed12785f09eb05555b2acc0f7292d795bf6d18f55fd5ec2e7f6e+image_tiny+image_tiny.jpg — Figura $\PageIndex{1}$

¿Y si giráramos todo el círculo? Continuando agregando longitudes de radio, encontramos que se necesitan un poco más de 6 de ellos para completar la rotación.

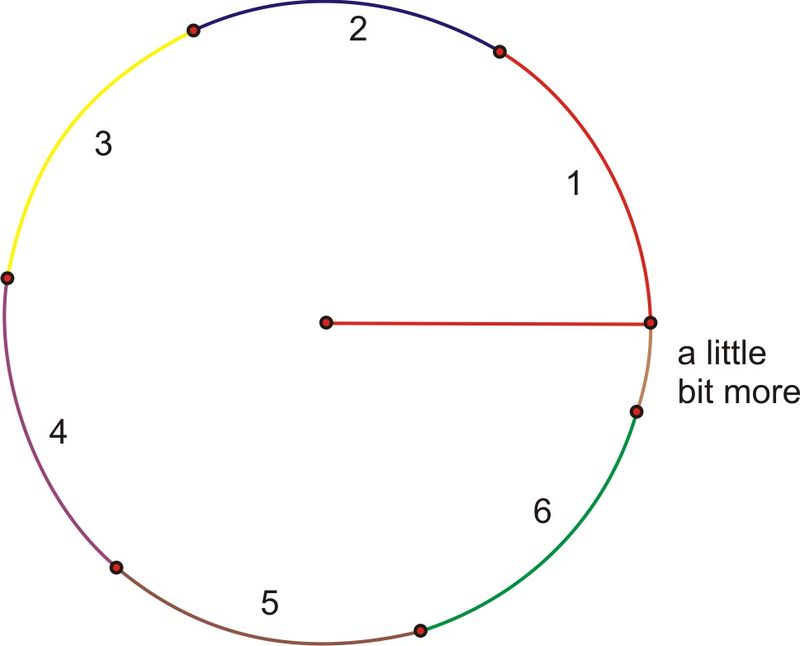
f-d_7a987c44dbcae900c736264aea753f083b1fd25bc9a53380d543dbbc+image_tiny+image_tiny.jpg — Figura $\PageIndex{2}$

Recordemos de la geometría que la longitud del arco de una rotación completa es la circunferencia, donde la fórmula es igual a $2\pi$ veces la longitud del radio. $2\pi$ es aproximadamente 6.28, por lo que la circunferencia es un poco más de 6 longitudes de radio. O, en términos de medida de radianes, una rotación completa (360 grados) son $2\pi$ radianes.

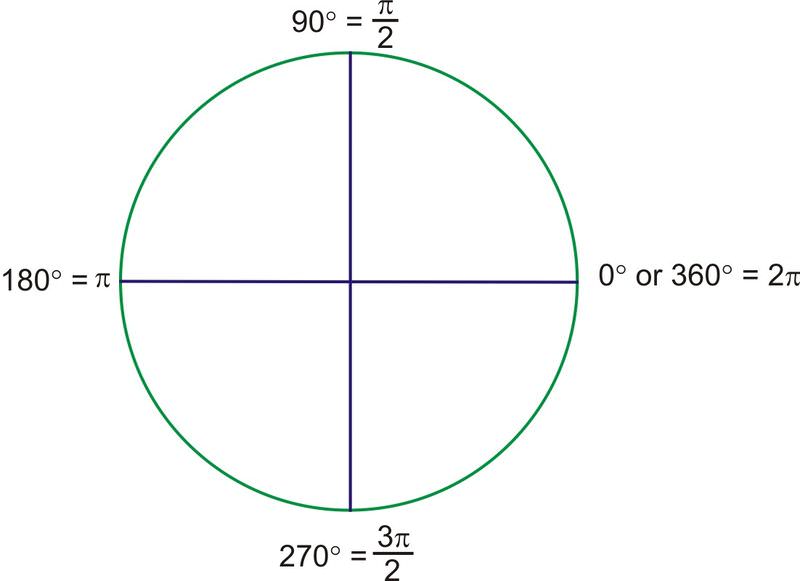
$360\text{ degrees}=2\pi \text{ radians}$

Con esto como nuestro punto de partida, podemos encontrar la medida radianes de otros ángulos. La mitad de una rotación, o 180 grados, debe ser por lo tanto $\pi$ radianes, y 90 grados deben ser $\dfrac{1}{2}\pi$ , escritos $\dfrac{\pi}{2}$ .

Extendiendo la medida del radián más allá del primer cuadrante, se han determinado los ángulos cuadránticos, excepto $270^{\circ}$ . Porque $270^{\circ}$ está a medio camino entre $180^{\circ}$ ( $\pi$ ) y $360^{\circ}$ ( $2\pi$ ), debe ser $1.5\pi$ , generalmente escrito $\dfrac{3\pi}{2}$ .

F-d_f855149c973f405591307fc63537c3530b896d9ff03c1b6a19ad28f1+image_tiny+image_tiny.jpg — Figura $\PageIndex{3}$

Para los $45^{\circ}$ ángulos, los radianes son todos múltiplos de $\dfrac{\pi}{4}$ .

Por ejemplo, $135^{\circ}$ es $3\cdot 45^{\circ}$ . Por lo tanto, la medida radianes debe ser $3\cdot \dfrac{\pi}{4}$ , o $\dfrac{3\pi}{4}$ . Aquí están el resto de los múltiplos de $45^{\circ}$ , en radianes:

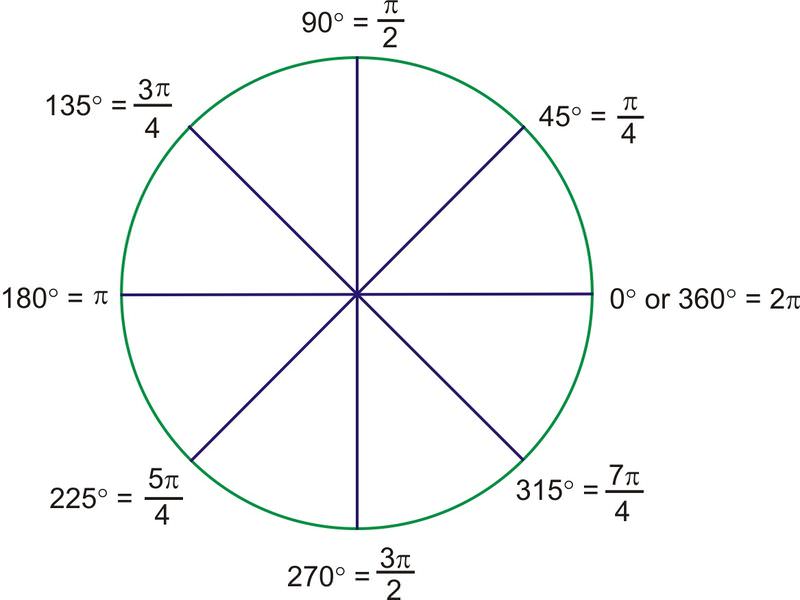
F-d_4dad0f91135a66c1c4d5af3b16f02b93914953d0a5852955ed807654+image_tiny+image_tiny.jpg — Figura $\PageIndex{4}$

Observe que los ángulos adicionales en el dibujo tienen todos ángulos de referencia de 45 grados y sus medidas de radianes son todos múltiplos de $\dfrac{\pi}{4}$ . Todos los múltiplos pares son los ángulos cuadránticos y se reducen, al igual que cualquier otra fracción.

Hagamos algunos problemas que involucren medidas radianes.

1. Encuentra la medida radianes de estos ángulos.

Ángulo en Grados	Ángulo en Radianes
90	$\dfrac{\pi}{2}$
45
30

Porque 45 es la mitad de 90, la mitad de $\dfrac{1}{2}\pi$ es $\dfrac{1}{4}\pi$ . 30 es un tercio de un ángulo recto, por lo que multiplicar da:

$\dfrac{\pi}{2}\times \dfrac{1}{3}=\dfrac{\pi}{6}$

y porque 60 es dos veces más grande que 30:

$2\times \dfrac{\pi}{6}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}$

Aquí está la tabla terminada:

Ángulo en Grados	Ángulo en Radianes
90	$\dfrac{\pi}{2}$
45	$\dfrac{\pi}{4}$
30	$\dfrac{\pi}{6}$

Existe una fórmula para convertir entre radianes y grados que quizás ya hayas descubierto al hacer este ejemplo. Sin embargo, muchos ángulos que se utilizan comúnmente se pueden encontrar fácilmente a partir de los valores de esta tabla. Por ejemplo, a la mayoría de los estudiantes les resulta fácil recordar 30 y 60. 30 es $\pi$ mayor de 6 y $\pi$ 60 es mayor de 3. Conociendo estos ángulos, puedes encontrar cualquiera de los ángulos especiales que tengan ángulos de referencia de 30 y 60 porque todos tendrán los mismos denominadores. Lo mismo ocurre con los múltiplos de $\dfrac{\pi}{4}$ (45 grados) y $\dfrac{\pi}{2}$ (90 grados).

2. Complete las siguientes medidas radianes contando en múltiplos de $\dfrac{\pi}{3}$ y $\dfrac{\pi}{6}$ :

F-d_09e4ee6264ae6ea93e8d666af32ebdf148fa3c94904c65cdc9dcbc5b+image_tiny+image_tiny.jpg — Figura $\PageIndex{5}$

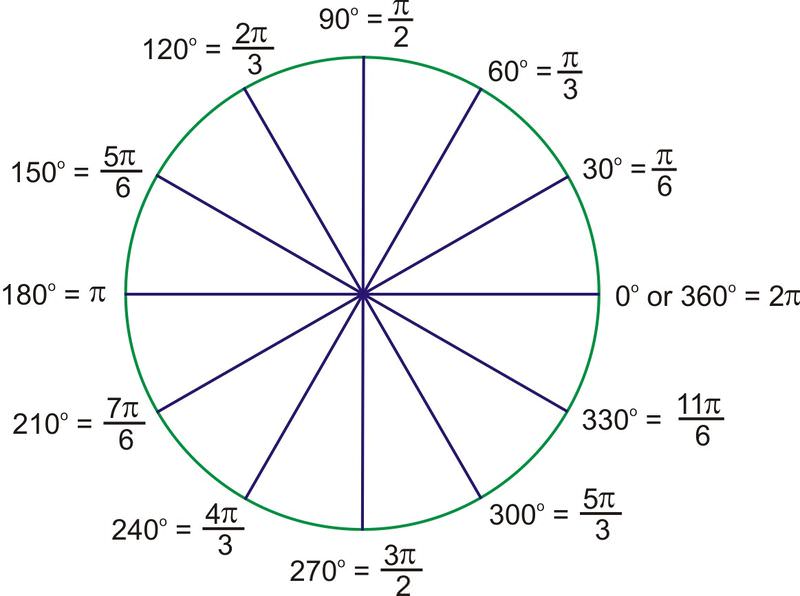
f-d_d216430ac319ba00de1731d8b2ece54642ee3d44456d7f8c85fe38+image_tiny+image_tiny+image_tiny.jpg — Figura $\PageIndex{6}$

Observe que todos los ángulos con ángulos de referencia de 60 grados son múltiplos de $\dfrac{\pi}{3}$ , y todos aquellos con ángulos de referencia de 30 grados son múltiplos de $\dfrac{\pi}{6}$ . Contar en estos términos con base en este patrón, en lugar de volver a convertir a grados, te ayudará a entender mejor los radianes.

3. Encuentra la medida radianes de estos ángulos.

Ángulo en Grados	Ángulo en Radianes
120	$\dfrac{2 \pi}{3}$
180
240
270
300

Debido a que 30 es un tercio de un ángulo recto, multiplicar da:

$\dfrac{\pi}{2}\times 13=\dfrac{\pi}{6}$

sumando esto al valor conocido para noventa grados de $\dfrac{\pi}{2}$ :

$\dfrac{\pi}{2}+\dfrac{\pi}{6}=3\dfrac{\pi}{6}+\dfrac{\pi}{6}=4\dfrac{\pi}{6}=\dfrac{2 \pi}{3}$

Aquí está la tabla terminada:

Ángulo en Grados	Ángulo en Radianes
120	$\dfrac{2\pi}{3}$
180	$\pi$
240	$\dfrac{4\pi}{3}$
300	$\dfrac{5\pi}{3}$

Ejemplo $\PageIndex{1}$

Antes, se le dio un problema de girar la perilla.

Solución

Desde $45^{\circ} =\dfrac{\pi}{4} \text{ rad}$ entonces $2\times \dfrac{\pi}{4}=\dfrac{\pi}{2}=2\times 45^{\circ}$ . Por lo tanto, un giro de $\dfrac{\pi}{2}$ es igual a $90^{\circ}$ , que es $\dfrac{1}{4}$ de una rotación completa de la perilla.

Ejemplo $\PageIndex{2}$

Dar la medida radianes de $60^{\circ}$

Solución

30 es un tercio de un ángulo recto. Esto quiere decir que desde $90^{\circ} =\dfrac{\pi}{2}$ , entonces $30^{\circ} =\dfrac{\pi}{6}$ . Por lo tanto, multiplicar da:

$\dfrac{\pi}{6}\times 2=\dfrac{\pi}{3}$

Ejemplo $\PageIndex{3}$

Dar la medida radianes de $75^{\circ}$

Solución

15 es una sexta parte de un triángulo rectángulo. Esto quiere decir que desde $90^{\circ} =\dfrac{\pi}{2}$ , entonces $15^{\circ} =\dfrac{\pi}{12}$ . Por lo tanto, multiplicar da:

$\dfrac{\pi}{12}\times 5=\dfrac{5\pi}{12}$

Ejemplo $\PageIndex{4}$

Dar la medida radianes de $180^{\circ}$

Solución

Desde $90^{\circ} =\dfrac{\pi}{2}$ entonces $180^{\circ} =\dfrac{2\pi}{2}=\pi$

Revisar

Encuentra la medida de radianes de cada ángulo.

$90^{\circ}$
$120^{\circ}$
$300^{\circ}$
$330^{\circ}$
$−45^{\circ}$
$135^{\circ}$

Encuentra la medida de grado de cada ángulo.

$\dfrac{3\pi}{2}$
$\dfrac{5\pi}{4}$
$\dfrac{7\pi}{6}$
$\dfrac{\pi}{6}$
$\dfrac{5\pi}{3}$
$\pi$
Explica por qué si te dan un ángulo en grados y lo $\dfrac{\pi}{180}$ multiplicas por obtendrás el mismo ángulo en radianes.
Explica por qué si te dan un ángulo en radianes y lo $\dfrac{180}{\pi}$ multiplicas por obtendrás el mismo ángulo en grados.
Explica con tus propias palabras por qué tiene sentido que haya $2\pi$ radianes en un círculo.

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.1.

El vocabulario

Término	Definición
radián	Un radián es una unidad de ángulo que es igual al ángulo creado en el centro de un círculo cuyo arco es igual en longitud al radio.

Recursos adicionales

Elemento interactivo

Video: Medidas de ángulo - Descripción general

Práctica: Medida de radianes

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo $\PageIndex{1}$

Ejemplo $\PageIndex{2}$

Ejemplo $\PageIndex{3}$

Ejemplo $\PageIndex{4}$

Elemento interactivo

Medida de Radianes

Ejemplo2.5.1.1\PageIndex{1}

Ejemplo2.5.1.2\PageIndex{2}

Ejemplo2.5.1.3\PageIndex{3}

Ejemplo2.5.1.4\PageIndex{4}

Revisar

Reseña (Respuestas)

El vocabulario

Recursos adicionales

Elemento interactivo

Support Center

How can we help?

Ejemplo $\PageIndex{1}$

Ejemplo $\PageIndex{2}$

Ejemplo $\PageIndex{3}$

Ejemplo $\PageIndex{4}$