5.2.3: Forma rectangular a polar para ecuaciones

Convierte ecuaciones sustituyendo x e y con expresiones de distancia y ángulos.

Estás trabajando diligentemente en tu clase de matemáticas cuando tu profesor te da una ecuación para graficar:

\((x+1)^2−(y+2)^2=7\)

A medida que comienzas a considerar cómo reorganizar esta ecuación, te dicen que el objetivo de la clase es convertir la ecuación a forma polar en lugar de forma rectangular.

¿Puedes encontrar la manera de hacer esto?

Ecuaciones rectangulares a la forma polar

Curiosamente, un sistema de coordenadas rectangulares no es la única forma de trazar valores. Un sistema polar puede ser útil. Sin embargo, a menudo ocurrirá que hay una o más ecuaciones que necesitan ser convertidas de forma rectangular a polar. Para escribir una ecuación rectangular en forma polar, se\(y=r\sin \theta\) utilizan las ecuaciones de conversión de\(x=r\cos \theta\) y.

Si la gráfica de la ecuación polar es la misma que la gráfica de la ecuación rectangular, entonces la conversión se ha determinado correctamente.

Figura\(\PageIndex{1}\)

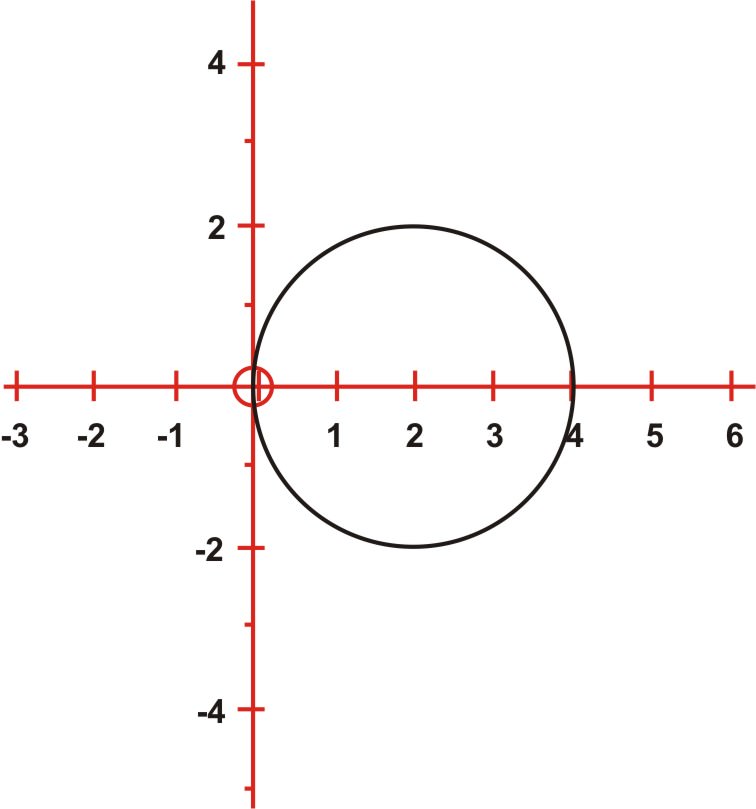
\((x−2)^2+y^2=4\)

Figura\(\PageIndex{2}\)

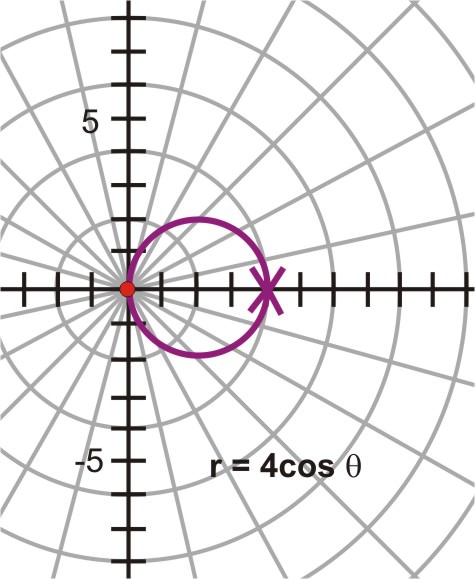
La ecuación rectangular\((x−2)^2+y^2=4\) representa un círculo con centro\((2, 0)\) y un radio de 2 unidades. La ecuación polar\(r=4\cos \theta\) es un círculo con centro\((2, 0)\) y un radio de 2 unidades.

Conversión de ecuaciones

1. Escribe la ecuación rectangular\(x^2+y^2=2x\) en forma polar.

Recuerda\(r=\sqrt{x^2+y^2}\),\(r^2=x^2+y^2\) y\(x=r\cos \theta\).

\(\begin{aligned} x^2+y^2 &=2x\\ r^2 &=2(r\cos \theta) &&\text{Pythagorean Theorem }\\ r^2 &=2r\cos \theta\\ r&=2\cos \theta and x=r\cos \theta && \text{Divide each side by r}\end{aligned}\)

2. Escribir\((x−2)^2+y^2=4\) en forma polar.

Recuerda\(x=r\cos \theta\) y\(y=r\sin \theta\).

\ (\ begin {alineado} (x-2) ^ {2} +y^ {2} &=4\\ (r\ cos\ theta-2) ^ {2} + (r\ sin\ theta) ^ {2} &=4 && x=r\ cos\ theta\ text {y} y=r\ sin\ theta\ r^ {2}\ cos ^ {2}\ theta eta-4 r\ cos\ theta+4+r^ {2}\ sin ^ {2}\ theta&=4 &&\ text {expandir los términos}\\ r^ {2}\ cos ^ {2}\ theta-4 r\ cos\ theta+r^ {2}\ sin ^ { 2}\ theta&=0 &&\ text {restar 4 de cada lado}\\ r^ {2}\ cos ^ {2}\ theta+r^ {2}\ sin ^ {2}\ theta&=4 r\ cos\ theta &&\ text {aislar los términos cuadrados}\\ r^ {2}\ left (\ cos ^ {2}\ theta+\ sin ^ {2}\ theta\ derecha) &=4 r\ cos\ theta &&\ texto {factor} r^ {2}\ texto {-a factor común}\\
r^ {2} &=4 r\ cos\ theta &&\ text {Identidad pitagórica}\\ r&=4\ cos\ theta &&\ text {Divide cada lado por} r\ end {alineado}\)

3. Escribe la ecuación rectangular\((x+4)^2+(y−1)^2=17\) en forma polar.

\(\begin{aligned} (x+4)^{2}+(y-1)^{2}&=17 \\ (r \cos \theta+4)^{2}+(r \sin \theta-1)^{2}&=17 && x=r \cos \theta \text{ and } y=r \sin \theta \\ r^{2} \cos ^{2} \theta+8 r \cos \theta+16+r^{2} \sin ^{2} \theta-2 r \sin \theta+1&=17 && \text{ expand the terms} \\ r^{2} \cos ^{2} \theta+8 r \cos \theta-2 r \sin \theta+r^{2} \sin ^{2} \theta&=0 && \text{ subtract 17 from each side} \\ r^{2} \cos ^{2} \theta+r^{2} \sin ^{2} \theta&=-8 r \cos \theta+2 r \sin \theta && \text{isolate the squared terms} \\ r^{2}\left(\cos ^{2} \theta+\sin ^{2} \theta\right)&=-2 r(4 \cos \theta-\sin \theta) && \text{ factor } r^{2} \text{-a common factor} \\ r^{2}&=-2 r(4 \cos \theta-\sin \theta) && \text{ Pythagorean Identity} \\ r&=-2(4 \cos \theta-\sin \theta) && \text{ Divide each side by } r \end{aligned}\)

Ejemplo\(\PageIndex{1}\)

Anteriormente, se le pidió convertir una ecuación a forma polar.

Solución

La ecuación original a convertir es:

\((x+1)^2−(y+2)^2=7\)

Se puede sustituir\(x=r\cos \theta\) y\(y=r\sin \theta\) en la ecuación, y luego simplificar:

\ (\ comenzar {alineado}
(r\ cos\ theta+1) ^ {2} - (r\ sin\ theta+2) ^ {2} &=7\\
\ izquierda (r^ {2}\ cos ^ {2}\ theta+2 r\ cos\ theta+1\ derecha) -\ izquierda (r^ {2}\ sin ^ {2}\ theta+4 r\ sin\ theta+4\ derecha) &=7\\
r^ {2}\ izquierda (\ cos ^ {2}\ theta-\ sin ^ {2}\ theta\ derecha) +2 r (\ cos\ theta-2\ sin\ theta) -3&=7\\
r^ {2}\ izquierda (\ cos ^ {2}\ theta-\ sin ^ {2}\ theta\ derecha) +2 r (\ cos\ theta-2\ sin\ theta) &=10
\ end {alineado}\)

Ejemplo\(\PageIndex{2}\)

Escribe la ecuación rectangular\((x−4)^2+(y−3)^2=25\) en forma polar.

Solución

\ (\ begin {alineado}
(x-4) ^ {2} + (y-3) ^ {2} &=25\\
x^ {2} -8 x+16+y^ {2} -6 y+9 &=25\\
x^ {2} -8 x+y^ {2} -6 y+25 &=25\\
x^ {2} -8 x+y^ {2} -6 y &=0\\
x^ {2} +y^ {2} -8 x-6 y &=0\\
r^ {2} -8 (r\ cos\ theta) -6 (r\ sin\ theta) &=0\\
r^ {2} -8 r\ cos\ theta-6 r\ sin\ theta &=0\\
r (r-8\ cos\ theta-6\ sin\ theta) &=0\
r=0\ texto {o} r-8\ cos\ theta-6\ sin\ theta &=0\
r=0\ texto {o} r &=8 cos\ theta+6\ sin\ theta
\ fin {alineado}\)

Al graficar r−8\ cos\ theta−6\ sin\ theta=0, vemos que las soluciones adicionales son 0 y 8.

Ejemplo\(\PageIndex{3}\)

Escribe la ecuación rectangular\(3x−2y=1\) en forma polar.

Solución

\(\begin{aligned} 3x−2y&=1 \\ 3r\cos \theta−2r\sin \theta &=1\\ r(3\cos \theta−2\sin \theta) &=1\\ r&=\dfrac{1}{3\cos \theta−2\sin \theta} \end{aligned}\)

Ejemplo\(\PageIndex{4}\)

Escribe la ecuación rectangular\(x^2+y^2−4x+2y=0\) en forma polar.

Solución

\ (\ begin {alineado}
x^ {2} +y^ {2} -4 x+2 y &=0\\
r^ {2}\ cos ^ {2}\ theta+r^ {2}\ sin ^ {2}\ theta-4 r\ cos\ theta+2 r\ sin\ theta &=0\\
r^ {2}\ izquierda (\ sin ^ {2}\ theta+2 r\ sin\ theta a+\ cos ^ {2}\ theta\ derecha) -4 r\ cos\ theta+2 r\ sin\ theta &=0\\
r (r-4\ cos\ theta+2\ sin\ theta) &=0\\
r=0\ texto {o} r-4\ cos\ theta+2\ sin\ theta &=0\\
r=0\ texto {o} r &=4\ cos\ theta-2\ sin\ theta
\ end {alineado}\)

Revisar

Escribe cada ecuación rectangular en forma polar.

1. \(x=3\)
2. \(y=4\)
3. \(x^2+y^2=4\)
4. \(x^2+y^2=9\)
5. \((x−1)^2+y^2=1\)
6. \((x−2)^2+(y−3)^2=13\)
7. \((x−1)^2+(y−3)^2=10\)
8. \((x+2)^2+(y+2)^2=8\)
9. \((x+5)^2+(y−1)^2=26\)
10. \(x^2+(y−6)^2=36\)
11. \(x^2+(y+2)^2=4\)
12. \(2x+5y=11\)
13. \(4x−7y=10\)
14. \(x+5y=8\)
15. \(3x−4y=15\)

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.6.

Recursos adicionales

Video: Ejemplo: Encontrar la ecuación polar para una línea

Práctica: Forma rectangular a polar para ecuaciones