5.7: Distribución binomial
- Page ID
- 152439
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Definir resultados binomiales
- Calcular la probabilidad de obtener\(X\) éxitos en los\(N\) ensayos
- Computar probabilidades binomiales acumuladas
- Encontrar la media y desviación estándar de una distribución binomial
Al lanzar una moneda, hay dos posibles resultados: cabeza y cola. Cada resultado tiene una probabilidad fija, la misma de un juicio a otro. En el caso de las monedas, las cabezas y las colas tienen cada una la misma probabilidad de\(1/2\). De manera más general, hay situaciones en las que la moneda está sesgada, de manera que la cabeza y la cola tienen diferentes probabilidades. En la presente sección, consideramos distribuciones de probabilidad para las cuales solo hay dos posibles resultados con probabilidades fijas sumando a uno. Estas distribuciones se denominan distribuciones binomiales.
Un ejemplo sencillo
Los cuatro posibles resultados que podrían ocurrir si volteó una moneda dos veces se enumeran a continuación en la Tabla\(\PageIndex{1}\). Tenga en cuenta que los cuatro resultados son igualmente probables: cada uno tiene probabilidad\(1/4\). Para ver esto, tenga en cuenta que los tirados de la moneda son independientes (ninguno afecta al otro). De ahí que la probabilidad de una cabeza\(\text{Flip 1}\) y una cabeza en\(\text{Flip 2}\) es producto de\(P(H)\) y\(P(H)\), que es\(1/2 \times 1/2 = 1/4\). El mismo cálculo se aplica a la probabilidad de una cabeza\(\text{Flip 1}\) y una cola en\(\text{Flip 2}\). Cada uno es\(1/2 \times 1/2 = 1/4\).
| Resultado | Primer volteo | Segundo volteo |
|---|---|---|
| 1 | Cabezales | Cabezales |
| 2 | Cabezales | Tails |
| 3 | Tails | Cabezales |
| 4 | Tails | Tails |
Los cuatro posibles resultados se pueden clasificar en cuanto al número de cabezas que surja. El número podría ser dos (Resultado\(1\), uno (Resultados\(2\) y\(3\)) o\(0\) (Resultado\(4\)). Las probabilidades de estas posibilidades se muestran en la Tabla\(\PageIndex{2}\) y en la Figura\(\PageIndex{1}\).
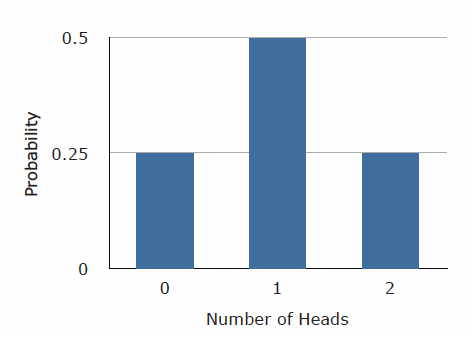
Dado que dos de los resultados representan el caso en el que solo aparece una cabeza en los dos tiradas, la probabilidad de este evento es igual a\(1/4 + 1/4 = 1/2\). Cuadro\(\PageIndex{2}\) resume la situación.
| Número de cabezales | Probabilidad |
|---|---|
| 0 | 1/4 |
| 1 | 1/2 |
| 2 | 1/4 |
La figura\(\PageIndex{1}\) es una distribución de probabilidad discreta: Muestra la probabilidad para cada uno de los valores en el\(X\) eje -eje. Definir una cabeza como un “éxito”, la Figura\(\PageIndex{1}\) muestra la probabilidad de\(0\)\(1\), y\(2\) éxitos para dos ensayos (volteretas) para un evento que tiene una probabilidad\(0.5\) de ser un éxito en cada ensayo. Esto hace de Figura\(\PageIndex{1}\) un ejemplo de una distribución binomial.
La fórmula para las probabilidades binomiales
La distribución binomial consiste en las probabilidades de cada uno de los posibles números de éxitos en\(N\) ensayos para eventos independientes que cada uno tiene una probabilidad de ocurrir\(\pi\) (la letra griega pi). Para el ejemplo de flip de monedas,\(N = 2\) y\(\pi =0.5\). La fórmula para la distribución binomial se muestra a continuación:
\[P(x)=\dfrac{N!}{x!(N-x)!}\pi ^x(1-\pi )^{N-x}\]
donde\(P(x)\) está la probabilidad de x éxitos fuera de\(N\) los ensayos,\(N\) es el número de ensayos, y\(\pi\) es la probabilidad de éxito en un ensayo dado. Aplicando esto al ejemplo de flip de monedas,
\[\begin{align} P(0)&=\dfrac{2!}{0!(2-0)!}(0.5)^0(1-0.5)^{2-0} \\[5pt] &=\dfrac{2}{2}(1)(0.25) \\[5pt] &=0.25 \end{align}\]
\[\begin{align}P(0)&=\dfrac{2!}{1!(2-1)!}(0.5)^1(1-0.5)^{2-1} \\[5pt] &=\dfrac{2}{1}(0.5)(0.5) \\[5pt] &=0.50\end{align}\]
\[\begin{align}P(0)&=\dfrac{2!}{2!(2-2)!}(0.5)^2(1-0.5)^{2-2} \\[5pt] &=\dfrac{2}{2}(0.25)(1) \\[5pt] &=0.25\end{align}\]
Si volteas una moneda dos veces, ¿cuál es la probabilidad de obtener una o más cabezas? Dado que la probabilidad de obtener exactamente una cabeza es\(0.50\) y la probabilidad de obtener exactamente dos cabezas es\(0.25\), la probabilidad de obtener una o más cabezas es\(0.50 + 0.25 = 0.75\).
Ahora supongamos que la moneda está sesgada. La probabilidad de cabezas es sólo\(0.4\). ¿Cuál es la probabilidad de conseguir cabezas al menos una vez en dos tiradas? Sustituyendo a la fórmula general anterior, debes obtener la respuesta\(0.64\).
Probabilidades acumuladas
Echamos una moneda\(12\) veces. ¿Cuál es la probabilidad de que lleguemos de\(0\) a\(3\) cabezas? La respuesta se encuentra calculando la probabilidad de exactamente\(0\) cabezas, exactamente\(1\) cabeza, exactamente\(2\) cabezas y exactamente\(3\) cabezas. La probabilidad de llegar de\(0\) a\(3\) cabezas es entonces la suma de estas probabilidades. Las probabilidades son:\(0.0002\),\(0.0029\),\(0.0161\), y\(0.0537\). La suma de las probabilidades es\(0.073\). El cálculo de las probabilidades binomiales acumuladas puede ser bastante tedioso. Por lo tanto, hemos proporcionado una calculadora binomial para facilitar el cálculo de estas probabilidades.
Media y Desviación Estándar de Distribuciones Binomiales
Considera un experimento de lanzamiento de monedas en el que arrojaste una moneda\(12\) veces y registraste el número de cabezas. Si realizaras este experimento una y otra vez, ¿cuál sería el número medio de cabezas? En promedio, se esperaría que la mitad de los tirados de monedas salieran de cabeza. Por lo tanto el número medio de cabezas sería\(6\). En general, la media de una distribución binomial con parámetros\(N\) (el número de ensayos) y\(\pi\) (la probabilidad de éxito en cada ensayo) es:
\[\mu =N\pi\]
donde\(\mu\) es la media de la distribución binomial. La varianza de la distribución binomial es:
\[\sigma ^2=N\pi (1-\pi )\]
donde\(\sigma ^2\) es la varianza de la distribución binomial.
Volvamos al experimento de arrojar monedas. La moneda fue tirada\(12\) veces, entonces\(N = 12\). Una moneda tiene probabilidad\(0.5\) de subir cabezas. Por lo tanto,\(\pi =0.5\). Por lo tanto, la media y varianza se pueden calcular de la siguiente manera:
\[\mu =N\pi =(12)(0.5)=6\]
\[\sigma ^2=N\pi (1-\pi )=(12)(0.5)(1.0-0.5)=3.0\]
Naturalmente, la desviación estándar (\(\sigma\)) es la raíz cuadrada de la varianza (\(\sigma ^2\)).
\[\sigma =\sqrt{N\pi (1-\pi )}\]


