6.2: La distribución normal estándar
- Page ID
- 153308
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Puntajes Z
La distribución normal estándar es una distribución normal de valores estandarizados llamada z-scores. Se mide una puntuación z en unidades de la desviación estándar.
Definición: Z-Score
Si\(X\) es una variable aleatoria normalmente distribuida y\(X \sim N(\mu, \sigma)\), entonces la puntuación z es:
\[z = \dfrac{x - \mu}{\sigma} \label{zscore}\]
La puntuación z te indica cuántas desviaciones estándar\(x\) está el valor por encima (a la derecha de) o por debajo (a la izquierda de) la media,\(\mu\). Los valores de\(x\) eso son mayores que la media tienen\(z\) puntuaciones positivas, y los valores de\(x\) que son menores que la media tienen\(z\) puntuaciones negativas. Si\(x\) es igual a la media, entonces\(x\) tiene un\(z\) -score de cero. Por ejemplo, si la media de una distribución normal es cinco y la desviación estándar es dos, el valor 11 es tres desviaciones estándar por encima (o a la derecha de) la media. El cálculo es el siguiente:
\[ \begin{align*} x &= \mu + (z)(\sigma) \\[5pt] &= 5 + (3)(2) = 11 \end{align*}\]
La puntuación z es de tres.
Dado que la media para la distribución normal estándar es cero y la desviación estándar es uno, entonces la transformación en Ecuación\ ref {zscore} produce la distribución\(Z \sim N(0, 1)\). El valor\(x\) proviene de una distribución normal con media\(\mu\) y desviación estándar\(\sigma\).
Se mide una puntuación z en unidades de la desviación estándar.
Ejemplo\(\PageIndex{1}\)
Supongamos\(X \sim N(5, 6)\). Esto dice que\(x\) es una variable aleatoria normalmente distribuida con media\(\mu = 5\) y desviación estándar\(\sigma = 6\). Supongamos\(x = 17\). Luego (vía Ecuación\ ref {zscore}):
\[z = \dfrac{x-\mu}{\sigma} = \dfrac{17-5}{6} = 2 \nonumber\]
Esto significa que\(x = 17\) se encuentran dos desviaciones estándar (2\(\sigma\)) por encima o a la derecha de la media\(\mu = 5\). La desviación estándar es\(\sigma = 6\).
Observe que:\(5 + (2)(6) = 17\) (El patrón es\(\mu + z \sigma = x\))
Ahora supongamos\(x = 1\). Entonces:
\[z = \dfrac{x-\mu}{\sigma} = \dfrac{1-5}{6} = -0.67 \nonumber\]
(redondeado a dos decimales)
Esto significa que\(x = 1\) se encuentran las desviaciones\(0.67\) estándar (\(–0.67\sigma\)) por debajo o a la izquierda de la media\(\mu = 5\). Observe que:\(5 + (–0.67)(6)\) es aproximadamente igual a uno (Esto tiene el patrón\(\mu + (–0.67)\sigma = 1\))
Resumiendo, cuando\(z\) es positivo,\(x\) está arriba o a la derecha de\(\mu\) y cuando\(z\) es negativo,\(x\) está a la izquierda o abajo\(\mu\). O, cuando\(z\) es positivo,\(x\) es mayor que\(\mu\), y cuando\(z\) es negativo\(x\) es menor que\(\mu\).
Ejercicio\(\PageIndex{1}\)
¿Cuál es la\(z\) puntuación de\(x\), cuándo\(x = 1\) y\(X \sim N(12, 3)\)?
- Contestar
-
\(z = \dfrac{1-12}{3} \approx -3.67\)
Ejemplo\(\PageIndex{2}\)
Algunos médicos creen que una persona puede perder cinco libras, en promedio, en un mes al reducir su ingesta de grasa y al hacer ejercicio consistentemente. Supongamos que la pérdida de peso tiene una distribución normal. Dejar\(X =\) la cantidad de peso perdido (en libras) por una persona en un mes. Use una desviación estándar de dos libras. \(X \sim N(5, 2)\). Rellene los espacios en blanco.
- Supongamos que una persona perdió diez libras en un mes. El\(z\) puntaje -cuando\(x = 10\) libras es\(x = 2.5\) (verificar). Esta\(z\) -puntuación te dice que\(x = 10\) es ________ desviaciones estándar a la ________ (derecha o izquierda) de la media _____ (¿Cuál es la media?).
- Supongamos que una persona ganó tres libras (una pérdida de peso negativa). Después\(z =\) __________. Esta\(z\) -score te dice que\(x = -3\) es ________ desviaciones estándar a la __________ (derecha o izquierda) de la media.
RESPUESTAS
a. Esta\(z\) puntuación te dice que\(x = 10\) es 2.5 desviaciones estándar a la derecha de la media cinco.
b. Supongamos que las variables aleatorias\(X\) y\(Y\) tienen las siguientes distribuciones normales:\(X \sim N(5, 6)\) y\(Y \sim N(2, 1)\). Si\(x = 17\), entonces\(z = 2\). (Esto se mostró anteriormente.) Si\(y = 4\), ¿qué es\(z\)?
\[z = \dfrac{y-\mu}{\sigma} = \dfrac{4-2}{1} = 2 \nonumber\]
dónde\(\mu = 2\) y\(\sigma = 1\).
El\(z\) -score para\(y = 4\) es\(z = 2\). Esto significa que cuatro son desviaciones\(z = 2\) estándar a la derecha de la media. Por lo tanto,\(x = 17\) y\(y = 4\) son ambas dos (propias) desviaciones estándar a la derecha de sus respectivas medias.
El puntaje z nos permite comparar datos que se escalan de manera diferente. Para entender el concepto, supongamos\(X \sim N(5, 6)\) representa aumentos de peso para un grupo de personas que están tratando de aumentar de peso en un periodo de seis semanas y\(Y \sim N(2, 1)\) mide el mismo aumento de peso para un segundo grupo de personas. Un aumento de peso negativo sería una pérdida de peso. Dado que\(x = 17\) y\(y = 4\) son cada una dos desviaciones estándar a la derecha de sus medias, representan la misma ganancia de peso estandarizada en relación con sus medias.
Ejercicio\(\PageIndex{2}\)
Rellene los espacios en blanco.
Jerome promedia 16 puntos por juego con una desviación estándar de cuatro puntos. \(X \sim N(16, 4)\). Supongamos que Jerome anota diez puntos en un juego. El\(z\) —score cuando\(x = 10\) es\(-1.5\). Esta puntuación te dice que\(x = 10\) es _____ desviaciones estándar a la ______ (derecha o izquierda) de la media______ (¿Cuál es la media?).
- Contestar
-
1.5, izquierda, 16
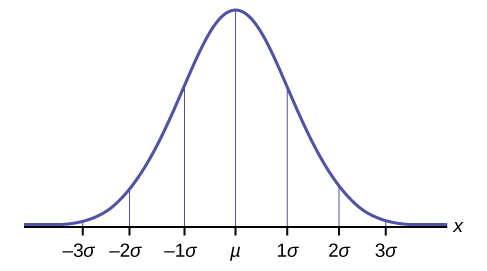
La regla empírica
Si\(X\) es una variable aleatoria y tiene una distribución normal con media\(\mu\) y desviación estándar\(\sigma\), entonces la Regla Empírica dice lo siguiente:
- Alrededor del 68% de los\(x\) valores se encuentran entre —1\(\sigma\) y +1\(\sigma\) de la media\(\mu\) (dentro de una desviación estándar de la media).
- Alrededor del 95% de los\(x\) valores se encuentran entre —2\(\sigma\) y +2\(\sigma\) de la media\(\mu\) (dentro de dos desviaciones estándar de la media).
- Alrededor del 99.7% de los\(x\) valores se encuentran entre —3\(\sigma\) y +3\(\sigma\) de la media\(\mu\) (dentro de tres desviaciones estándar de la media). Observe que casi todos los\(x\) valores se encuentran dentro de tres desviaciones estándar de la media.
- Las\(z\) puntuaciones -para +1\(\sigma\) y —1\(\sigma\) son +1 y —1, respectivamente.
- Las\(z\) puntuaciones -para +2\(\sigma\) y —2\(\sigma\) son +2 y —2, respectivamente.
- Las\(z\) puntuaciones -para +3\(\sigma\) y —3\(\sigma\) son +3 y —3 respectivamente.
La regla empírica también se conoce como la regla 68-95-99.7.
Ejemplo\(\PageIndex{3}\)
La estatura media de los varones de 15 a 18 años de Chile de 2009 a 2010 fue de 170 cm con una desviación estándar de 6.28 cm. Se sabe que las alturas masculinas siguen una distribución normal. Dejar\(X =\) la estatura de un varón de 15 a 18 años de Chile en 2009 a 2010. Entonces\(X \sim N(170, 6.28)\).
- Supongamos que un varón de 15 a 18 años de Chile metió 168 cm de altura entre 2009 y 2010. La\(z\) puntuación -cuando\(x = 168\) cm es\(z =\) _______. Esta\(z\) -puntuación te dice que\(x = 168\) es ________ desviaciones estándar a la ________ (derecha o izquierda) de la media _____ (¿Cuál es la media?).
- Supongamos que la estatura de un varón de 15 a 18 años de Chile de 2009 a 2010 tiene una\(z\) -score de\(z = 1.27\). ¿Cuál es la estatura del macho? El\(z\) -score (\(z = 1.27\)) te dice que la estatura del macho es ________ desviaciones estándar a la __________ (derecha o izquierda) de la media.
RESPUESTAS
- —0.32, 0.32, izquierda, 170
- 177.98, 1.27, derecha
Ejercicio\(\PageIndex{3}\)
Utilice la información de Ejemplo\(\PageIndex{3}\) para responder a las siguientes preguntas.
- Supongamos que un varón de 15 a 18 años de Chile metió 176 cm de altura entre 2009 y 2010. La\(z\) puntuación -cuando\(x = 176\) cm es\(z =\) _______. Esta\(z\) -puntuación te dice que\(x = 176\) cm es ________ desviaciones estándar a la ________ (derecha o izquierda) de la media _____ (¿Cuál es la media?).
- Supongamos que la estatura de un varón de 15 a 18 años de Chile de 2009 a 2010 tiene una\(z\) -score de\(z = –2\). ¿Cuál es la estatura del macho? El\(z\) -score (\(z = –2\)) te dice que la estatura del macho es ________ desviaciones estándar a la __________ (derecha o izquierda) de la media.
- Contestar
-
Resuelve la ecuación\(z = \dfrac{x-\mu}{\sigma}\) para\(z\). \(x = \mu+ (z)(\sigma)\)
\(z = \dfrac{176-170}{6.28}\), Esta puntuación z te dice que\(x = 176\) cm es 0.96 desviaciones estándar a la derecha de la media 170 cm.
- Contestar
-
Resuelve la ecuación\(z = \dfrac{x-\mu}{\sigma}\) para\(z\). \(x = \mu+ (z)(\sigma)\)
\(X = 157.44\)cm, El\(z\) -score (\(z = –2\)) te dice que la estatura del macho es de dos desviaciones estándar a la izquierda de la media.
Ejemplo\(\PageIndex{4}\)
De 1984 a 1985, la estatura media de los varones de 15 a 18 años de Chile fue de 172.36 cm y la desviación estándar fue de 6.34 cm. Dejar\(Y =\) la estatura de varones de 15 a 18 años de edad de 1984 a 1985. Entonces\(Y \sim N(172.36, 6.34)\).
La estatura media de los varones de 15 a 18 años de Chile de 2009 a 2010 fue de 170 cm con una desviación estándar de 6.28 cm. Se sabe que las alturas masculinas siguen una distribución normal. Dejar\(X =\) la estatura de un varón de 15 a 18 años de Chile en 2009 a 2010. Entonces\(X \sim N(170, 6.28)\).
Encuentra las puntuaciones z para\(x = 160.58\) cm y\(y = 162.85\) cm. Interpretar cada\(z\) partitura. ¿Qué puedes decir sobre\(x = 160.58\) cm y\(y = 162.85\) cm?
Contestar
- El\(z\) -score (Ecuación\ ref {zscore}) para\(x = 160.58\) es\(z = –1.5\).
- El\(z\) -score para\(y = 162.85\) es\(z = –1.5\).
Ambos\(x = 160.58\) y\(y = 162.85\) desvían el mismo número de desviaciones estándar de sus respectivas medias y en la misma dirección.
Ejercicio\(\PageIndex{4}\)
En 2012, 1,664,479 alumnos tomaron el examen SAT. La distribución de las puntuaciones en la sección verbal del SAT tuvo una media\(\mu = 496\) y una desviación estándar\(\sigma = 114\). Dejar\(X =\) una calificación de sección verbal del examen SAT en 2012. Entonces\(X \sim N(496, 114)\).
Encuentra los\(z\) puntajes para\(x_{1} = 325\) y\(x_{2} = 366.21\). Interpretar cada\(z\) partitura. ¿Qué puedes decir sobre\(x_{1} = 325\) y\(x_{2} = 366.21\)?
- Contestar
-
La puntuación z (Ecuación\ ref {zscore}) para\(x_{1} = 325\) es\(z_{1} = –1.15\).
La puntuación z (Ecuación\ ref {zscore}) para\(x_{2} = 366.21\) es\(z_{2} = –1.14\).
Estudiante 2 anotó más cerca de la media que el Estudiante 1 y, como ambos tuvieron\(z\) puntuaciones negativas, el Estudiante 2 tuvo la mejor puntuación.
Ejemplo\(\PageIndex{5}\)
Supongamos que x tiene una distribución normal con media 50 y desviación estándar 6.
- Alrededor del 68% de los valores x se encuentran dentro de una desviación estándar de la media. Por lo tanto, alrededor del 68% de los valores x se encuentran entre —1σ = (—1) (6) = —6 y 1σ = (1) (6) = 6 de la media 50. Los valores 50 — 6 = 44 y 50 + 6 = 56 están dentro de una desviación estándar de la media 50. Las puntuaciones z son —1 y +1 para 44 y 56, respectivamente.
- Alrededor del 95% de los valores x se encuentran dentro de dos desviaciones estándar de la media. Por lo tanto, alrededor del 95% de los valores de x se encuentran entre —2σ = (—2) (6) = —12 y 2σ = (2) (6) = 12. Los valores 50 — 12 = 38 y 50 + 12 = 62 están dentro de dos desviaciones estándar de la media 50. Las puntuaciones z son —2 y +2 para 38 y 62, respectivamente.
- Alrededor del 99.7% de los valores x se encuentran dentro de tres desviaciones estándar de la media. Por lo tanto, alrededor del 99.7% de los valores x se encuentran entre —3σ = (—3) (6) = —18 y 3σ = (3) (6) = 18 de la media 50. Los valores 50 — 18 = 32 y 50 + 18 = 68 están dentro de tres desviaciones estándar de la media 50. Las puntuaciones z son —3 y +3 para 32 y 68, respectivamente.
Ejercicio\(\PageIndex{5}\)
Supongamos que\(X\) tiene una distribución normal con media 25 y desviación estándar cinco. ¿Entre qué valores de\(x\) hacer el 68% de los valores se encuentran?
- Contestar
-
entre 20 y 30.
Ejemplo\(\PageIndex{6}\)
De 1984 a 1985, la estatura media de los varones de 15 a 18 años de Chile fue de 172.36 cm y la desviación estándar fue de 6.34 cm. Dejar\(Y =\) la altura de los varones de 15 a 18 años de edad en 1984 a 1985. Entonces\(Y \sim N(172.36, 6.34)\).
- ¿Alrededor del 68% de los\(y\) valores se encuentran entre qué dos valores? Estos valores son ________________. Los\(z\) puntajes -son ________________, respectivamente.
- ¿Alrededor del 95% de los\(y\) valores se encuentran entre qué dos valores? Estos valores son ________________. Los\(z\) puntajes -son ________________ respectivamente.
- ¿Alrededor del 99.7% de los\(y\) valores se encuentran entre qué dos valores? Estos valores son ________________. Los\(z\) puntajes -son ________________, respectivamente.
Contestar
- Alrededor del 68% de los valores se encuentran entre 166.02 y 178.7. Las\(z\) puntuaciones -son —1 y 1.
- Alrededor del 95% de los valores se encuentran entre 159.68 y 185.04. Las\(z\) puntuaciones -son —2 y 2.
- Alrededor del 99.7% de los valores se encuentran entre 153.34 y 191.38. Las\(z\) puntuaciones -son —3 y 3.
Ejercicio\(\PageIndex{6}\)
Los puntajes en un examen de ingreso a la universidad tienen una distribución normal aproximada con media,\(\mu = 52\) puntos y una desviación estándar,\(\sigma = 11\) puntos.
- ¿Alrededor del 68% de los\(y\) valores se encuentran entre qué dos valores? Estos valores son ________________. Los\(z\) puntajes -son ________________, respectivamente.
- ¿Alrededor del 95% de los\(y\) valores se encuentran entre qué dos valores? Estos valores son ________________. Los\(z\) puntajes -son ________________, respectivamente.
- ¿Alrededor del 99.7% de los\(y\) valores se encuentran entre qué dos valores? Estos valores son ________________. Los\(z\) puntajes -son ________________, respectivamente.
- Contestar a
-
Alrededor del 68% de los valores se encuentran entre los valores 41 y 63. Las\(z\) puntuaciones -son —1 y 1, respectivamente.
- Respuesta b
-
Alrededor del 95% de los valores se encuentran entre los valores 30 y 74. Las\(z\) puntuaciones -son —2 y 2, respectivamente.
- Respuesta c
-
Alrededor del 99.7% de los valores se encuentran entre los valores 19 y 85. Las\(z\) puntuaciones -son —3 y 3, respectivamente.
Resumen
A\(z\) -score es un valor estandarizado. Su distribución es la normal estándar,\(Z \sim N(0,1)\). The mean of the \(z\)-scores is zero and the standard deviation is one. If \(y\) is the z -score para un valor\(x\) from the normal distribution \(N(\mu, \sigma)\) then \(z\) tells you how many standard deviations \(x\) is above (greater than) or below (less than) \(\mu\).
Revisión de Fórmula
\(Z \sim N(0, 1)\)
\(z = a\)valor estandarizado (\(z\)-score)
media = 0; desviación estándar = 1
Para encontrar el percentil\(K\) th de\(X\) cuando se conocen los\(z\) -scores:
\(k = \mu + (z)\sigma\)
\(z\)-puntuación:\(z = \dfrac{x-\mu}{\sigma}\)
\(Z =\)la variable aleatoria para z -scores
\(Z \sim N(0, 1)\)
Glosario
- Distribución Normal Estándar
- una variable aleatoria continua (RV)\(X \sim N(0, 1)\); cuando\(X\) sigue la distribución normal estándar, a menudo se anota como\ (Z\ sim N (0, 1)\.
- \(z\)-puntuación
- la transformación lineal de la forma\(z = \dfrac{x-\mu}{\sigma}\); si esta transformación se aplica a cualquier distribución normal\(X \sim N(\mu, \sigma\) el resultado es la distribución normal estándar\(Z \sim N(0,1)\). Si esta transformación se aplica a algún valor específico\(x\) del RV con media\(\mu\) y desviación estándar\(\sigma\), el resultado se denomina\(z\) -score de\(x\). El\(z\) -score nos permite comparar datos que normalmente se distribuyen pero que se escalan de manera diferente.
Referencias
- “Presión Arterial de Hombres y Hembras”. StatCruch, 2013. Disponible en línea en http://www.statcrunch.com/5.0/viewre...reportid=11960 (consultado el 14 de mayo de 2013).
- “El uso de herramientas epidemiológicas en poblaciones afectadas por conflictos: recursos educativos de acceso abierto para formuladores de políticas: Cálculo de puntuaciones z”. London School of Hygiene and Tropical Medicine, 2009. Disponible en línea en http://conflict.lshtm.ac.uk/page_125.htm (consultado el 14 de mayo de 2013).
- “2012 Reporte de Perfil de Grupo Total de Adultos Mayores con destino a la Universidad”. CollegeBoard, 2012. Disponible en línea en media.collegedigita... Group-2012.pdf (consultado el 14 de mayo de 2013).
- “Digest of Education Statistics: Puntuación ACT promedio y desviaciones estándar por sexo y raza/etnia y porcentaje de tomadores de exámenes ACT, por rangos de puntaje compuestos seleccionados y campos de estudio planificados: Años seleccionados, 1995 a 2009.” Centro Nacional de Estadísticas Educativas. Disponible en línea en nces.ed.gov/programas/digest/d... s/dt09_147.asp (consultado el 14 de mayo de 2013).
- Datos del San Jose Mercury News.
- Datos de El Almanaque Mundial y Libro de Hechos.
- “Lista de estadios por aforo”. Wikipedia. Disponible en línea en es.wikipedia.org/wiki/list_o... ms_by_capacity (consultado el 14 de mayo de 2013).
- Datos de la Asociación Nacional de Basquetbol. Disponible en línea en www.nba.com (consultado el 14 de mayo de 2013).


