12.4: La ecuación de regresión
- Page ID
- 153220
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los datos rara vez se ajustan exactamente a una línea recta. Por lo general, debes estar satisfecho con predicciones aproximadas. Por lo general, tiene un conjunto de datos cuyo gráfico de dispersión parece “encajar” en una línea recta. Esto se llama Línea de Mejor Ajuste o Línea de Mínimos Cuadrados.
Ejercicio colaborativo
Si conoces la longitud del dedo meñique (más pequeño) de una persona, ¿crees que podrías predecir la altura de esa persona? Recopile datos de su clase (meñique longitud del dedo, en pulgadas). La variable independiente,\(x\), es la longitud del dedo meñique y la variable dependiente,\(y\), es la altura. Para cada conjunto de datos, graficar los puntos en papel cuadrificado. Haz tu gráfica lo suficientemente grande y usa una regla. Después “a ojo” dibuja una línea que parece “encajar” los datos. Para tu línea, elige dos puntos convenientes y úsalos para encontrar la pendiente de la línea. Encuentra la\(y\) intersección de la línea extendiendo tu línea para que cruce el\(y\) eje. Usando las pendientes y las\(y\) -intercepciones, escribe tu ecuación de “mejor ajuste”. ¿Crees que todos tendrán la misma ecuación? ¿Por qué o por qué no? Según su ecuación, ¿cuál es la altura predicha para una longitud meñique de 2.5 pulgadas?
Ejemplo\(\PageIndex{1}\)
Una muestra aleatoria de 11 estudiantes de estadística produjo los siguientes datos, donde\(x\) se encuentra la puntuación del tercer examen sobre 80, y\(y\) es la puntuación final del examen sobre 200. ¿Puedes predecir la puntuación final del examen de un estudiante aleatorio si conoces la puntuación del tercer examen?
| \(x\)(tercer examen) | \(y\)(puntaje final del examen) |
|---|---|
| \ (x\) (tercer puntaje del examen) ">65 | \ (y\) (puntaje final del examen) ">175 |
| \ (x\) (tercer puntaje del examen) ">67 | \ (y\) (puntaje final del examen) ">133 |
| \ (x\) (tercer puntaje del examen) ">71 | \ (y\) (puntaje final del examen) ">185 |
| \ (x\) (tercer puntaje del examen) ">71 | \ (y\) (puntaje final del examen) ">163 |
| \ (x\) (tercer puntaje del examen) ">66 | \ (y\) (puntaje final del examen) ">126 |
| \ (x\) (tercer puntaje del examen) ">75 | \ (y\) (puntaje final del examen) ">198 |
| \ (x\) (tercer puntaje del examen) ">67 | \ (y\) (puntaje final del examen) ">153 |
| \ (x\) (tercer puntaje del examen) ">70 | \ (y\) (puntaje final del examen) ">163 |
| \ (x\) (tercer puntaje del examen) ">71 | \ (y\) (puntaje final del examen) ">159 |
| \ (x\) (tercer puntaje del examen) ">69 | \ (y\) (puntaje final del examen) ">151 |
| \ (x\) (tercer puntaje del examen) ">69 | \ (y\) (puntaje final del examen) ">159 |
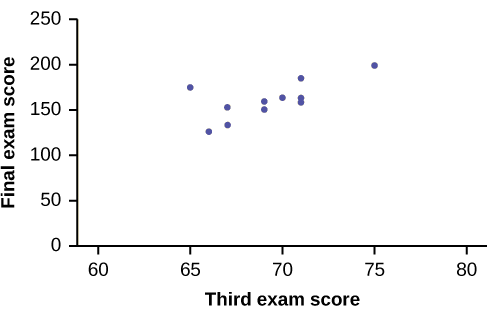
Ejercicio\(\PageIndex{1}\)
Los buceadores tienen tiempos máximos de buceo que no pueden superar cuando van a diferentes profundidades. Los datos de la Tabla muestran diferentes profundidades con los tiempos máximos de inmersión en minutos. Usa tu calculadora para encontrar la línea de regresión de mínimos cuadrados y predecir el tiempo máximo de inmersión para 110 pies.
| \(X\)(profundidad en pies) | \(Y\)(tiempo máximo de inmersión) |
|---|---|
| \ (X\) (profundidad en pies) ">50 | \ (Y\) (tiempo máximo de inmersión) ">80 |
| \ (X\) (profundidad en pies) ">60 | \ (Y\) (tiempo máximo de inmersión) ">55 |
| \ (X\) (profundidad en pies) ">70 | \ (Y\) (tiempo máximo de inmersión) ">45 |
| \ (X\) (profundidad en pies) ">80 | \ (Y\) (tiempo máximo de inmersión) ">35 |
| \ (X\) (profundidad en pies) ">90 | \ (Y\) (tiempo máximo de inmersión) ">25 |
| \ (X\) (profundidad en pies) ">100 | \ (Y\) (tiempo máximo de inmersión) ">22 |
Contestar
\(\hat{y} = 127.24 – 1.11x\)
A 110 pies, un buceador solo podía bucear por cinco minutos.
La puntuación del tercer examen,\(x\), es la variable independiente y la calificación final del examen,\(y\), es la variable dependiente. Vamos a trazar una línea de regresión que mejor “se ajuste” a los datos. Si cada uno de ustedes encajara una línea “a ojo”, dibujaría líneas diferentes. Podemos usar lo que se llama una línea de regresión de mínimos cuadrados para obtener la línea de mejor ajuste.
Considera el siguiente diagrama. Cada punto de datos es de la forma (\(x, y\)) y cada punto de la línea de mejor ajuste usando regresión lineal de mínimos cuadrados tiene la forma (\(x, \hat{y}\)).
El\(\hat{y}\) se lee "\(y\)sombrero” y es el valor estimado de\(y\). Es el valor de\(y\) obtenido usando la línea de regresión. Generalmente no es igual a\(y\) partir de datos.
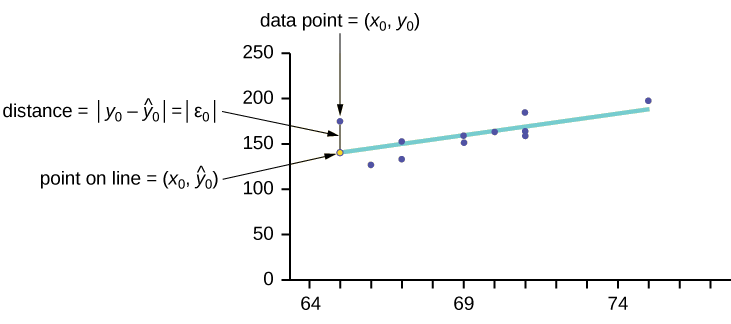
Al término\(y_{0} – \hat{y}_{0} = \varepsilon_{0}\) se le llama el “error” o residual. No es un error en el sentido de un error. El valor absoluto de un residual mide la distancia vertical entre el valor real de\(y\) y el valor estimado de\(y\). En otras palabras, mide la distancia vertical entre el punto de datos real y el punto predicho en la línea.
Si el punto de datos observado se encuentra por encima de la línea, el residuo es positivo y la línea subestima el valor de datos real para\(y\). Si el punto de datos observado se encuentra por debajo de la línea, el residuo es negativo y la línea sobreestima ese valor de datos real para\(y\).
En el diagrama de la Figura,\(y_{0} – \hat{y}_{0} = \varepsilon_{0}\) se encuentra el residual para el punto mostrado. Aquí el punto se encuentra por encima de la línea y el residual es positivo.
\(\varepsilon =\)la letra griega épsilon
Para cada punto de datos, se pueden calcular los residuos o errores,\(y_{i} - \hat{y}_{i} = \varepsilon_{i}\) para\(i = 1, 2, 3, ..., 11\).
Cada uno\(|\varepsilon|\) es una distancia vertical.
Para el ejemplo sobre las puntuaciones del tercer examen y las calificaciones finales del examen para los 11 estudiantes de estadística, hay 11 puntos de datos. Por lo tanto, hay 11\(\varepsilon\) valores. Si cuadras cada uno\(\varepsilon\) y agregas, obtienes
\[(\varepsilon_{1})^{2} + (\varepsilon_{2})^{2} + \dotso + (\varepsilon_{11})^{2} = \sum^{11}_{i = 1} \varepsilon^{2} \label{SSE}\]
La ecuación\ ref {SSE} se llama la Suma de Errores Cuadrados (SSE).
Mediante el cálculo, se pueden determinar los valores de\(a\) y\(b\) que hacen que el SSE sea mínimo. Cuando haces el SSE un mínimo, has determinado los puntos que están en la línea de mejor ajuste. Resulta que la línea de mejor ajuste tiene la ecuación:
\[\hat{y} = a + bx\]
donde
- \(a = \bar{y} - b\bar{x}\)y
- \(b = \dfrac{\sum(x - \bar{x})(y - \bar{y})}{\sum(x - \bar{x})^{2}}\).
Las medias muestrales de los\(x\) valores y los\(x\) valores son\(\bar{x}\) y\(\bar{y}\), respectivamente. La línea de mejor ajuste siempre pasa por el punto\((\bar{x}, \bar{y})\).
La pendiente se\(b\) puede escribir como\(b = r\left(\dfrac{s_{y}}{s_{x}}\right)\) donde\(s_{y} =\) la desviación estándar de los\(y\) valores y\(s_{x} =\) la desviación estándar de los\(x\) valores. \(r\)es el coeficiente de correlación, que se discute en la siguiente sección.
Criterios de mínimos cuadrados para el mejor ajuste
El proceso de ajuste de la línea de mejor ajuste se llama regresión lineal. La idea detrás de encontrar la línea que mejor se ajusta se basa en el supuesto de que los datos están dispersos alrededor de una línea recta. El criterio para la línea de mejor ajuste es que se minimalice la suma de los errores cuadrados (SSE), es decir, se haga lo más pequeña posible. Cualquier otra línea que elija tendría un SSE más alto que la línea de mejor ajuste. Esta línea de mejor ajuste se llama la línea de regresión de mínimos cuadrados.
Nota
Las hojas de cálculo de computadora, el software estadístico y muchas calculadoras pueden calcular rápidamente la línea que mejor se ajusta y crear las gráficas. Los cálculos tienden a ser tediosos si se hacen a mano. Al final de esta sección se muestran las instrucciones para usar las calculadoras TI-83, TI-83+ y TI-84+ para encontrar la línea que mejor se ajusta y crear una gráfica de dispersión.
EJEMPLO TERCER EXAMEN vs
La gráfica de la línea de mejor ajuste para el ejemplo de tercer examen/examen final es la siguiente:
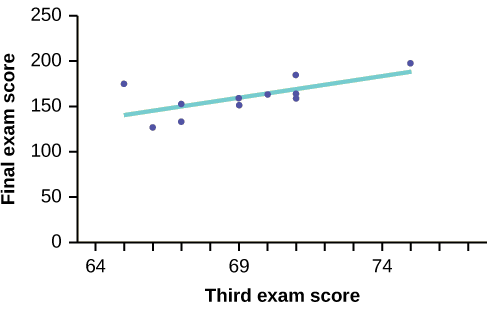
La línea de regresión de mínimos cuadrados (línea de mejor ajuste) para el ejemplo de tercer examen/examen final tiene la ecuación:
\[\hat{y} = -173.51 + 4.83x\]
RECORDATORIO
Recuerda, siempre es importante trazar primero un diagrama de dispersión. Si la gráfica de dispersión indica que existe una relación lineal entre las variables, entonces es razonable usar una línea de mejor ajuste para hacer predicciones para\(y\) dadas\(x\) dentro del dominio de\(x\) -valores en los datos de muestra, pero no necesariamente para x -valores fuera ese dominio. Podrías usar la línea para predecir la puntuación final del examen para un estudiante que obtuvo una calificación de 73 en el tercer examen. NO debes usar la línea para predecir la puntuación final del examen para un estudiante que obtuvo una nota de 50 en el tercer examen, porque 50 no está dentro del dominio de los\(x\) -valores en los datos de la muestra, que están entre 65 y 75.
Comprensión de la pendiente
La pendiente de la línea,\(b\), describe cómo se relacionan los cambios en las variables. Es importante interpretar la pendiente de la línea en el contexto de la situación representada por los datos. Deberías poder escribir una oración interpretando la pendiente en inglés llano.
INTERPRETACIÓN DE LA PENDIENTE: La pendiente de la línea de mejor ajuste nos dice cómo cambia la variable dependiente (\(y\)) por cada incremento unitario en la variable independiente (\(x\)), en promedio.
EJEMPLO TERCER EXAMEN
Pendiente: La pendiente de la línea es\(b = 4.83\).
Interpretación: Para un incremento de un punto en la puntuación del tercer examen, la puntuación del examen final aumenta en 4.83 puntos, en promedio.
USANDO LA CALCULADORA TI-83, 83+, 84, 84+
Uso de la Prueba T de Regresión Lineal: LineRegtTest
- En el editor de listas STAT, ingrese los\(X\) datos en la lista L1 y los datos Y en la lista L2, emparejados para que los valores correspondientes (\(x,y\)) estén uno al lado del otro en las listas. (Si se repite un par de valores en particular, ingréselo tantas veces como aparezca en los datos).
- En el menú PRUEBAS DE STAT, desplácese hacia abajo con el cursor para seleccionar el LineGTTest. (Tenga cuidado de seleccionar LineGTTest, ya que algunas calculadoras también pueden tener un elemento diferente llamado LinregTint.)
- En la pantalla de entrada LinregtTest ingrese: Xlist: L1; Ylist: L2; Freq: 1
- En la siguiente línea, en el símbolo\(\beta\) o\(\rho\), resalte "\(\neq 0\)" y presione ENTRAR
- Deje la línea para “RegEq:” en blanco
- Resalte Calcular y pulse INTRO.

La pantalla de salida contiene mucha información. Por ahora nos centraremos en algunos ítems de la salida, y volveremos más tarde a los otros ítems.
Dice la segunda línea\(y = a + bx\). Desplácese hacia abajo para encontrar los valores\(a = -173.513\), y\(b = 4.8273\); la ecuación de la línea de mejor ajuste es\(\hat{y} = -173.51 + 4.83x\)
Los dos elementos en la parte inferior son\(r_{2} = 0.43969\) y\(r = 0.663\). Por ahora, solo anote dónde encontrar estos valores; los discutiremos en las dos secciones siguientes.
Graficar el diagrama de dispersión y la línea de regresión
- Estamos asumiendo que sus\(X\) datos ya están ingresados en la lista L1 y sus\(Y\) datos están en la lista L2
- Presione 2do STATPLOT ENTER para usar la Parcela 1
- En la pantalla de entrada para PLAZAR 1, resalte On y presione ENTRAR
- Para TYPE: resalte el primer icono que es el diagrama de dispersión y presione ENTRAR
- Indicar Xlist: L1 e Ylist: L2
- Para Mark: no importa qué símbolo resaltes.
- Presione la tecla ZOOM y luego el número 9 (para el elemento del menú “ZoomStat”); la calculadora ajustará la ventana a los datos
- Para graficar la línea de mejor ajuste, presione la tecla\(Y =\) "" y escriba la ecuación\(-173.5 + 4.83X\) en la ecuación Y1. (La\(X\) clave queda inmediatamente a la izquierda de la tecla STAT). Presione ZOOM 9 nuevamente para graficarlo.
- Opcional: Si desea cambiar la ventana de visualización, presione la tecla VENTANA. Ingrese su ventana deseada usando Xmin, Xmax, Ymin, Ymax
Nota
Otra forma de graficar la línea después de crear una gráfica de dispersión es usar LinregtTest.
- Asegúrate de haber hecho el diagrama de dispersión. Compruébalo en tu pantalla.
- Ve a LineGttest e ingresa a las listas.
- En RegEq: presione VARS y flecha hacia Y-VARS. Presiona 1 para 1:Función. Presione 1 para 1:Y1. Después flecha hacia abajo para Calcular y hacer el cálculo para la línea de mejor ajuste.
- Prensa\(Y = (\text{you will see the regression equation})\).
- Presione GRAPH. Se trazará la línea”.
El coeficiente de correlación\(r\)
Además de mirar el diagrama de dispersión y ver que una línea parece razonable, ¿cómo se puede saber si la línea es un buen predictor? Utilizar el coeficiente de correlación como otro indicador (además de la gráfica de dispersión) de la fuerza de la relación entre\(x\) y\(y\). El coeficiente de correlación\(r\), desarrollado por Karl Pearson a principios del siglo XX, es numérico y proporciona una medida de fuerza y dirección de la asociación lineal entre la variable independiente\(x\) y la variable dependiente\(y\).
El coeficiente de correlación se calcula como
\[r = \dfrac{n \sum(xy) - \left(\sum x\right)\left(\sum y\right)}{\sqrt{\left[n \sum x^{2} - \left(\sum x\right)^{2}\right] \left[n \sum y^{2} - \left(\sum y\right)^{2}\right]}}\]
donde\(n =\) el número de puntos de datos.
Si sospecha una relación lineal entre\(x\) y\(y\), entonces\(r\) puede medir qué tan fuerte es la relación lineal.
Lo que nos\(r\) dice el VALOR:
- El valor de siempre\(r\) está entre —1 y +1: —1 ≤ r ≤ 1.
- El tamaño de la correlación\(r\) indica la fuerza de la relación lineal entre\(x\) y\(y\). Los valores\(r\) cercanos a —1 o a +1 indican una relación lineal más fuerte entre\(x\) y\(y\).
- Si no\(r = 0\) hay absolutamente ninguna relación lineal entre\(x\) y\(y\) (sin correlación lineal).
- Si\(r = 1\), hay perfecta correlación positiva. Si\(r = -1\), hay correlación negativa perfecta. En ambos casos, todos los puntos de datos originales se encuentran en línea recta. Por supuesto, en el mundo real, esto generalmente no sucederá.
Lo que nos\(r\) dice el SIGNO:
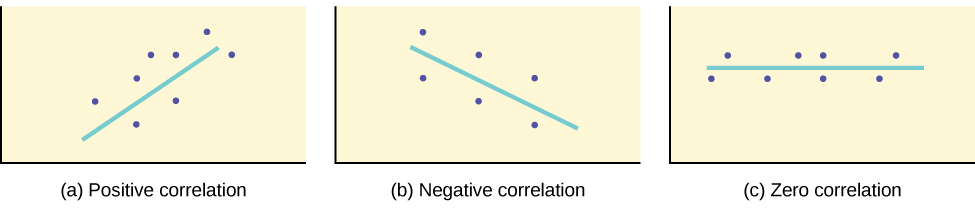
- Un valor positivo de\(r\) significa que cuando\(x\) aumenta,\(y\) tiende a aumentar y cuando\(x\) disminuye,\(y\) tiende a disminuir (correlación positiva).
- Un valor negativo de\(r\) significa que cuando\(x\) aumenta,\(y\) tiende a disminuir y cuando\(x\) disminuye,\(y\) tiende a aumentar (correlación negativa).
- El signo de\(r\) es el mismo que el signo de la pendiente,\(b\), de la línea de mejor ajuste.
Nota
Fuerte correlación no sugiere que\(x\) causas\(y\) o\(y\) causas\(x\). Decimos “la correlación no implica causalidad”.
La fórmula para\(r\) looks formidables. Sin embargo, las hojas de cálculo de computadora, el software estadístico y muchas calculadoras pueden calcular rápidamente\(r\). El coeficiente de correlación\(r\) es el elemento inferior en las pantallas de salida para el LineGTEST en la calculadora TI-83, TI-83+ o TI-84+ (consulte la sección anterior para obtener instrucciones).
El coeficiente de determinación
La variable\(r^{2}\) se denomina coeficiente de determinación y es el cuadrado del coeficiente de correlación, pero generalmente se establece como un porcentaje, más que en forma decimal. Tiene una interpretación en el contexto de los datos:
- \(r^{2}\), cuando se expresa como un porcentaje, representa el porcentaje de variación en la variable dependiente (predicha)\(y\) que puede explicarse por la variación en la variable independiente (explicativa)\(x\) utilizando la línea de regresión (mejor ajuste).
- \(1 - r^{2}\), cuando se expresa como un porcentaje, representa el porcentaje de variación en\(y\) que NO se explica por la variación en el\(x\) uso de la línea de regresión. Esto puede verse como la dispersión de los puntos de datos observados sobre la línea de regresión.
Considera el tercer examen/ejemplo de examen final introducido en la sección anterior
- La línea de mejor ajuste es:\(\hat{y} = -173.51 + 4.83x\)
- El coeficiente de correlación es\(r = 0.6631\)
- El coeficiente de determinación es\(r^{2} = 0.6631^{2} = 0.4397\)
- Interpretación de\(r^{2}\) en el contexto de este ejemplo:
- Aproximadamente 44% de la variación (0.4397 es aproximadamente 0.44) en las calificaciones del examen final puede explicarse por la variación en las calificaciones del tercer examen, utilizando la línea de regresión de mejor ajuste.
- Por lo tanto, aproximadamente 56% de la variación (\(1 - 0.44 = 0.56\)) en las calificaciones del examen final NO puede explicarse por la variación en las calificaciones del tercer examen, utilizando la línea de regresión de mejor ajuste. (Esto se ve como la dispersión de los puntos alrededor de la línea.)
Resumen
Una línea de regresión, o una línea de mejor ajuste, puede dibujarse en un gráfico de dispersión y usarse para predecir resultados para las\(y\) variables\(x\) y en un conjunto de datos o datos de muestra dados. Hay varias formas de encontrar una línea de regresión, pero generalmente se usa la línea de regresión de mínimos cuadrados porque crea una línea uniforme. Los residuales, también llamados “errores”, miden la distancia desde el valor real de\(y\) y el valor estimado de\(y\). La Suma de Errores Cuadrados, cuando se establece en su mínimo, calcula los puntos en la línea de mejor ajuste. Las líneas de regresión se pueden usar para predecir valores dentro del conjunto de datos dado, pero no deben usarse para hacer predicciones para valores fuera del conjunto de datos.
El coeficiente de correlación\(r\) mide la fuerza de la asociación lineal entre\(x\) y\(y\). La variable\(r\) tiene que estar entre —1 y +1. Cuando\(r\) es positivo, el\(x\) y\(y\) tenderá a aumentar y disminuir juntos. Cuando\(r\) sea negativo,\(x\) aumentará y\(y\) disminuirá, o lo contrario,\(x\) disminuirá y\(y\) aumentará. El coeficiente de determinación\(r^{2}\), es igual al cuadrado del coeficiente de correlación. Cuando se expresa como un porcentaje,\(r^{2}\) representa el porcentaje de variación en la variable dependiente\(y\) que puede explicarse por la variación en la variable independiente\(x\) utilizando la línea de regresión.
Glosario
- Coeficiente de Correlación
- una medida desarrollada por Karl Pearson (principios del siglo XX) que da la fuerza de asociación entre la variable independiente y la variable dependiente; la fórmula es:
\[r = \dfrac{n \sum xy - \left(\sum x\right) \left(\sum y\right)}{\sqrt{\left[n \sum x^{2} - \left(\sum x\right)^{2}\right] \left[n \sum y^{2} - \left(\sum y\right)^{2}\right]}}\]
donde\(n\) está el número de puntos de datos. El coeficiente no puede ser superior a 1 ni inferior a —1. Cuanto más cerca esté el coeficiente de ±1, más fuerte será la evidencia de una relación lineal significativa entre\(x\) y\(y\).


