9.3: El producto cruzado y las cantidades rotacionales
- Page ID
- 128181
El cruce, o vector, producto de dos vectores\(\vec A\) y\(\vec B\) se denota por\(\vec{A} \times \vec{B}\). Se define como un vector perpendicular a ambos\(\vec A\) y\(\vec B\) (es decir, al plano que los contiene a ambos), con una magnitud dada por
\[ |\vec{A} \times \vec{B}|=A B \sin \theta \label{eq:9.9} \]
donde\(A\) y\(B\) son las magnitudes de\(\vec A\) y\(\vec B\), respectivamente, y\(\theta\) es el ángulo entre\(\vec A\) y\(\vec B\), cuando se dibujan ya sea con el mismo origen o punta a cola.
La dirección específica de\(\vec A \times \vec B\) depende de la orientación relativa de los dos vectores. Básicamente, si\(\vec B\) es en sentido antihorario desde\(\vec A\), al mirar hacia abajo sobre el plano en el que se encuentran, asumiendo que se dibujan con un origen común, entonces\(\vec{A} \times \vec{B}\) apunta hacia arriba desde ese plano; de lo contrario, apunta hacia abajo (hacia el plano). También se puede utilizar la llamada regla de la mano derecha, ilustrada en la Figura\(\PageIndex{1}\) para averiguar la dirección de\(\vec{A} \times \vec{B}\). Obsérvese que, por esta definición, la dirección de\(\vec{A} \times \vec{B}\) es la opuesta a la dirección de\(\vec{B} \times \vec{A}\) (como también se ilustra en la Figura\(\PageIndex{1}\)). De ahí que el producto cruzado no sea conmutativo: el orden de los factores marca la diferencia.
\[ \vec{A} \times \vec{B}=-\vec{B} \times \vec{A} \label{eq:9.10} \]
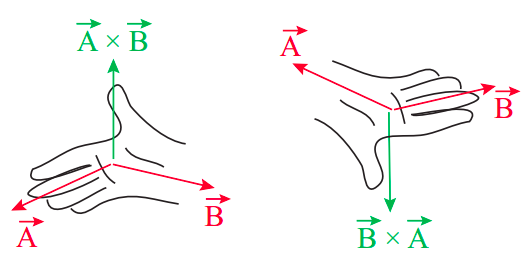
De la Ecuación (\ ref {eq:9.10}) se deduce que el producto cruzado de cualquier vector consigo mismo debe ser cero. De hecho, según la Ecuación (\ ref {eq:9.9}), el producto cruzado de dos vectores cualesquiera que sean paralelos entre sí es cero, ya que en ese caso\(\theta\) = 0, y\(\sin 0\) = 0. En este sentido, el producto cruzado es lo opuesto al producto punto que introdujimos en el Capítulo 7: es máximo cuando los vectores que se multiplican son ortogonales, y cero cuando son paralelos. (Y, por supuesto, el resultado de\(\vec{A} \times \vec{B}\) es un vector, mientras que\(\vec{A} \cdot \vec{B}\) es un escalar).
Además de no ser conmutativo, el producto cruzado tampoco tiene la propiedad asociativa de la multiplicación ordinaria:\(\vec{A} \times(\vec{B} \times \vec{C}) \) es diferente de\((\vec{A} \times \vec{B}) \times \vec{C} \). Esto se puede ver fácilmente por el hecho de que\(\vec A = \vec B\), si, la segunda expresión será cero, pero la primera generalmente será distinta de cero (ya que no\(\vec{A} \times \vec{C}\) es paralela, sino perpendicular a\(\vec A\)).
A pesar de estas rarezas, el producto cruzado es extremadamente útil en física. Lo usaremos para definir el vector\(\vec L\) de momento angular de una partícula, relativo a un punto O, de la siguiente manera:
\[ \vec{L}=\vec{r} \times \vec{p}=m \vec{r} \times \vec{v} \label{eq:9.11} \]
donde\(\vec r\) está el vector de posición de la partícula, relativo al punto O. Esta definición nos da un vector constante para una partícula que se mueve en línea recta, como se discutió en la sección anterior: la magnitud de\(\vec L\), según la Ecuación (\ ref {eq:9.9}) será\(mrv \sin \theta\), que, como se muestra en Figura 9.2.1, no cambia a medida que la partícula se mueve. En cuanto a la dirección, siempre es perpendicular al plano que contiene\(\vec r\) y\(\vec v\) (el plano del papel, en la Figura 9.2.1), y si imagina moverse\(\vec v\) al punto O, manteniéndolo paralelo a sí mismo, y aplicar la regla de la derecha, verá que\(\vec L\) en Figura 9.2.1, debe apuntar en todo momento al plano del papel.
Para ver cómo funciona la definición (\ ref {eq:9.11}) para una partícula que se mueve en círculo, considere nuevamente la situación mostrada en la Figura 8.4.2 en el capítulo anterior, pero ahora extiéndala a tres dimensiones, como en la Figura\(\PageIndex{2}\), en la página siguiente. Es sencillo verificar que, para la dirección de movimiento mostrada, el producto cruzado siempre\(\vec{r} \times \vec{v}\) apuntará hacia arriba, a lo largo del\(z\) eje positivo. Además, dado que\(\vec r\) y\(\vec v\) siempre permanecen perpendiculares, la magnitud de\(\vec L\), por Ecuación (\ ref {eq:9.9}), siempre será\(|\vec{L}|=m R|\vec{v}|\) .Tomando nota de\(I = mR^2\) y de la Ecuación (8.4.12), vemos que tenemos entonces
\[ |\vec{L}|=\left(m R^{2}\right) \frac{|\vec{v}|}{R}=I|\omega| \label{eq:9.12} \]
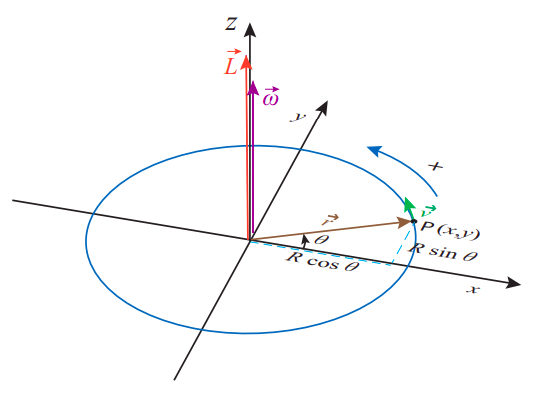
Esto sugiere que debemos definir el vector de velocidad angular\(\vec \omega\), como un vector de magnitud\(|\omega|\), apuntando a lo largo del\(z\) eje positivo si el movimiento en el\(y\) plano\(x\) - es en sentido antihorario como se ve desde arriba (y en la dirección opuesta de lo contrario). Entonces esto se mantendrá como una ecuación vectorial:
\[ \vec{L}=I \vec{\omega} \label{eq:9.13} .\]
Puede parecer una elección muy extraña tener el punto de velocidad angular a lo largo del\(z\) eje, cuando la partícula se mueve en el\(y\) plano\(x\) -, pero de cierta manera tiene sentido. Supongamos que la partícula se mueve con velocidad angular constante: las direcciones de\(\vec r\) y\(\vec v\) están cambiando constantemente, pero\(\vec \omega\) apunta a lo largo de la\(z\) dirección positiva, que permanece fija en todo momento
Hay algunas otras cosas ordenadas con las que podemos hacer\(\vec \omega\) como se definió anteriormente. Considera el producto cruzado\(\vec{\omega} \times \vec{r}\). La inspección de la Figura\(\PageIndex{2}\) y de la Ecuación (8.4.12) muestra que no es otra cosa que el vector de velocidad ordinaria,\(\vec v\):
\[ \vec{v}=\vec{\omega} \times \vec{r} \label{eq:9.14} .\]
También podemos tomar la derivada de\(\vec \omega\) para obtener el vector de aceleración angular\(\vec \alpha\), de manera que la Ecuación (8.4.9) se mantendrá como una ecuación vectorial:
\[ \vec{\alpha}=\lim _{\Delta t \rightarrow 0} \frac{\vec{\omega}(t+\Delta t)-\vec{\omega}(t)}{d t}=\frac{d \vec{\omega}}{d t} \label{eq:9.15} .\]
Para el movimiento representado en la Figura\(\PageIndex{2}\), el vector\(\vec \alpha\) apuntará a lo largo del\(z\) eje positivo si el vector\(\vec \omega\) está creciendo (lo que significa que la partícula se está acelerando), y a lo largo del\(z\) eje negativo si\(\vec \omega\) está disminuyendo.
Una propiedad importante que tiene el producto cruzado es la propiedad distributiva con respecto a la suma:
\[ (\vec{A}+\vec{B}) \times \vec{C}=\vec{A} \times \vec{C}+\vec{B} \times \vec{C} \label{eq:9.16} .\]
Esto, resulta, es todo lo necesario para poder aplicar la regla de diferenciación del producto para calcular la derivada de un producto cruzado; solo hay que tener cuidado de no cambiar el orden de los factores al hacerlo. Entonces podemos tomar la derivada de ambos lados de la Ecuación (\ ref {eq:9.14}) para obtener una expresión para el vector de aceleración:
\ begin {align}
\ vec {a} =\ frac {d\ vec {v}} {d t} &=\ frac {d\ vec {\ omega}} {d t}\ veces\ vec {r} +\ vec {\ omega}\ veces\ frac {d\ vec {r}} {d t}\ nonumber\\
&=\ vec {alfa}\ veces\ vec {r} +\ vec {\ omega}\ veces\ vec {v}\ label {eq:9.17}.
\ end {align}
El primer término en el lado derecho,\(\vec{\alpha} \times \vec{r}\), se encuentra en el\(x\) -\(y\) plano, y es perpendicular a\(\vec r\); es, por lo tanto, tangencial al círculo. De hecho, mirando su magnitud, es claro que este es solo el vector de aceleración tangencial, que introduje (como escalar) en la Ecuación (8.4.13).
En cuanto al segundo término en (\ ref {eq:9.17})\(\vec \omega \times \vec v\), al señalar que\(\vec \omega\) y\(\vec v\) son siempre perpendiculares, está claro que su magnitud es\(|\omega||\vec{v}|=R \omega^{2}=v^{2} / R\) (haciendo uso de la Ecuación (8.4.12) nuevamente). Esta es solo la magnitud de la aceleración centrípeta que estudiamos en el capítulo anterior (sección 8.4). También, usando la regla de la derecha en Figura\(\PageIndex{2}\), se puede ver que\(\vec{\omega} \times \vec{v}\) siempre apunta hacia adentro, hacia el centro del círculo; es decir, a lo largo de la dirección de\(−\vec r\). Al juntar todo esto, podemos escribir este vector como justo\(−\omega^2 \vec r\), y todo el vector de aceleración como la suma de una componente tangencial y una centrípeta (radial), de la siguiente manera:
Para concluir esta sección, permítanme volver al vector de momento angular, y plantearme la pregunta de si, en general, el momento angular de un sistema giratorio, definido como la suma de la Ecuación (\ ref {eq:9.11}) sobre todas las partículas que componen el sistema, satisfará o no la ecuación vectorial\(\vec L = I\omega\). Hemos visto que esto efectivamente funciona para una partícula que se mueve en círculo. Por lo tanto, también funcionará para cualquier objeto que sea esencialmente plano, y que gire alrededor de un eje perpendicular al mismo, ya que en ese caso todas sus partes apenas se mueven en círculos alrededor de un centro común. Este fue el caso de la varilla delgada que consideramos en relación con la Figura 9.2.3 en la subsección anterior.
Sin embargo, si el sistema es un objeto tridimensional que gira alrededor de un eje arbitrario, el resultado generalmente\(\vec L = I\vec \omega\) no se mantiene. La razón es, matemáticamente, que el momento de inercia\(I\) se define (Ecuación (9.1.3)) en términos de las distancias de las partículas a un eje, mientras que el momento angular implica la distancia de la partícula a un punto. Para partículas a diferentes “alturas” a lo largo del eje de rotación, estas cantidades son diferentes. Se puede demostrar que, en el caso general, lo único que podemos decir es eso\(L_z = I\omega_z\), si llamamos\(z\) al eje de rotación y calculamos\(\vec L\) relativo a un punto sobre ese eje.
Por otro lado, si el eje de rotación es un eje de simetría del objeto, entonces solo\(\vec L\) tiene un\(z\) componente, y el resultado se\(\vec L = I\vec \omega\) mantiene como una ecuación vectorial. La mayoría de los sistemas que consideraremos este semestre estarán cubiertos bajo esta cláusula, o bajo la cláusula “esencialmente plana” mencionada anteriormente.
En lo que sigue generalmente asumiremos que\(I\) tiene solo un\(z\) componente, y bajaremos el subíndice\(z\) en la ecuación\(L_z = I\omega_z\), de manera que\(L\) y no necesariamente\(\omega\) serán las magnitudes de sus respectivos vectores, sino números que podrían ser positivos o negativos , dependiendo de la dirección de rotación (en sentido horario o antihorario). Esta es esencialmente la misma convención que usamos para vectores en una dimensión, como\(\vec a\) o\(\vec p\), en los primeros capítulos; está bien para todos los casos en los que el (dirección del) eje de rotación no cambia con el tiempo, que son las únicas situaciones que consideraremos este semestre.


