9.2: Momentum Angular

De vuelta en el capítulo 3 introdujimos el impulso de un objeto que se mueve en una dimensión como\(p = mv\), y encontramos que tenía la interesante propiedad de conservarse en colisiones entre objetos que conformaban un sistema aislado. Parece natural preguntarse si la cantidad rotacional correspondiente, formada multiplicando la “inercia rotacional”\(I\) y la velocidad angular\(\omega\), tiene también propiedades interesantes. Estamos tentativamente ¹ vamos a llamar a la cantidad impulso\(I\omega\) angular (para distinguirlo del “ordinario”, o impulso lineal,\(mv\)), y construir hacia una mejor comprensión, y una definición formal del mismo, en el resto de esta sección.

Dos cosas pronto son evidentes: una es que, a diferencia de la energía cinética rotacional, que era simplemente energía cinética simple, la cantidad\(I\omega\) realmente es diferente del momento ordinario, ya que tiene diferentes dimensiones (ver el factor “extra” de\(R\) en la Ecuación (\ ref {eq:9.4}) a continuación). La otra es que existen, de hecho, sistemas en la naturaleza donde esta cantidad parece permanecer constante a una buena aproximación. Por ejemplo, la Tierra girando alrededor de su eje, a un ritmo constante de\(2\pi\) radianes cada 24 horas, tiene, en virtud de eso, un momento angular constante (una constante\(I\) y\(\omega\)).

Lo mejor, sin embargo, es comenzar pensando en cómo definiríamos el “momento angular” para un sistema que consiste en una sola partícula, y luego construir a partir de ahí, como hemos estado haciendo todo el semestre con cada nuevo concepto. Para una partícula que se mueve en círculo, según el apartado anterior, el momento de inercia es justo\(I = mR^2\), y por lo tanto\(I\omega\) es justo\(mR^2\omega\). Usando la Ecuación (8.4.12), podemos escribir (la letra\(L\) es el símbolo convencional para el momento angular; ¡no lo confundas con una longitud!)

\[ L=I \omega=\pm m R|v| \quad \mathrm{ (particle \: moving \: in \: a \: circle) } \label{eq:9.4} \]

donde, por coherencia con nuestra convención de signos para\(\omega\), debemos usar el signo positivo si la rotación es en sentido antihorario, y el signo negativo si es en sentido horario.

De nuevo podemos pensar fácilmente en ejemplos en la naturaleza donde se conserva la cantidad (\ ref {eq:9.4}): por ejemplo, la luna, si la tratamos como una partícula que orbita la Tierra en una órbita aproximadamente circular ², tiene entonces un momento angular aproximadamente constante, como lo da la Ecuación (\ ref {eq:9.4}). Este ejemplo también es interesante porque ofrece un indicio de una diferencia importante entre el momento ordinario y el momento angular: parece que este último puede conservarse incluso en presencia de algún tipo de fuerzas externas (en este caso, la fuerza de gravedad debida a la Tierra que mantiene encendida la luna su órbita).

Por otro lado, no es inmediatamente obvio cómo generalizar la definición (9.4) a otro tipo de movimiento. Si simplemente intentamos algo así como\(L = mvr\), dónde\(r\) está la distancia a un eje fijo, o a un punto fijo, entonces encontramos que esto produce una cantidad que cambia constantemente, incluso para el sistema físico más simple posible, es decir, una partícula que se mueve en línea recta con velocidad constante. Sin embargo, nos gustaría definir de tal\(L\) manera que se mantendrá constante cuando, de hecho, nada en el estado real de movimiento de la partícula esté cambiando.

La forma de hacerlo, para una partícula que se mueve en línea recta, es definir\(L\) como el producto de los\(mv\) tiempos, no la distancia de la partícula a un punto, sino la distancia de la línea de movimiento de la partícula al punto considerado. La “línea de movimiento” es solo una línea recta que contiene el vector de velocidad en cualquier momento dado. La distancia entre una línea y un punto O es, por definición, la distancia más corta de O a cualquier punto de la línea; viene dada por la longitud de un segmento dibujado perpendicular a la línea a través del punto O.

Para una partícula que se mueve en círculo, la línea de movimiento en cualquier momento es tangente al círculo, y así la distancia entre la línea de movimiento y el centro del círculo es solo el radio\(R\), por lo que recuperamos la definición Ecuación (\ ref {eq:9.4}). Para el caso general, por otro lado, tenemos la situación que se muestra en la Figura\(\PageIndex{1}\): si la velocidad instantánea de la partícula es\(\vec v\), y dibujamos el vector de posición de la partícula,\(\vec r\), con el punto O como origen, entonces la distancia entre O y la línea de movimiento (a veces también llamada la distancia perpendicular entre O y la partícula) viene dada por\(r \sin \theta\), donde\(\theta\) está el ángulo entre los vectores\(\vec r\) y\(\vec v\).

Figura\(\PageIndex{1}\): Para una partícula que se mueve en línea recta, la distancia desde el punto O a la línea de movimiento de la partícula (línea discontinua) es igual a\(r \sin \theta\) en cada punto de la trayectoria (dos puntos posibles se muestran en la figura). La distancia es la longitud del segmento azul. La figura muestra que hay cierta libertad en elegir cómo\(\vec v\) se va a medir el ángulo\(\theta\) entre\(\vec r\) y, ya que el seno de\(\theta\) es el mismo que el seno de\(\pi - \theta\).

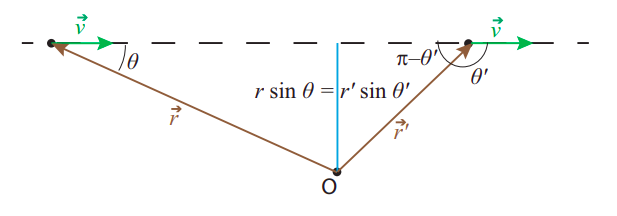
Por lo tanto, intentamos definir el momento angular relativo a un punto O como el producto

\[ L=\pm m r|v| \sin \theta \label{eq:9.5} \]

con el signo positivo si el punto O está a la izquierda de la línea de movimiento a medida que pasa la partícula (lo que corresponde al movimiento en sentido contrario a las agujas del reloj en el círculo), y negativo en caso contrario.

Hay dos cosas muy buenas de la definición (\ ref {eq:9.5}): la primera es que ya existe una operación matemática entre vectores, llamada vector, o cruz, producto, según la cual\(|L|\), como se define por (\ ref {eq:9.5}), simplemente ser dado por\(|\vec{r} \times \vec{p}| \), donde\(\vec{r} \times \vec{p} \) esta el producto cruzado de\(\vec r\) y\(\vec p\); voy a tener mucho más que decir sobre esto en la siguiente subsección. Lo segundo bueno es que, con esta definición, el momento angular se conservará en un tipo importante de proceso, a saber, una colisión que convierte el movimiento lineal en rotacional, como se ilustra en la Figura\(\PageIndex{2}\) siguiente.

Figura\(\PageIndex{2}\): Colisión entre dos partículas, 1 y 2, de masas iguales. La partícula 2 es atada por una cuerda sin masa al punto O. Después de la colisión, la partícula 1 está en reposo y la partícula 2 se mueve en el círculo mostrado.

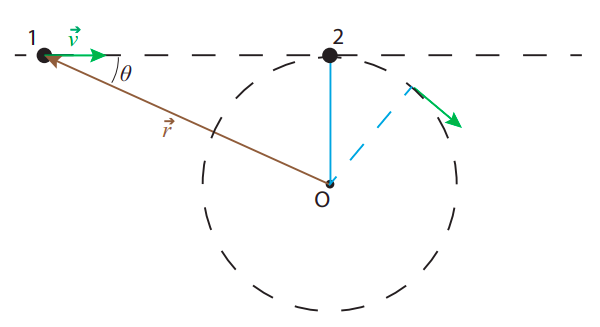
En la imagen, la partícula 1 se mueve inicialmente con velocidad constante\(\vec v\) y la partícula 2 está inicialmente en reposo, atada por una cuerda sin masa al punto O. Si las partículas tienen la misma masa, la conservación del impulso (ordinario) y la energía cinética significa que cuando chocan intercambian velocidades: la partícula 1 se detiene y la partícula 2 comienza a moverse hacia la derecha con la misma velocidad v, pero inmediatamente la cuerda comienza a tirar de ella y doblar su trayectoria en un círculo. Asumiendo una fricción insignificante entre la cuerda y el punto pivotante (y todas las superficies involucradas), la velocidad de la partícula 2 permanecerá constante a medida que gira, por conservación de la energía cinética, porque la tensión en la cuerda siempre es perpendicular al vector de desplazamiento de la partícula, por lo que no funciona en él.

Todo lo anterior significa que se conserva el momento angular: antes de la colisión era igual a\(−mvr \sin \theta = −mvR\) para la partícula 1, y 0 para la partícula 2; después de la colisión es cero para la partícula 1 y\(I\omega = mR^2\omega = −mRv\) para la partícula 2 (la nota\(\omega\) es negativa, porque la rotación es en sentido horario). También se conserva la energía cinética, por las razones argumentadas anteriormente. Por otro lado, el impulso ordinario solo se conserva hasta justo después de la colisión, cuando la cuerda comienza a tirar de la partícula 2, ya que esto representa una fuerza externa sobre el sistema.

Así que hemos encontrado una situación en la que el movimiento lineal se convierte en movimiento circular mientras que el momento angular, definido por la Ecuación (\ ref {eq:9.5}), se conserva, y esto a pesar de la presencia de una fuerza externa. Es cierto que, de hecho, pudimos resolver para el movimiento final sin hacer uso explícito de la conservación del momento angular: solo tuvimos que invocar la conservación del momento ordinario por la corta duración de la colisión, y la conservación de la energía cinética. Pero es fácil generalizar el problema representado en la Figura\(\PageIndex{2}\) a uno que no se puede resolver con estos métodos, sino que se puede resolver si el momento angular es constante. Supongamos que reemplazamos la partícula 2 y la cuerda por una varilla delgada de masa\(m\) y longitud\(l\) pivotada en un extremo. ¿Qué pasa ahora cuando la partícula 1 golpea la varilla?

Figura\(\PageIndex{3}\): Colisión entre una partícula que inicialmente se mueve con velocidad\(\vec v_1\) y una varilla de longitud\(l\) pivotada en un punto final. La partícula golpea la varilla perpendicularmente, en el otro extremo. Después de la colisión, la partícula se mueve a lo largo de la misma línea con velocidad\(\vec v_f\), y la varilla gira alrededor del punto O con una velocidad angular\(\omega\).

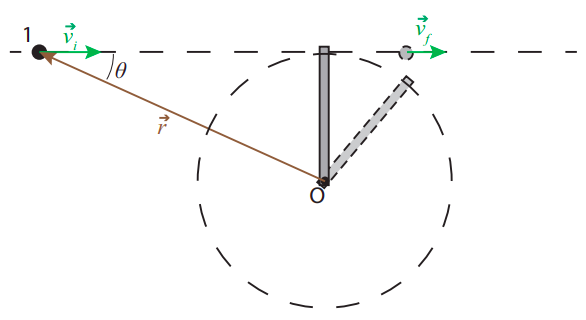
Si la partícula golpea la varilla perpendicularmente, y la colisión ocurre muy rápido (es decir, se termina antes de que la varilla tenga tiempo de moverse una distancia significativa), podemos suponer que la fuerza ejercida por la varilla sobre la partícula (una fuerza normal) está a lo largo de la línea de movimiento original, por lo que la partícula continuará moviéndose en esa línea. Por otro lado, esta vez no podemos descuidar la fuerza ejercida por el pivote sobre la barra durante el tiempo de colisión, ya que la barra es un solo objeto rígido. Esto significa que el sistema no está aislado durante la colisión, y no podemos confiar en la conservación ordinaria del momento.

Supongamos, sin embargo, que\(L\) se conserva el momento angular, así como la energía total (el pivote no funciona en el sistema, ya que no hay desplazamiento de ese punto). El momento angular inicial es\(L_i = −mv_il\). El momento angular final es\(−mv_{f}l\) para la partícula (nótese que, si la partícula rebota,\(v_f\) será negativa) y\(I\omega\) para la varilla. La energía cinética inicial es\(K_i = \frac{1}{2}mv^2_i\), y la energía cinética final es\(\frac{1}{2}mv^2_f\) para la partícula y\(\frac{1}{2}I\omega ^2\) para la varilla (recordar Ecuación (9.1.2), por lo que tenemos que resolver el sistema

\ begin {align}
-m v_ {i} l &=-m v_ {f} L+i\ omega\ nonumber\\
\ frac {1} {2} m v_ {i} ^ {2} &=\ frac {1} {2} m v_ {f} ^ {2} +\ frac {1} {2} I\ omega^ {2}\ etiqueta {ee q:9.6}
\ end {align}

La solución general, para valores arbitrarios de todas las constantes, es

\ begin {align}
v_ {f} &=\ frac {m l^ {2} -I} {m l^ {2} +I} v_ {i}\ nonumber\
\ omega&=-\ frac {2 m l} {m l^ {2} +I} v_ {i}\ etiqueta {eq:9.7}
\ end align {}

Tenga en cuenta que esto sí se reduce a nuestros resultados anteriores para la colisión de dos partículas si hacemos\(I = ml^2\) (lo que siempre se podría hacer, eligiendo la masa de la varilla,\(M\), apropiadamente). Por otro lado, como se indica al final de la subsección anterior, para general\(M\) tenemos\(I = \frac{1}{3}Ml^2\) para la varilla, así podemos cancelar\(l^2\) casi en todas partes y terminar con

\ begin {align}
v_ {f} &=\ frac {3 M-m} {3 m+m} v_ {i}\ nonumber\\
\ omega &=-\ frac {6 m} {3 m+m}\ frac {v_ {i}} {l}\ label {eq:9.8}
\ end {align}

En particular, vemos que si\(m = M\) la partícula continúa avanzando con 1/2 de su velocidad inicial, y la varilla gira con\(\omega = −(3/2)v_i/l\), que en realidad es una velocidad angular mayor que la que encontramos para el sistema en la Figura\(\PageIndex{2}\).

Este ejemplo muestra lo útil que puede ser la conservación del momento angular, pero, por supuesto, ¡todavía no sabemos realmente si el momento angular se conserva realmente en este problema! Voy a abordar esta cuestión muy importante —cuándo se conserva el momento angular— en la sección siguiente, es decir, después de haber desarrollado adecuadamente el momento angular como cantidad vectorial.

---

¹ Como veremos a continuación, en general\(I\omega\) es igual a un solo componente del vector de momento angular.

² Puedes echar un vistazo adelante en la Figura 10.1.1, en el siguiente capítulo, para ver qué tan buena aproximación podría ser esta!