9.4: Torque

Finalmente estamos en condiciones de responder a la pregunta, ¿cuándo se conserva el momento angular? Para ello, simplemente tomaremos la derivada de\(\vec L\) con respecto al tiempo, y usaremos las leyes de Newton para averiguar en qué circunstancias es igual a cero.

Comencemos con una partícula y calculemos

\[ \frac{d \vec{L}}{d t}=\frac{d}{d t}(m \vec{r} \times \vec{v})=m \frac{d \vec{r}}{d t} \times \vec{v}+m \vec{r} \times \frac{d \vec{v}}{d t} \label{eq:9.19} .\]

El primer término en el lado derecho va como\(\vec v \times \vec v\), que es cero. El segundo término puede ser reescrito como\(m \vec{r} \times \vec{a}\). Pero, según la segunda ley de Newton,\(m \vec a = \vec F_{net}\). Entonces, concluimos que

\[ \frac{d \vec{L}}{d t}=\vec{r} \times \vec{F}_{n e t} \label{eq:9.20} .\]

Entonces el momento angular, como el momento ordinario, se conservará si la fuerza neta sobre la partícula es cero, pero también, y esta es una diferencia importante, cuando la fuerza neta es paralela (o antiparalela) al vector de posición. Para el movimiento en un círculo con velocidad constante, esto es precisamente lo que sucede: la fuerza que actúa sobre la partícula es la fuerza centrípeta, que puede escribirse como\(\vec F_c = m \vec{a}_c = −m\omega^2 \vec r\) (usando la Ecuación (9.3.10)), así\(\vec{r} \times \vec{F}_{c}=0\), y el momento angular es constante.

La cantidad\(\vec{r} \times \vec{F}\) se llama el par de una fuerza alrededor de un punto (el origen a partir del cual\(\vec r\) se calcula, típicamente un punto de pivote o centro de rotación). Se denota con la letra griega\(\tau\), “tau”:

\[ \vec{\tau}=\vec{r} \times \vec{F} \label{eq:9.21} .\]

Para un objeto o sistema extendido, la velocidad de cambio del vector de momento angular estaría dada por la suma de los pares de todas las fuerzas que actúan sobre todas las partículas. Para cada par se necesita usar el vector de posición de la partícula sobre la que está actuando la fuerza. Como fue el caso al calcular la tasa de cambio del impulso ordinario de un sistema extendido (Sección 6.1), la tercera ley de Newton, con una pequeña suposición adicional, lleva a la cancelación de los pares debido a las fuerzas internas ³, y así nos quedamos con solo

\[ \vec{\tau}_{e x t, a l l}=\frac{d \vec{L}_{s y s}}{d t} \label{eq:9.22} .\]

No hace falta decir que todos los pares y momentos angulares necesitan ser calculados en relación con un mismo punto.

El par de una fuerza alrededor de un punto es básicamente una medida de cuán efectiva sería la fuerza para causar una rotación alrededor de ese punto. Ya que\(|\vec{r} \times \vec{F}|=r F \sin \theta\), se puede ver que depende de tres cosas: la magnitud de la fuerza, la distancia desde el centro de rotación hasta el punto donde se aplica la fuerza, y el ángulo en el que se aplica la fuerza. Todo esto se puede entender bastante bien en la figura\(\PageIndex{1}\) siguiente, especialmente si alguna vez has tenido que usar una llave para apretar o aflojar un perno:

Figura\(\PageIndex{1}\): El par alrededor del punto O de cada una de las fuerzas mostradas es una medida de lo efectivo que es para hacer que la varilla gire alrededor de ese punto.

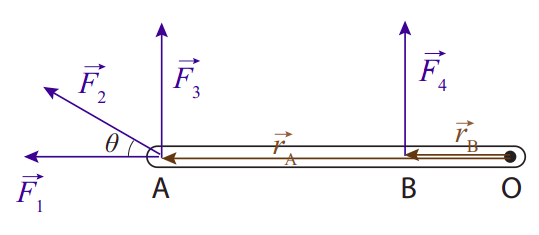
Claramente, la fuerza\(\vec F_1\) no provocará una rotación en absoluto, y en consecuencia su par es cero (ya que es paralelo a\(\vec r_A\)). Por otro lado, de todas las fuerzas mostradas, la más efectiva es\(\vec F_3\): se aplica la más alejada de O, para el mayor apalancamiento (nuevamente, piensa en tus experiencias con las llaves). También es perpendicular a la varilla, para un efecto máximo (\(\sin \theta\)= 1). La fuerza\(\vec F_2\), por el contrario, aunque también aplicada en el punto A se encuentra en desventaja debido al ángulo relativamente pequeño con el que hace\(\vec r_A\). Si te imaginas dividirlo en componentes, paralelos y perpendiculares a la varilla, solo el componente perpendicular (cuya magnitud es\(F_2 \sin \theta\)) sería efectivo para provocar una rotación; el otro componente, el paralelo a la varilla, se desperdiciaría, como\(\vec F_1\).

Para calcular los pares, entonces, básicamente necesitamos encontrar, por cada fuerza, el componente que es perpendicular al vector de posición de su punto de aplicación. Claramente, para ello ya no podemos representar un cuerpo extendido como un mero punto, como hicimos para los diagramas de cuerpo libre del Capítulo 6. Lo que necesitamos es un boceto más cuidadoso del objeto, solo lo suficientemente detallado como para que podamos decir a qué distancia del centro de rotación y en qué ángulo se aplica cada fuerza. Ese tipo de diagrama se llama diagrama de cuerpo libre extendido.

La figura\(\PageIndex{1}\) podría ser un ejemplo de un diagrama extendido de cuerpo libre, para un objeto sobre el que actúan cuatro fuerzas. Normalmente, sin embargo, en lugar de dibujar los vectores\(\vec r_A\) y solo\(\vec r_B\) indicaríamos sus longitudes en el diagrama (o tal vez incluso dejarlos fuera del todo, si no queremos sobrecargar el diagrama con detalle). Mostraré un par de ejemplos de diagramas extendidos de cuerpo libre en el siguiente par de secciones.

Como se indicó anteriormente, para calcular el par de torsión de cada fuerza que actúa sobre un objeto extendido se debe utilizar el vector\(\vec r\) de posición del punto donde se aplica la fuerza. Esto suele ser inequívoco para las fuerzas de contacto ⁴, pero ¿qué pasa con la gravedad? En principio, la fuerza de la gravedad actuaría sobre todas las partículas que componen el cuerpo, y tendríamos que sumar todos los pares correspondientes:

\[ \vec{\tau}^{G}=\vec{r}_{1} \times \vec{F}_{E, 1}^{G}+\vec{r}_{2} \times \vec{F}_{E, 2}^{G}+\ldots \label{eq:9.23} .\]

Podemos, sin embargo, simplificar esto sustancialmente al señalar que (cerca de la superficie de la Tierra, en cualquier caso), todas las fuerzas\(F_{E, 1}^{G}\),\(F_{E, 2}^{G}\)... apuntan en la misma dirección (es decir, hacia abajo), y todas son proporcionales a la masa de cada partícula. Si dejo que la masa total del objeto sea\(M\), y la fuerza total debida a la gravedad sobre el objeto sea\(\vec{F}_{E, o b j}^{G}\), entonces tengo\(\vec{F}_{E, 1}^{G}=m_{1} \vec{F}_{E, o b j}^{G} / M\),,...\(\vec{F}_{E, 2}^{G}=m_{2} \vec{F}_{E, o b j}^{G} / M\), y puedo reescribir la Ecuación (\ ref {eq:9.23}) como

\[ \vec{\tau}^{G}=\frac{m_{1} \vec{r}_{1}+m_{2} \vec{r}_{2}+\ldots}{M} \times \vec{F}_{E, o b j}^{G}=\vec{r}_{c m} \times \vec{F}_{E, o b j}^{G} \label{eq:9.24} \]

donde\(\vec r_{cm}\) es el vector de posición del centro de masa del objeto. Entonces, para encontrar el par debido a la gravedad sobre un objeto extendido, basta con tomar la fuerza total de gravedad sobre el objeto (es decir, el peso del objeto) a aplicar en su centro de masa. (Obviamente, entonces, el par de gravedad alrededor del centro de masa en sí será cero, pero en algunos casos importantes un objeto puede pivotar en un punto que no sea su centro de masa).

Volviendo a la Ecuación (\ ref {eq:9.22}), el mensaje principal de esta sección (otro, por supuesto, que la definición de par en sí), es que la tasa de cambio del momento angular de un objeto o sistema es igual al par neto debido a las fuerzas externas. De éste se siguen dos resultados especiales. Primero, si el par externo neto es cero, se conservará el momento angular, como fue el caso, en particular, para la colisión ilustrada anteriormente, en la Figura 9.2.3, entre una partícula y una varilla pivotada en un extremo. La única fuerza externa en ese caso fue la fuerza ejercida sobre la varilla, en el punto de pivote, por el propio pivote, pero el par de esa fuerza alrededor de ese punto es obviamente cero, ya que\(\vec r = 0\), por lo que nuestra suposición de que se conservó el momento angular total alrededor de ese punto era legítimo.

En segundo lugar, si se\(\vec L = I\vec \omega\) mantiene, y el momento de inercia\(I\) no cambia con el tiempo, podemos reescribir la Ecuación (\ ref {eq:9.22}) como

\[ \vec{\tau}_{\text {ext}, a l l}=I \vec{\alpha} \label{eq:9.25} \]

que es básicamente el equivalente rotacional de Newton, segunda ley,\(\vec F = m\vec a\). Utilizaremos esto extensamente en lo que resta de este capítulo.

Por último, señalar que las situaciones en las que el momento de inercia de un sistema\(I\),, cambia con el tiempo son relativamente fáciles de organizar para cualquier sistema deformable. Especialmente interesante es el caso cuando el par externo es cero, así\(L\) es constante, y un cambio en\(I\) por lo tanto provoca un cambio en\(\omega = L/I\): así es como, por ejemplo, una patinadora de hielo puede hacerse girar más rápido acercando sus brazos al eje de rotación (reduciéndola \(I\)), y, a la inversa, ralentizar su giro estirando los brazos. Esto se puede hacer incluso en ausencia de un punto de contacto con el suelo: los buzos de tabla alta, por ejemplo, también giran de esta manera cuando rizan sus cuerpos en una bola. Tenga en cuenta que, a lo largo de la inmersión, el momento angular del buceador alrededor de su centro de masa es constante, ya que la única fuerza que actúa sobre él (gravedad, descuidando la resistencia del aire) tiene un par cero alrededor de ese punto.

En todos los casos que acabamos de mencionar, el momento angular es constante, pero la energía cinética rotacional cambia. Esto se debe al trabajo realizado por las fuerzas internas (del cuerpo del patinador o del buceador), convirtiendo alguna energía interna (como la energía muscular elástica) en energía cinética rotacional, o viceversa. Una expresión conveniente para la energía cinética rotacional de un sistema cuando se\(\vec L = I\vec \omega\) sostiene es

\[ K_{r o t}=\frac{1}{2} I \omega^{2}=\frac{L^{2}}{I} \label{eq:9.26} \]

que muestra explícitamente cómo\(K\) cambiaría si se\(I\) cambiara y\(L\) permaneciera constante.

---

³ La suposición adicional es que la fuerza entre dos partículas cualesquiera se encuentra a lo largo de la línea que conecta las dos partículas (lo que significa que es paralela o antiparalela al vector\(\vec{r}_{1}-\vec{r}_{2}\)). En ese caso,\(\vec{r}_{1} \times \vec{F}_{12}+\vec{r}_{2} \times \vec{F}_{21}=\left(\vec{r}_{1}-\vec{r}_{2}\right) \times \vec{F}_{12}=0\). La mayoría de las fuerzas en la naturaleza satisfacen esta condición.

⁴ En realidad, las fuerzas de fricción y las fuerzas normales pueden “extenderse” sobre toda una superficie, pero, si el objeto tiene suficiente simetría, suele estar bien que “actúen” en el punto medio de esa superficie. Esto se puede probar a lo largo de las líneas de la derivación para la gravedad que sigue.