9.6: Movimiento rodante
- Page ID
- 128209
Como un paso adelante de un problema estático, podemos considerar una situación en la que la suma de las fuerzas externas es cero, así como la suma de los pares externos, sin embargo el sistema se mueve. A esto lo llamamos “moción no forzada”. La primera condición,\(\sum \vec{F}_{e x t}=0 \), significa que el centro de masa del sistema debe estar moviéndose con velocidad constante; la segunda condición significa que el momento angular total debe ser constante. Para un cuerpo rígido, esto significa que el tipo más general de movimiento no forzado puede describirse como una traslación del centro de masa con velocidad constante, acompañada de una rotación con velocidad angular constante alrededor del centro de masa. Para un sistema extendido y deformable, por otro lado, la presencia de fuerzas internas puede complicar mucho más el movimiento general. Basta pensar, por ejemplo, en el sistema solar: aunque todo gira en torno al sol, aunque todo gira en torno al sol, los movimientos de los planetas individuales y (especialmente) de las lunas pueden ser bastante complicados.
Un ejemplo simple de movimiento no forzado (para fines prácticos) es proporcionado por un objeto simétrico y rígido (como una bola o una rueda) que rueda sobre una superficie plana. Las fuerzas normales y de gravedad se cancelan entre sí, y como se encuentran a lo largo de la misma línea sus pares también se cancelan, por lo que ambas\(\vec v_{cm}\) y\(\vec L\) permanecen constantes. En principio, podrías imaginarte quitando el suelo y la gravedad y nada cambiaría: el mismo movimiento (en ausencia de resistencia al aire) simplemente continuaría para siempre.
En la práctica, hay disipación de energía asociada al movimiento rodante, principalmente porque, si el objeto rodante no es perfectamente rígido 6, entonces, a medida que rueda, diferentes partes del mismo se comprimen bajo la presión combinada de la gravedad y la fuerza normal, se expanden de nuevo, se comprimen de nuevo... Este tipo de “aplastamiento” constante termina convirtiendo la energía cinética macroscópica en energía térmica: es posible que hayas notado que las llantas de un automóvil se calientan mientras conduces, y también puedes estar familiarizado con el hecho de que obtienes un mejor kilometraje de gasolina (menos disipación de energía) cuando tus llantas están infladas al presión correcta que cuando son bajas (porque son más “rígidas”, menos deformables, en el primer caso).
Esta conversión de energía mecánica en energía térmica puede describirse formalmente introduciendo otra fuerza de “fricción” que llamamos la fuerza de fricción rodante. Eventualmente, la fricción rodante por sí sola pondría fin a cualquier objeto rodante, incluso en ausencia de resistencia al aire. Sin embargo, suele ser mucho más débil que la fricción deslizante, por lo que seguiremos ignorándola a partir de ahora. Es posible que ya hayas notado que normalmente un objeto puede rodar sobre una superficie mucho más lejos de lo que puede deslizarse sin rodar sobre la misma superficie. De hecho, lo que sucede a menudo es que, si intentas enviar el objeto (por ejemplo, una bola de billar) deslizándose, perderá energía cinética rápidamente ante la fuerza de la fricción cinética, pero también comenzará a girar bajo la influencia de la misma fuerza, hasta llegar a un punto crítico cuando la condición para rodar sin resbalar está satisfecho:
\[ | \vec v_{cm} | = R |\omega| \label{eq:9.34} .\]
En este punto, el objeto comenzará a rodar sin resbalar, y perdiendo velocidad a un ritmo mucho más lento.
El origen de la condición (\ ref {eq:9.34}) es bastante sencillo. Se puede imaginar un objeto que está rodando sin deslizarse como “midiendo la superficie” a medida que rueda (o viceversa, la superficie midiendo la circunferencia del objeto ya que sus diferentes puntos se presionan contra él en sucesión). Entonces, después de haber completado una revolución (\(2\pi\)radianes), debería haber literalmente “cubierto” una distancia en la superficie igual a\(2\pi R\), es decir, avanzada una distancia\(2\pi R\). Pero lo mismo tiene que ser cierto, proporcionalmente, para cualquier ángulo de rotación\(\Delta \theta\) otro que\(2\pi\): dado que la longitud del arco correspondiente es\(s = R|\Delta \theta|\), en una rotación sobre un ángulo\(|\Delta \theta|\) el centro de masa del objeto debe haber avanzado una distancia\(|\Delta x_{cm}| = s = R|\Delta \theta|\). Dividiendo por\(\Delta t\) como\(\Delta t \rightarrow 0\) entonces produce Ecuación (\ ref {eq:9.34}).
Obsérvese que, a diferencia de la Ecuación (8.4.12), a la que se parece mucho, la Ecuación (\ ref {eq:9.34}) no es una “identidad vectorial disfrazada”: no hay nada como la Ecuación (9.3.6) que pudiéramos sustituirla para que los signos salgan correctamente automáticamente. Simplemente debe tratarlo como una relación entre las magnitudes de\(\vec v_{cm}\) y\(\vec \omega \) y simplemente elegir los signos de manera apropiada para cada circunstancia, en función de su convención para direcciones positivas de traslación y rotación.
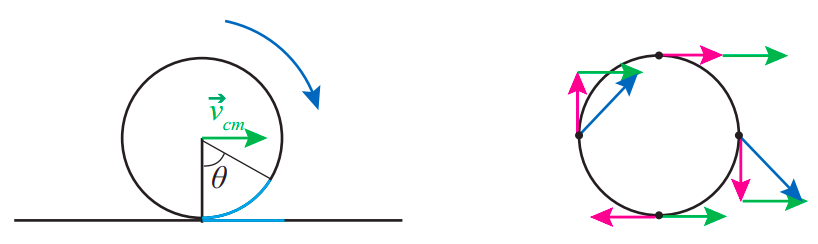
De hecho, podríamos usar la Ecuación (9.3.6) para encontrar la velocidad de cualquier punto del círculo, si vamos a un marco de referencia donde el centro está en reposo, es decir, el marco de referencia del centro de masa (CM); luego, para volver al marco de la Tierra, solo tenemos que agregar\(\vec v_{cm}\) (como vector) al vector que obtuvimos en el marco CM. En la figura se\(\PageIndex{1}\) muestra el resultado. Obsérvese, particularmente, que el punto en la parte inferior del círculo tiene una velocidad\(−R|\omega|\) en el marco CM, pero cuando volvemos al marco de la Tierra, su velocidad es\(−R|\omega| + v_{cm} = −R|\omega| + R|\omega| = 0\) (por la condición (\ ref {eq:9.34})). Así, siempre y cuando se mantenga la condición para rodar sin resbalar, el punto (o puntos) en el objeto rodante que están momentáneamente en contacto con la superficie tienen velocidad instantánea cero. Esto significa que, aunque hubiera una fuerza que actuara sobre el objeto en ese punto (como la fuerza de fricción estática), no funcionaría, ya que la potencia instantánea\(Fv\) para una fuerza aplicada allí siempre sería igual a cero.
En realidad no necesitamos la fuerza de fricción estática para mantener un objeto rodando sobre una superficie plana (como mencioné anteriormente, el movimiento podría en principio continuar “sin forzar” para siempre), pero las cosas son diferentes en un plano inclinado. La figura\(\PageIndex{2}\) muestra un objeto rodando por un plano inclinado, y el diagrama de cuerpo libre extendido correspondiente.
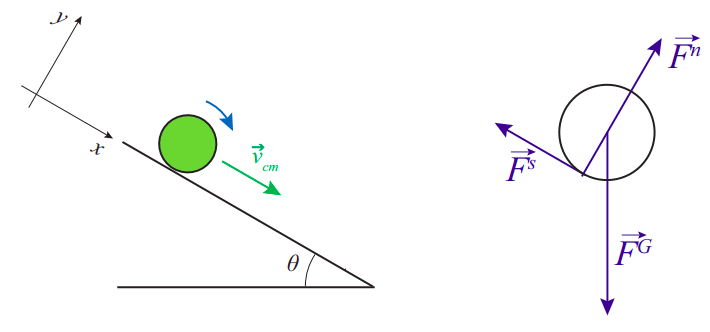
Las ecuaciones básicas que utilizamos para resolver para el movimiento del objeto son la ecuación de suma de fuerzas:
\[ \sum \vec{F}_{e x t}=M \vec{a}_{c m} \label{eq:9.35} \]
la ecuación de par neto, con pares tomados alrededor del centro de masa 7
\[ \sum \vec{\tau}_{e x t}=I \vec{\alpha} \label{eq:9.36} \]
y la extensión de la condición de balanceo sin deslizamiento, (\ ref {eq:9.34}), a las aceleraciones:
\[ \left|a_{c m}\right|=R|\alpha| \label{eq:9.37}.\]
Para la situación que se muestra en la Figura\(\PageIndex{2}\), si bajamos el plano como la dirección positiva para el movimiento lineal, y los pares en sentido horario como negativos, tenemos que escribir\(a_{cm} = −R\alpha\). En la dirección perpendicular al plano, concluimos de (\ ref {eq:9.35}) que\(F^n = Mg \cos \theta\), una ecuación que en realidad no necesitaremos 8; en la dirección a lo largo del plano, tenemos
\[ M a_{c m}=M g \sin \theta-F^{s} \label{eq:9.38} \]
y la ecuación de par solo da\(−F^sR = I\alpha\), que con\(a_{cm} = −R\alpha\) se convierte
\[ F^{s} R=I \frac{a_{c m}}{R} \label{eq:9.39} .\]
Podemos eliminar\(F^s\) entre estas dos ecuaciones y resolver por\(a_{cm}\):
\[ a_{c m}=\frac{g \sin \theta}{1+I /\left(M R^{2}\right)} \label{eq:9.40} .\]
Ahora se puede ver por qué, a principios de semestre, siempre tuvimos cuidado de asumir que todos los objetos que enviamos abajo planos inclinados estaban deslizando, ¡no rodando! La aceleración para un objeto rodante nunca es igual a simple\(g \sin \theta\). Lo más notable es que el factor de corrección depende únicamente de la forma del objeto rodante, y no de su masa o tamaño, ya que la relación de\(I\) a\(MR^2\) es independiente de\(m\) y\(R\) para cualquier geometría dada. Así, por ejemplo, para un disco,\(I = \frac{1}{2}MR^2\), así\(a_{cm} = \frac{2}{3} g \sin \theta\), mientras que para un aro,\(I = MR^2\), así\(a_{cm} = \frac{1}{2} g \sin \theta\). Por lo que cualquier disco o cilindro sólido siempre rodará por la pendiente más rápido que cualquier aro o cilindro hueco, independientemente de la masa o tamaño.
Este resultado bastante sorprendente puede entenderse mejor en términos de energía. Primero, permítanme mostrar (resultado que está algo atrasado) que para un objeto rígido que está girando alrededor de un eje que pasa por su centro de masa con velocidad angular\(\omega\) podemos escribir la energía cinética total como
\[ K=K_{c m}+K_{r o t}=\frac{1}{2} M v_{c m}^{2}+\frac{1}{2} I \omega^{2} \label{eq:9.41} .\]
Esto se debe a que para cada partícula la velocidad se puede escribir como\(\vec{v}=\vec{v}_{c m}+\vec{v}^{\prime}\), donde\(\vec{v}^{\prime}\) está la velocidad relativa al centro de masa (es decir, en el marco CM). Ya que en este fotograma el movimiento es una simple rotación, tenemos\( \left|v^{\prime}\right|=\omega r \), donde\(r\) está la distancia de la partícula al eje. Por lo tanto, la energía cinética de esa partícula será
\ begin {align}
\ frac {1} {2} m v^ {2} =\ frac {1} {2}\ vec {v}\ cdot\ vec {v} &=\ frac {1} {2} m\ izquierda (\ vec {v} _ {c m} +\ vec {v} ^ {\ prime}\ derecha)\ cdot\ izquierda (\ vec {v} +\ vec {v} ^ {\ prime}\ derecha)\ cdot\ izquierda (\ vec {v} c {v} _ {c m} +\ vec {v} ^ {\ prime}\ derecha)\ nonumber\\
&=\ frac {1} {2} m v_ {c m} ^ {2} +\ frac {1} {2} m v^ {\ prime 2} +m\ vec {v} _ _ {c m}\ cdot\ vec {v} ^ ^\ prime}\ nonumber\\
&=\ frac {1} {2} m v_ {c m} ^ {2} +\ frac {1} {2} m r^ {2}\ omega^ {2} +\ vec {v} _ _ {c m}\ cdot\ vec {p} ^ {\ prime}\ label {eq:9.42}
\ end {align}
(Observe cómo he hecho uso del producto punto para calcular la magnitud al cuadrado de un vector.) En la última línea, la cantidad\(\vec{p}^{\prime}\) es el impulso de esa partícula en el marco CM. Agregar esos momentos para todas las partículas debería dar cero, ya que, como vimos en un capítulo anterior, el marco del centro de masa es el marco de impulso cero. Luego, sumando las contribuciones de todas las partículas al primer y segundo términos en\ ref {eq:9.42} da Ecuación (\ ref {eq:9.41}).
Volviendo a nuestro cuerpo rodante, usando la Ecuación (\ ref {eq:9.41}) y la condición de rodar sin resbalar (\ ref {eq:9.34}), vemos que la relación de la energía cinética traslacional a la rotacional es
\[ \frac{K_{c m}}{K_{r o t}}=\frac{m v_{c m}^{2}}{I \omega^{2}}=\frac{m R^{2}}{I} \label{eq:9.43} .\]
La cantidad de energía disponible para acelerar el objeto inicialmente es solo la energía potencial gravitacional del sistema objeto-tierra, y que tiene que dividirse entre traslacional y rotacional en la proporción (\ ref {eq:9.43}). Un objeto con un tamaño proporcionalmente mayor\(I\) es aquel que, para una velocidad angular dada, necesita más energía cinética rotacional, porque más de su masa está alejada del eje de rotación. Esto deja menos energía disponible para su movimiento de traslación.
Recursos
Desafortunadamente, realmente no tendremos tiempo suficiente este semestre para explorar más a fondo los muchos efectos interesantes que se derivan de la naturaleza vectorial de la Ecuación (9.4.2), pero al menos estás inconscientemente familiarizado con algunos de ellos si alguna vez has aprendido a andar en bicicleta! Algunas referencias interesantes de Internet (¡algunas de las cuales quizás podrían inspirar un buen proyecto de Honors!) son los siguientes:
- Conferencia de Walter Lewin sobre movimiento giroscópico (y movimiento rodante):
https://www.youtube.com/watch?v=N92FYHHT1qM - Un video de “Veritasium” sobre “antigravedad”:
https://www.youtube.com/watch?v=GeyDf4ooPdo
https://www.youtube.com/watch?v=tLMpdBjA2SU - Y el viejo truco de poner un giroscopio (volante) en una maleta:
https://www.youtube.com/watch?v=zdN6zhZSJKw
Si alguno de los enlaces anteriores está muerto, intenta buscarlos en Google. (¡Es posible que también quieras avisarme!)
6 Existe un argumento sencillo, basado en la teoría de la relatividad de Einstein, que muestra que un objeto infinitamente rígido no puede existir: si lo hiciera, podrías enviar una señal instantáneamente de un extremo al otro, simplemente empujando o tirando de tu extremo. En la práctica, dicho movimiento no puede llegar al otro extremo más rápido que la velocidad de una onda sonora (es decir, una onda de compresión) en el material. Estudiaremos tales ondas (lo que implica que el medio no es infinitamente rígido) en el Capítulo 12.
7 Es posible que te sientas un poco inquieto por el hecho de que el marco CM es ahora un marco acelerado, y por lo tanto no inercial. ¿Cómo sabemos que la Ecuación (\ ref {eq:9.36}) incluso se aplica ahí? Esto es, en efecto, un punto no trivial. Sin embargo, como veremos en un capítulo posterior, estar en un marco de referencia uniformemente acelerado equivale a estar en un campo gravitacional uniforme, y acabamos de demostrar que, para todos los fines relacionados con el par, se puede tratar dicho campo como una sola fuerza aplicada al centro de masa de un objeto. Tal fuerza (o “pseudofuerza” en este caso) claramente no contribuye al par alrededor del centro de masa, por lo que la Ecuación (\ ref {eq:9.36}) se aplica en el marco CM.
8 A menos que estuviéramos tratando de responder a una pregunta como “¿qué tan empinado tiene que ser el avión para rodar sin resbalar para volverse imposible?”


