10.1: La Ley de Cuadrados Inversales
- Page ID
- 128297
Hasta este punto, todo lo que les he dicho sobre la gravedad es que, cerca de la superficie de la Tierra, la fuerza gravitacional ejercida por la Tierra sobre un objeto de masa\(m\) es\(F^G = mg\). Esta es, efectivamente, una aproximación bastante buena, pero realmente no te dice nada sobre cuál es la fuerza gravitacional donde están involucrados otros objetos o distancias.
La primera teoría integral de la gravedad, formulada por Isaac Newton a finales del siglo XVII, postula que cualesquiera dos “partículas” con masas\(m_1\) y\(m_2\) ejercerán una fuerza atractiva (un “tirón”) entre sí, cuya magnitud es proporcional al producto de las masas, y inversamente proporcional al cuadrado de la distancia entre ellos. Matemáticamente, escribimos
\ [F_ {12} ^ {G} =\ frac {G m_ {1} m_ {2}} {r_ {12} ^ {2}}\ etiqueta {eq:10.1}.\]
Aquí,\(r_{12}\) es solo la magnitud del vector de posición de la partícula 2 con relación a la partícula 1 (así \(r_{12}\) es, de hecho, la distancia entre las dos partículas), y \(G\) es una constante, conocida como “constante de Newton” o la constante gravitacional, que en el momento de Newton aún no se había determinado experimentalmente. Se puede ver en la Ecuación (\ ref {eq:10.1}) que\(G\) es simplemente la magnitud, en newtons, de la fuerza de atracción entre dos masas de 1 kg a una distancia de 1 m de distancia. Esto resulta tener el valor ridículamente pequeño\(G\) = 6.674×10 −11 N m 2 /kg 2 (o, como se escribe más comúnmente, m 3 kg −1 s −2). Fue medido por primera vez por Henry Cavendish en 1798, en lo que fue, sin duda, un tour de force experimental para esa época (más sobre eso más adelante, pero puedes echar un vistazo a la sección “Temas Avanzados” del siguiente capítulo si ya tienes curiosidad). Como puedes ver, la gravedad como fuerza entre dos objetos ordinarios cualquiera es absolutamente insignificante, y toma la masa de un planeta para convertirlo en algo que puedas sentir.
La ecuación (\ ref {eq:10.1}), como se afirma, se aplica a las partículas, es decir, en la práctica, a cualquier objeto que sea muy pequeño en comparación con la distancia entre ellas. La fuerza neta entre masas extendidas se puede obtener usando cálculo, rompiendo los dos objetos en trozos muy pequeños y agregando (¡vectorialmente!) la fuerza ejercida por cada pequeña parte de un objeto sobre cada pequeña parte del otro objeto. Esto requiere el uso de cálculo integral a un nivel bastante avanzado, y para objetos de forma irregular solo se pueden computar numéricamente. Para los objetos esféricamente simétricos, sin embargo, resulta que el resultado (\ ref {eq:10.1}) aún se mantiene exactamente, siempre que la cantidad \(r_{12}\) se tome como la distancia entre el centro de las esferas. El mismo resultado también es válido para la fuerza entre una esfera de tamaño finito y una “partícula”, nuevamente con la distancia a la partícula medida desde el centro de la esfera.
Para el resto de este capítulo, simplemente asumiremos que la Ecuación (\ ref {eq:10.1}) es una buena aproximación para ser utilizada en cualquiera de los problemas que encontraremos involucrando objetos extendidos. Se puede estimar visualmente lo bueno que puede ser, por ejemplo, cuando se aplica al sistema Tierra-Luna (como lo haremos en un momento), a partir de una mirada a la Figura a\(\PageIndex{1}\) continuación:
Figura\(\PageIndex{1}\): La luna, la tierra, y la distancia entre ellas, todas aproximadamente a escala.
Con base en esta imagen parece que podría estar bien tratar a la luna como una “partícula”, pero que no haría, en general, descuidar el radio de la Tierra; es decir, deberíamos usar para\(r_{12}\) la distancia de la luna al centro de la Tierra, no sólo a su superficie.
Antes de llegar allí, sin embargo, empecemos más cerca de casa y veamos qué sucede si tratamos de usar la Ecuación (\ ref {eq:10.1}) para calcular la fuerza ejercida por la Tierra sobre un objeto si es masa\(m\) cerca de su superficie, digamos, a una altura\(h\) sobre el suelo. Claramente, si el radio de la Tierra es\(R_E\), la distancia del objeto al centro de la Tierra es\(R_E + h\), y esto es para lo que deberíamos usar\(r_{12}\) en la Ecuación (\ ref {eq:10.1}). No obstante, al señalar que el radio de la Tierra es de unos 6,000 km (más precisamente,\(R_E\) = 6.37×10 6 m), y el pico de montaña más alto está a solo unos 9 km sobre el nivel del mar, se puede ver que casi siempre será una muy buena aproximación para establecer\(r_{12}\) igual a justo \(R_E\), lo que resulta en una fuerza
\ [F_ {E, o} ^ {G}\ simeq\ frac {G M_ {E} m} {R_ {E} ^ {2}} =m\ frac {6.674\ veces 10^ {-11}\:\ mathrm {m} ^ {3} \ mathrm {kg} ^ {-1}\ mathrm {s} ^ {-2}\ veces 5.97 veces 10^ {24}\: \ mathrm {kg}} {\ izquierda (6.37\ veces 10^ {6}\:\ mathrm {m}\ derecha) ^ {2}} =m \ veces 9.82\:\ frac {\ mathrm {m}} {\ mathrm {s} ^ {2}} \ label {eq:10.2} \]
donde he usado el valor actualmente conocido\(M_E\) = 5.97 × 10 24 kg para la masa de la Tierra. Como puede ver, recuperamos el resultado familiar\(F^G = mg\), con\(g \simeq\) 9.8 m/s 2, que hemos estado usando todo el semestre. Podemos reescribir este resultado (cancelando la masa \(m\)) en el formulario
\ [g_ {E} =\ frac {G M_ {E}} {R_ {E} ^ {2}} \ etiqueta {eq:10.3}.\]
Aquí he puesto un subíndice\(E\) \(g\) para enfatizar que esta es la aceleración de la gravedad cerca de la superficie de la Tierra, y que la misma fórmula podría usarse para encontrar la aceleración de la gravedad cerca de la superficie de cualquier otro planeta o luna, solo reemplazando\(M_E\) y \(R_E\)por la masa y el radio del planeta o luna en cuestión. Así, podríamos hablar de\(g_{moon}\),\(g_{Mars}\), etc., y en algunos problemas de tareas se le pedirá que calcule estas cantidades. Claramente, además de decirte qué tan rápido caen las cosas en un planeta dado, la cantidad te\(g_{planet}\) permite averiguar cuánto pesaría algo en la superficie de ese planeta (simplemente multiplicar\(g_{planet}\) por la masa del objeto); alternativamente, la proporción de \(g_{planet}\) a\(g_E\) será la relación entre el peso del objeto en ese planeta y su peso aquí en la Tierra.
Por supuesto, históricamente, esto no es lo que Newton y sus contemporáneos habrían hecho: tenían medidas de objetos en caída libre (o deslizándose sobre planos inclinados) que les hubieran dado el valor de\(g\), e incluso tenían una idea bastante buena del radio de la Tierra 1 , pero no conocían\(G\) ni la masa de la Tierra, así que todo lo que podían obtener de la Ecuación (\ ref {eq:10.3}) era el valor del producto\(GM_E\). Fue solo un siglo después, cuando Cavendish midió\(G\), que pudieron obtener de eso la masa de la tierra (¡como resultado de lo cual, se le dio a conocer como “el hombre que pesaba la tierra”!)
Lo que Newton podía hacer, sin embargo, con solo este conocimiento del valor de\(GM_E\), era algo que, para su época, era aún más dramático y de gran alcance: a saber, podría “probar” su intuición de que la misma interacción fundamental —la gravedad— que hace que una manzana caiga cerca de la superficie de la Tierra, llegando a cientos de miles de kilómetros de distancia hacia el espacio, también proporciona la fuerza necesaria para mantener a la luna en su órbita. Esto reunió la ciencia (física) con destino a la Tierra y la ciencia “celestial” (astronomía) de una manera que nadie había soñado antes.
Para ver cómo funciona esto, comencemos asumiendo que la luna sí se mueve en círculo, con la Tierra inmóvil en el centro (todas estas son aproximaciones, como veremos más adelante, pero dan el orden correcto de magnitud al final, que es todo lo que Newton podría haber esperado de todos modos). La fuerza \(F^G_{E,m}\) entonces tiene que proporcionar la fuerza centrípeta\ (F_c = M_ {luna}\ omega^2r_ {e, m}\), donde\(\omega\) está la velocidad angular de la luna. Podemos cancelar la masa de la luna de ambos términos y escribir esta condición como
\ [\ frac {G M_ {E}} {r_ {e, m} ^ {2}} =\ omega^ {2} r_ {e, m}\ etiqueta {eq:10.4}.\]
La luna gira alrededor de la tierra una vez aproximadamente cada 29 días, lo que es de aproximadamente 29 × 24 × 3600 = 2.5 × 10 6 s. Así\(\omega\) es\(2\pi\) radianes por 2.5 millones de segundos, o\(\omega\) = 2.5 × 10 −6 rad/s. Sustituyendo esto en Ecuación (\ ref {eq:10.4}), así como la resultado\(GM_E = gR^2_E\) (tenga en cuenta que, como se indicó anteriormente, no necesitamos saber\(G\) y\(M_E\) por separado), obtenemos\(r_{e,m}\) = 3.99 × 10 8 m, bastante cerca del valor aceptado hoy de la distancia promedio Tierra-Luna, que es de 3.84 × 10 8 km. Newton no habría sabido\(r_{e,m}\) con tanta precisión, pero aún así habría tenido una idea bastante buena de que este era, de hecho, el orden correcto de magnitud 2.
1 El radio de la tierra se conocía, al menos aproximadamente, desde la antigüedad. Los griegos lo resolvieron por primera vez observando la forma en que los objetos altos desaparecen bajo el horizonte cuando se ven desde un barco en el mar. La próxima vez que alguien intente decirte que la gente solía creer que la tierra era plana, ¡pregúntales exactamente de qué “gente” están hablando!
2 Y, sí, ¡las primeras estimaciones de la distancia entre la tierra y la luna también se remontan a los antiguos griegos! Puedes averiguarlo, si conoces el radio de la tierra, observando cuánto tiempo tarda la luna en transitar por la sombra de la tierra durante un eclipse lunar.
Energía Potencial Gravitacional
Desde que introduje el concepto de energía potencial en el Capítulo 5, he estado utilizando\(U^G = mgy\) para la energía potencial gravitacional del sistema formado por la Tierra y un objeto de masa a\(m\) una altura\(y\) sobre la superficie de la Tierra. Esto funciona bien siempre y cuando la fuerza de gravedad sea aproximadamente constante, es decir, siempre y cuando\(y\) sea mucho menor que el radio de la tierra, pero obviamente debe descomponerse en algún momento.
Recordemos que, si la interacción entre dos objetos puede ser descrita por una función de energía potencial de las coordenadas de los objetos\(U(x_1, x_2)\), entonces (en una dimensión) la fuerza ejercida por el objeto 1 sobre el objeto 2 podría escribirse como\ (F_ {12} = −du/dx_2\). Como la fuerza de gravedad sí se encuentra a lo largo de la línea que une las dos partículas, podemos hacer trampa un poco y tratarlo como un problema unidimensional, con\ ((F^G _ {12}) _x = −gm_1m_2/ (x_1 − x_2) ^2\) (He puesto un signo menos ahí bajo el supuesto de que la partícula 1 está a la izquierda de la partícula 2, es decir,\ (x _1 < x_2\), y la fuerza en 2 está a la izquierda), y encontrar una función de energía potencial cuya derivada da eso. La respuesta es claramente
\ [U^ {G}\ izquierda (x_ {1}, x_ {2}\ derecha) =-\ frac {G m_ {1} m_ {2}} {x_ {2} -x_ {1}} +C\ etiqueta {eq:10.5} \]
donde\(C\) es una constante arbitraria. (Por favor, tómese un momento para verificar por sí mismo eso \(−dU^G/dx_2 = −(F^G_{12})_x\), de hecho,, y también\ (−du^g/dx_1 = − (F^G_ {21}) _x\).)
Desde que he asumido\(x_2 > x_1\), el denominador en la Ecuación (\ ref {eq:10.5}) es solo la distancia entre las dos partículas, y la función de energía potencial podría escribirse, en tres dimensiones, como
\ [U^ {G}\ izquierda (r_ {12}\ derecha) =-\ frac {G m_ {1} m_ {2}} {r_ {12}} \ label {eq:10.6}\]
donde\ ( r_ {12} =\ izquierda|\ vec {r} _ {2} -\ vec {r} _ {1}\ derecha|\), y he establecido la constante\(C\) igual a cero. Esto quiere decir que la energía potencial del sistema siempre es negativa, lo que es, a primera vista, un resultado extraño. Sin embargo, no hay forma de elegir la constante\(C\) en (\ ref {eq:10.5}) que impida que: no importa cuán grande y positiva\(C\) pueda ser, el primer término en (\ ref {eq:10.5}) siempre puede llegar a ser más grande (en magnitud) y negativo, si las partículas están muy juntas. Entonces bien podríamos elegir\(C\) = 0, lo que, al menos, nos da el resultado un tanto reconfortante de que la energía potencial del sistema es cero cuando las partículas están “infinitamente” distantes entre sí, es decir, tan separadas que ya no sienten una fuerza la una de la otra.
Pero la Ecuación (\ ref {eq:10.5}) también tiene sentido de una manera diferente: es decir, muestra que la energía potencial del sistema aumenta a medida que las partículas se separan más. En efecto, esperamos, físicamente, que si separas las partículas por una gran distancia y luego las sueltas, capten mucha velocidad a medida que se acerquen entre sí; o, dicho de otra manera, que la fuerza que realiza el trabajo sobre una gran distancia les dé una gran cantidad de energía cinética, que debe provienen de la energía potencial del sistema. Pero, de hecho, matemáticamente, la Ecuación (\ ref {eq:10.6}) concuerda con esta expectativa: para cualquier distancia finita,\(U^G\) es negativa, y se hace menor en magnitud a medida que aumenta la distancia, lo que significa que aumenta algebraicamente (ya que un número como, digamos, −0.1 es, de hecho, mayor que un número como −10). Entonces, a medida que las partículas se separan cada vez más, la energía potencial del sistema aumenta, ¡hasta un valor máximo de cero!
Aún así, aunque tenga sentido matemáticamente, la noción de una “energía negativa” es difícil de entender. Sólo te puedo ofrecer dos formas posibles de mirarlo. Una es simplemente no pensar en la energía potencial como algo así como una “sustancia”, sino solo un dispositivo de contabilidad que usamos para hacer un seguimiento del potencial que un sistema tiene que hacer funcionar para nosotros, o (más o menos equivalentemente) para darnos energía cinética, que siempre es positiva y por lo tanto puede ser pensada como la energía “real”. Desde este punto de vista, no importa si\(U\) es positivo o negativo: lo único que importa es el cambio\(\Delta U\), y si este cambio tiene un signo que tiene sentido. Esto, al menos, es el caso aquí, como he argumentado en el párrafo anterior.
La otra perspectiva es casi opuesta, y se basa en la teoría de la relatividad de Einstein: en esta teoría, la energía total de un sistema es efectivamente “algo así como una sustancia”, en el sentido de que está directamente relacionada con la inercia total del sistema,\(m\), a través de la famosa ecuación\(E = mc^2\). Desde este punto de vista, la energía total de un sistema de dos partículas, que interactúan gravitacionalmente, en reposo y separadas por una distancia \(r_{12}\), sería la suma de la energía potencial gravitacional (negativa), y las “energías de descanso” de las dos partículas,\(m_1c^2\) y \(m_2c^2\):
\ [E_ {\ texto {total}} =m_ {1} c^ {2} +m_ {2} c^ {2} -\ frac {G m_ {1} m_ {2}} {r_ {12}}\ label {eq:10.7} \]
y esta cantidad siempre será positiva, a menos que una de las “partículas” sea un agujero negro y la otra esté dentro de ella 3!
Tenga en cuenta que no vamos a utilizar la ecuación (\ ref {eq:10.7}) este semestre en absoluto, ya que aquí solo nos preocupa la mecánica no relativista. Es decir, no incluiremos en absoluto la “energía de descanso” en nuestros cálculos de la energía total de un sistema. No obstante, si lo hiciéramos, encontraríamos que un sistema cuya energía de reposo viene dada por la Ecuación (\ ref {eq:10.7}) tiene, de hecho, una inercia que es menor que la suma \(m_1 + m_2\). Esto sugiere fuertemente que la negatividad de la energía potencial no es solo una conveniencia matemática, sino que refleja un hecho físico fundamental.
Para un sistema de más de dos partículas, la energía potencial gravitacional total se obtendría agregando expresiones como (\ ref {eq:10.6}) sobre todos los pares de partículas. Así, por ejemplo, para tres partículas una tendría
\ [U^ {G}\ izquierda (\ vec {r} _ {1}, \ vec {r} _ {2},\ vec {r} _ {3}\ derecha) =-\ frac {G m_ {1} m_ {2}} {r_ {12}} -\ frac {G m_ {1} m_ {3}} {r_ {13} -\ frac {G m_ {2} m_ {3}} {r_ {23}}\ etiqueta {eq:10.8}.\]
Una masa grande como la tierra, o una estrella, tiene una cantidad intrínseca de energía potencial gravitacional que se puede calcular dividiéndola en pequeñas partes y realizando una suma como (\ ref {eq:10.8}) sobre todos los pares posibles de “partes”. (Como es habitual, esta suma suele evaluarse como una integral, tomando el límite de un número infinito de partes infinitesimalmente pequeñas). Esta “autoenergía” no cambia con el tiempo, y por lo tanto no necesita ser incluida en la mayoría de los cálculos de energía que involucran fuerzas gravitacionales entre objetos extendidos.
Una cosa que quizás te estés preguntando, respecto a la Ecuación (\ ref {eq:10.6}) para la energía potencial de un par de partículas (o, para el caso, Ecuación (\ ref {eq:10.1}) para la fuerza), es lo que sucede cuando la distancia\(r_{12}\) va a cero, ya que la expresión matemática parece llegar a ser infinito. Esto es técnicamente cierto, pero, en la práctica, solo sería un problema para un par de partículas puntuales verdaderas, objetos que literalmente serían puntos matemáticos, sin dimensiones en absoluto. Tales cosas pueden existir en algún sentido —los electrones pueden ser un ejemplo— pero necesitan ser descritas por la mecánica cuántica, que es una teoría matemática completamente diferente.
Para objetos de tamaño finito, no se puede seguir usando una ecuación como (\ ref {eq:10.6}) (o (\ ref {eq:10.1}), para la fuerza) cuando se encuentra bajo la superficie del objeto. Si pudieras cavar un túnel hasta el centro de una hipotética “tierra” que tuviera una densidad constante, la energía potencial del sistema formado por esta “tierra” y una partícula de masa\(m\), a una\(r\) distancia del centro, se vería como se muestra en la Figura\(\PageIndex{2}\). Observe cómo \(U^G\) se vuelve “plano”, indicando una posición de equilibrio (fuerza cero), como\(r \rightarrow 0\). Es lógico que la fuerza gravitacional neta en el centro de este modelo “tierra” sea cero, ya que una sería tirada igualmente fuerte en todas las direcciones por toda la masa alrededor.
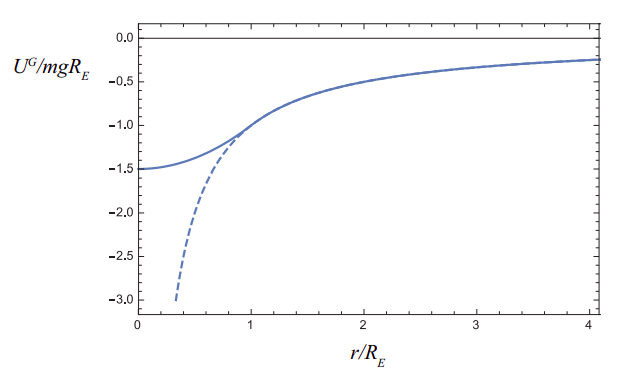
Figura \(\PageIndex{2}\): Energía potencial gravitacional de un sistema formado por una partícula de masa\(m\) y una tierra hipotética con densidad uniforme, una masa\(M\) y un radio\(R_E\), en función de la distancia\(r\) entre la partícula y el centro de la “tierra” ( línea continua). La línea discontinua muestra el resultado para un sistema de dos partículas (puntiformes). La energía\(U^G\) se expresa en unidades de\(mgR_E\), donde\(g = GM/R^2_E\).
Finalmente, déjame mostrarte que el resultado (\ ref {eq:10.6}) es totalmente consistente con la aproximación \(U^G = mgy\) que hemos estado usando hasta ahora cerca de la superficie de la tierra. (Si no te interesan las derivaciones matemáticas, no dudes en saltarte este siguiente bit). Consideremos una partícula de masa m que inicialmente se encuentra en la superficie de la tierra, y luego la movemos a una altura\(h\) por encima de la tierra. El cambio en la energía potencial, según (\ ref {eq:10.6}), es
\ [U_ {f} ^ {G} -U_ {i} ^ {G} =-\ frac {G M_ {E} m} {R_ {E} +h} +\ frac {G M_ {E} m} {R_ {E}}\ etiqueta {eq:10.9}.\]
Si escribimos ambos términos con un denominador común, obtenemos
\ [U_ {f} ^ {G} -U_ {i} ^ {G} =\ frac {G M_ {E} m} {\ izquierda (R_ {E} +h\ derecha) R_ {E}} h\ simeq\ frac {G M_ {E} m} {R_ {E} ^ {2}} h=m g h\ etiqueta {eq:10.10}.\]
La única aproximación aquí ha sido establecer\( R_{E}+h \simeq R_{E} \) en el denominador de esta expresión. Dado que\(R_E\) es del orden de miles de kilómetros, esta es una excelente aproximación, siempre y cuando\(h\) sea menor que, digamos, unos pocos cientos de metros.
3 Para una justificación de esta afirmación, consúltese la definición del radio Schwarzschild, más adelante en este capítulo.
Tipos de órbitas bajo una fuerza de cuadrado inverso
Considera un sistema formado por dos partículas (o dos esferas perfectas y rígidas) que interactúan solo entre sí, a través de su atracción gravitacional. La conservación del impulso total nos dice que el centro de masa del sistema está ya sea en reposo o moviéndose a velocidad constante. Supongamos que uno de los objetos tiene una masa mucho mayor,\(M\), que el otro, de manera que, a efectos prácticos, su centro coincide con el centro de masa de todo el sistema. Esta no es una mala aproximación si lo que nos interesa es, por ejemplo, la órbita de un planeta alrededor del sol. El planeta más masivo, Júpiter, solo tiene alrededor de 0.001 veces la masa del sol.
En consecuencia, asumiremos que el objeto más masivo no se mueve en absoluto (al trabajar en su marco de referencia del centro de masa, si es necesario, tenga en cuenta que, según nuestros supuestos, este será un marco de referencia inercial a una buena aproximación), y nos ocuparemos únicamente del movimiento del objeto menos masivo bajo la fuerza\(F = GMm/r^2\), donde \(r\) está la distancia entre los centros de los dos objetos. Dado que esta fuerza siempre está tirando hacia el centro del objeto más masivo (es lo que a menudo se llama una fuerza central), su par alrededor de ese punto es cero, y por lo tanto el momento angular\(\vec L\),, del cuerpo menos masivo alrededor del centro de masa del sistema es constante. Este es un resultado interesante: nos dice, por ejemplo, que el movimiento está confinado a un plano, el mismo plano que los vectores \(\vec r\) y\(\vec v\) definieron inicialmente, ya que su producto cruzado no puede cambiar.
A pesar de esta simplificación, el cálculo de la trayectoria del objeto, u órbita, requiere algunas técnicas matemáticas bastante avanzadas, salvo en el caso más simple, que es el de una órbita circular de radio\(R\). Tenga en cuenta que este caso requiere una relación muy precisa para mantener entre la velocidad del objeto y el radio de la órbita, que podemos obtener estableciendo la fuerza de gravedad igual a la fuerza centrípeta:
\ [\ frac {G M m} {R^ {2}} =\ frac {m v^ {2}} {R} \ etiqueta {eq:10.11}.\]
Entonces, si queremos, digamos, poner un satélite en órbita circular alrededor de un cuerpo central de masa\(M\) y a una \(R\) distancia del centro de ese cuerpo, podemos hacerlo, pero solo siempre que le demos al satélite una velocidad inicial\ (v=\ sqrt {G M/ R}\) en una dirección perpendicular a la radio. Pero, ¿y si liberáramos el satélite a la misma distancia\(R\), pero con una velocidad diferente, ya sea en magnitud o dirección? Demasiada velocidad lo alejaría del círculo, por lo que la distancia al centro,\(r\), aumentaría temporalmente; esto aumentaría la energía potencial del sistema y en consecuencia reduciría la velocidad del satélite, por lo que eventualmente se retiraría; luego volvería a acelerar, y así sucesivamente.
Puedes experimentar con este tipo de cosas tú mismo usando la demostración PhET en este enlace:
https://phet.colorado.edu/en/simulation/gravity-and-orbits
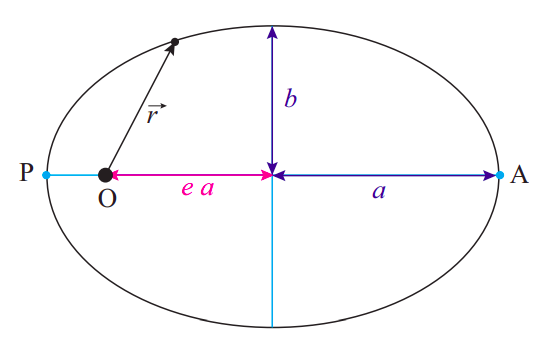
Encontrarás que, siempre y cuando no le des al satélite —o al planeta, en la simulación— demasiada velocidad (¡más sobre esto más adelante!) la órbita que obtienes es, de hecho, una curva cerrada, el tipo de curva que llamamos elipse. He dibujado una de esas elipse para ti en Figura\(\PageIndex{3}\).
Figura\(\PageIndex{3}\): Una órbita elíptica. El eje semimañor es\(a\), el eje semiminor es\(b\), y la excentricidad\(e=\sqrt{1-b^{2} / a^{2}}\) = 0.745 en este caso. El “centro de atracción” (el sol, por ejemplo, en el caso de la órbita de un planeta o cometa) se encuentra en el punto O.
Como curva geométrica, cualquier elipse puede caracterizarse por un par de números,\(a\) y\(b\), que son las longitudes de los ejes semimajor y semiminor, respectivamente. Estas longitudes se muestran en la figura. Alternativamente, se podría especificar\(a\) y un parámetro conocido como la excentricidad, denotado por\(e\) (¡no confundas este “\(e\)” con el coeficiente de restitución del Capítulo 4!) , que es igual a\(e=\sqrt{1-b^{2} / a^{2}}\). Si\(a\) =\(b\), o \(e\) = 0, la elipse se convierte en un círculo.
La característica más llamativa de las órbitas elípticas bajo la influencia de la fuerza\(1/r^2\) gravitacional es que el “objeto central” (el sol, por ejemplo, si nos interesa la órbita de un planeta, asteroide o cometa) no está en el centro geométrico de la elipse. Más bien, se encuentra en un punto especial llamado foco de la elipse (etiquetada con “O” en la figura, ya que ese es el origen para el vector de posición del cuerpo en órbita). En realidad hay dos focos, colocados simétricamente en el eje horizontal (mayor), y la distancia de cada foco al centro de la elipse viene dada por el producto\(ea\), es decir, el producto de la excentricidad y el eje semimajor. (Esto explica por qué la “excentricidad” se llama así: es una medida de lo “descentrado” que está el foco.)
Para un objeto que se mueve en una órbita elíptica alrededor del sol, la distancia al sol es mínima en un punto llamado perihelio, y máxima en un punto llamado afelio. Esos puntos se muestran en la figura y se etiquetan como “P” y “A”, respectivamente. Para un objeto en órbita alrededor de la tierra, los términos correspondientes son perigeo y apogeo; para una órbita alrededor de algún cuerpo central no especificado, se utilizan los términos periapsis y apoapsis. Existe cierta confusión en cuanto a si las distancias deben medirse desde la superficie o desde el centro del cuerpo central; aquí asumiré que todas se miden desde el centro, en cuyo caso las siguientes relaciones siguen directamente de la Figura \(\PageIndex{3}\):
La elipse que he dibujado en la Figura \(\PageIndex{3}\) es en realidad demasiado excéntrica para representar la órbita de cualquier planeta en el sistema solar (aunque bien podría ser la órbita de un cometa). El planeta con la órbita más excéntrica es Mercurio, y eso es sólo\(e\) = 0.21. Esto significa que \(b\) = 0.978\(a\), una desviación casi imperceptible de un círculo. He dibujado la órbita a escala en Figura\(\PageIndex{4}\), y como se puede ver la única manera que se puede decir que es una elipse es, precisamente, porque el sol no está en el centro.
Figura\(\PageIndex{4}\): Órbita de Mercurio, con la suma aproximada a escala
Dado que una elipse solo tiene dos parámetros, y tenemos dos constantes del movimiento (la energía total\(E\),, y el momento angular,\(L\)), deberíamos poder determinar cómo será la órbita basándose solo en esas dos cantidades. Bajo el supuesto que estamos haciendo aquí, que el objeto muy masivo no se mueve en absoluto, la energía total del sistema es justa
\ [E=\ frac {1} {2} m v^ {2} -\ frac {G M m} {r}\ etiqueta {eq:10.13}.\]
Para una órbita circular, el radio\(R\) determina la velocidad (según la Ecuación (\ ref {eq:10.11}), y de ahí la energía total, que se ve fácilmente que es\(E=-\frac{G M m}{2 R}\). Resulta que esta fórmula es válida también para órbitas elípticas, si se sustituye el eje semimajor\(a\) por\(R\):
\ [E=-\ frac {G M m} {2 a}\ etiqueta {eq:10.14} .\]
Tenga en cuenta que la energía total (\ ref {eq:10.14}) es negativa. Esto significa que tenemos una órbita encuadernada, con lo que quiero decir, una situación en la que el objeto orbitante no tiene suficiente energía cinética para volar arbitrariamente lejos del centro de atracción. En efecto, ya que \(U^G \rightarrow 0\) como\(r \rightarrow \infty\), se puede ver en la Ecuación (\ ref {eq:10.13}) que si los dos objetos pudieran estar infinitamente lejos, la energía total eventualmente tendría que ser positiva, para cualquier velocidad distinta de cero del objeto más ligero. Entonces, si \(E < 0\), tenemos órbitas encuadernadas, que son elipses (de las cuales un círculo es un caso especial), y a la inversa, si\(E > 0\) tenemos trayectorias “desunidas”, que resultan ser hipérbolas 4. Estas trayectorias simplemente pasan cerca del centro de atracción una vez, y nunca regresan.
El caso límite especial cuando\(E\) = 0 corresponde a una trayectoria parabólica. En este caso, la partícula tampoco regresa nunca: tiene apenas la energía cinética suficiente para hacerla “hasta el infinito”, ralentizando todo el tiempo, así \(v \rightarrow 0\) como\(r \rightarrow \infty\). La velocidad inicial necesaria para lograr esto, comenzando desde una distancia inicial\(r_i\), se suele llamar la “velocidad de escape” (aunque realmente debería llamarse la velocidad de escape), y se encuentra simplemente estableciendo la Ecuación (\ ref {eq:10.13}) igual a cero, con \(r = r_i\), y resolviendo para\(v\):
\ [v_ {e s c} =\ sqrt {\ frac {2 G M} {r_ {i}}} \ etiqueta {eq:10.15}.\]
En general, se puede calcular la velocidad de escape desde cualquier distancia inicial\(r_i\) hasta el objeto central, pero la mayoría de las veces se calcula a partir de su superficie. Tenga en cuenta que \(v_{esc}\) no depende de la masa del objeto más ligero (siempre asumiendo que el objeto más pesado no se mueve en absoluto). La velocidad de escape de la superficie de la tierra es de unos 11 km/s, o 1.1×10 4 m/s; pero esto por sí solo no sería suficiente para dejar atrás la atracción del sol. La velocidad de escape del sol a partir de un punto de la órbita terrestre es de 42 km/s.
Para resumir todo lo anterior, suponga que está tratando de poner algo en órbita alrededor de un cuerpo mucho más masivo, y empiezas a una\(r\) distancia del centro de ese cuerpo. Si le das al objeto una velocidad menor que la velocidad de escape en ese punto, el resultado será\(E\) < 0 y una órbita elíptica (de la cual un círculo es un caso especial, si le das la velocidad precisa\(v=\sqrt{G M / r}\) en la dirección correcta). Si le das precisamente la velocidad de escape (\ ref {eq:10.15}), la energía total del sistema será cero y la trayectoria del objeto será una parábola; y si le das más velocidad que\(v_{esc}\), la energía total será positiva y la trayectoria será una hipérbola. Esto se ilustra en la Figura \(\PageIndex{5}\) a continuación.
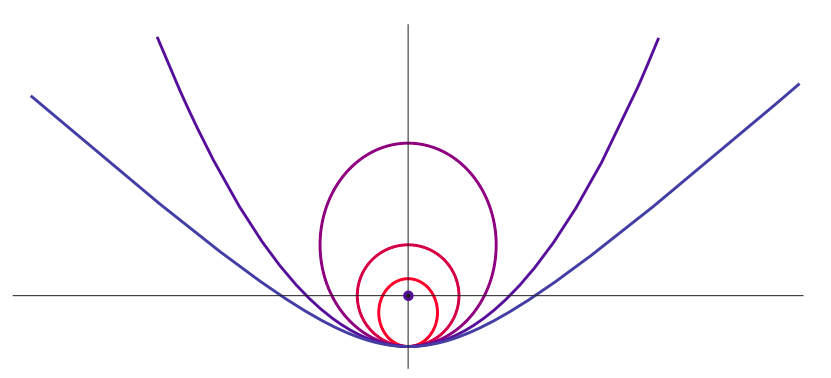
Figura\(\PageIndex{5}\): Posibles trayectorias para un objeto que se “libera” con una velocidad lateral en el punto más bajo de la figura, bajo la atracción gravitacional de una gran masa representada por el círculo negro. Cada trayectoria corresponde a un valor diferente de la energía cinética inicial del objeto: si\(K_{circ}\) es la energía cinética necesaria para tener una órbita circular a través del punto de liberación, la figura muestra los casos\(K_i = 0.5K_{circ}\) (elipse pequeña),\ (K_i = K_ {circ}\) (círculo),\(K_i = 1.5K_{circ}\) (grande elipse),\ (k_i = 2K_ {circ}\) (velocidad de escape, parábola) y\(K_i = 2.5K_{circ}\) (hipérbola).
Obsérvese que todas las trayectorias mostradas en la Figura\(\PageIndex{5}\) tienen la misma energía potencial en el “punto de liberación” (ya que la distancia desde ese punto hasta el centro de atracción es la misma para todos), por lo que aumentar la energía cinética en ese punto también significa aumentar la energía total (\ ref { eq:10.13}) (que es constante en todo momento). Por lo que la imagen muestra diferentes órbitas en orden de aumentar la energía total.
Para una energía total dada, el momento angular total no cambia la naturaleza fundamental de la órbita (unida o no unida), sino que puede marcar una gran diferencia en la forma de la órbita. En términos generales, para una energía dada las órbitas con menor momento angular serán “más estrechas” o “más reducidas” que las que tienen más momento angular, ya que un momento angular inicial más pequeño en el punto de inserción significa una componente de velocidad lateral más pequeña. En el caso extremo del momento angular inicial cero (sin velocidad lateral en absoluto), la trayectoria, independientemente de la energía total, se reduce a una línea recta, ya sea recta hacia o directamente desde el centro de atracción.
Para órbitas elípticas, se puede probar el resultado
\ [e=\ sqrt {1-\ frac {L^ {2}} {a G M m^ {2}}}\ label {eq:10.16}\]
que muestra cómo la excentricidad aumenta a medida que\(L\) disminuye, para un valor dado de\(a\) (es decir, para una energía total dada). Debería al menos bosquejar cómo obtener este resultado, ya que es una variante de un procedimiento que quizás tengas que usar para algunos problemas de tareas este semestre. Se inicia escribiendo el momento angular como\(L = mr_Pv_P\) (o \(mr_Av_A\)), donde\(A\) y\(P\) son los puntos especiales que se muestran en la Figura\(\PageIndex{3}\), donde\(\vec v\) y\(\vec r\) son perpendiculares. Entonces, se nota que\(r_P = r_{min} = (1 − e)a\) (o, alternativamente,\(r_A = r_{max} = (1 + e)a\)), así que\ (v_p = L/ [m (1− e) a]\). Luego sustituya estas expresiones por\(r_P\) y \(v_P\) en Ecuación (\ ref {eq:10.13}), establezca el resultado igual a la energía total (\ ref {eq:10.14}), y resuelva para\(e\).
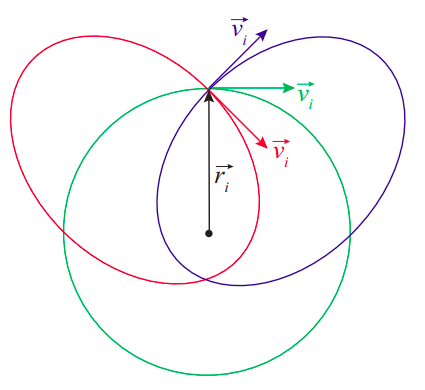
Figura\(\PageIndex{6}\): Efecto del “ángulo de inserción” sobre la órbita.
La figura \(\PageIndex{6}\) ilustra el efecto de variar el momento angular, para una energía dada. Todos los vectores de velocidad iniciales en la figura tienen la misma magnitud, y el punto de liberación (con vector de posición\(\vec r_i\)) es el mismo para todas las órbitas, por lo que todos tienen la misma energía; de hecho, se puede comprobar que el eje semimajor de las dos elipses es el mismo que el radio de la circle, como lo requiere la Ecuación (\ ref {eq:10.14}). La diferencia entre las órbitas es su momento angular total. La órbita verde tiene el momento angular máximo posible a la energía dada, ya que el vector de velocidad verde es perpendicular a\ (\ vec r_i\). Tenga en cuenta que esto (maximizando\(L\) para un\(E\) < 0 dado) siempre resulta en un círculo, de acuerdo con la Ecuación (\ ref {eq:10.15}): la excentricidad es cero cuando\ (L=L_ {c i r c}\ equiv\ sqrt {a G M m^ {2}}\), que es el mayor valor\(L\) permitido en la Ecuación (\ ref {eq:10.15}) .
Para las otras dos órbitas,\(\vec v_i\) y\(\vec r_i\) hacer ángulos de 45\(^{\circ}\) y 135\(^{\circ}\), y así el momento angular\(L\) tiene magnitud \(L=L_{\text {circ}} \sin 45^{\circ}=L_{\text {circ}} / \sqrt{2}\). El resultado son las elipses roja y azul, con excentricidades \(e=\sqrt{1-\sin ^{2}\left(45^{\circ}\right)}\) = 0.707.
4 Al parecer hay una manera de describir una hipérbola como una elipse con excentricidad\(e\) > 1, pero definitivamente no voy a ir ahí.
Leyes de Kepler
El primer gran éxito de la teoría de Newton fue dar cuenta de los resultados que Johannes Kepler había extraído de datos astronómicos sobre el movimiento de los planetas alrededor del sol. Kepler había logrado encontrar una serie de regularidades en una montaña de datos (la mayoría de los cuales eran observaciones de su mentor, el astrónomo danés Tycho Brahe), y las expresó de manera sucinta en forma matemática. Estos resultados han llegado a conocerse como leyes de Kepler, y son los siguientes:
- Los planetas se mueven alrededor del sol en órbitas elípticas, con el sol en un foco de la elipse
- (Ley de áreas) Una línea que conecta el planeta con el sol (el vector de posición del planeta) barre áreas iguales en tiempos iguales.
- El cuadrado del periodo orbital de cualquier planeta es proporcional al cubo del eje semimajor de su órbita (la misma constante de proporcionalidad se mantiene para todos los planetas).
He discutido extensamente la primera “ley” en la sección anterior, y también señalé que la matemática necesaria para probarla está lejos de ser trivial. La segunda ley, en cambio, si bien suena complicada, resulta ser una consecuencia directa de la conservación del momento angular. Para ver lo que significa, considere Figura \(\PageIndex{7}\).
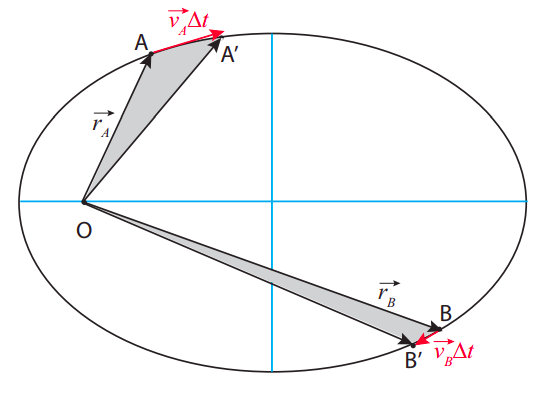
Figura \(\PageIndex{7}\): Ilustrando la ley de áreas de Kepler. Los dos “triángulos curvos” grises tienen la misma área, por lo que la partícula debe tomar el mismo tiempo para pasar de A a A que\(^{\prime}\) lo hace para pasar de B a\(^{\prime}\) B.
Supongamos que, en algún momento\(t_A\), la partícula está en el punto A, y un tiempo\(\Delta t\) después se ha trasladado a\(^{\prime}\) A. El área “barrida” por su vector de posición se muestra en gris en la figura, y la segunda ley de Kepler establece que debe ser la misma, para el mismo intervalo de tiempo, en cualquier punto de la trayectoria; así, por ejemplo, si la partícula comienza en B en su lugar, entonces en el mismo intervalo de tiempo\(\Delta t\) lo hará moverse a un punto B\(^{\prime}\) tal que el área del “ triángulo curvo” OBB\(^{\prime}\) sea igual al área de OAA\(^{\prime}\).
Cualitativamente, esto significa que la partícula necesita moverse más lentamente cuando está más lejos del centro de atracción, y más rápido cuando está más cerca. Cuantitativamente, ¡ esto en realidad solo significa que su momento angular es constante! Para ver esto, tenga en cuenta que la distancia recta de A a A\(^{\prime}\) es el vector de desplazamiento\ ( \ Delta\ vec {r} _A\), que, para un intervalo suficientemente corto\(\Delta t\), será aproximadamente igual a\(\vec{v}_A \Delta t\). Nuevamente, para pequeños\(\Delta t\), el área del triángulo curvo será aproximadamente la misma que la del triángulo recto OAA\(^{\prime}\). Es un resultado bien conocido en trigonometría que el área de un triángulo es igual a 1/2 el producto de las longitudes de cualquiera de sus dos lados por el seno del ángulo que forman. Entonces, si los dos triángulos en las figuras tienen las mismas áreas, debemos tener
\ [\ izquierda|\ vec {r} _ {A}\ derecha|\ izquierda|\ vec {v} _ {A}\ derecha|\ Delta t \ sin\ theta_ {A} =\ izquierda|\ vec {r} _ {B} _ {B}\ derecha|\ derecha|\ vec {v} _ {B}\ derecha| Delta\ t\ sin\ theta_ {B}\ etiqueta {eq:10.17}\]
y reconocemos aquí la condición \(\left|\vec{L}_{\boldsymbol{A}}\right|=\left|\vec{L}_{B}\right|\) , es decir, conservación del momento angular. (Una vez establecido el resultado para infinitesimalmente pequeños\(\Delta t\), podemos establecerlo para áreas de tamaño finito usando cálculo integral, es decir, en esencia, dividiendo triángulos grandes en sumas de muchos pequeños).
En cuanto al tercer resultado de Kepler, es fácil de establecer para una órbita circular, y definitivamente no es fácil para una elíptica. Llamemos\(T\) al período orbital, es decir, el tiempo que tarda en que el objeto menos masivo rodee la órbita una vez. Para una órbita circular, la velocidad angular \(\omega\) puede escribirse en términos de\(T\) as\ (\ omega = 2\ pi/T\), y de ahí la velocidad regular\ (v = R\ omega = 2\ pi R/T\). Sustituyendo esto en la Ecuación (\ ref {eq:10.11}), obtenemos\ (GM/R^2 = 4\ pi^ {2} R/T^ {2}\), que se puede simplificar aún más para leer
\ [T^ {2} =\ frac {4\ pi^ {2}} {G M} R^ {3} \ label {eq:10.18}.\]
Nuevamente, esto resulta funcionar para una órbita elíptica si reemplazamos\(R\) por\(a\).
Obsérvese que la constante de proporcionalidad en la Ecuación (\ ref {eq:10.18}) depende únicamente de la masa del cuerpo central. Para el sistema solar, ese sería el sol, por supuesto, y entonces la fórmula se aplicaría a cualquier planeta, asteroide, o cometa, con la misma constante de proporcionalidad. Esto te da una manera rápida de calcular el periodo orbital de cualquier cosa que orbita el sol, si conoces su distancia (o viceversa), con base en el hecho de que sabes cuáles son estas cantidades para la Tierra.
De manera más general, supongamos que tienes dos planetas, 1 y 2, ambos orbitando la misma estrella, a distancias\(R_1\) y\(R_2\), respectivamente. Entonces sus periodos orbitales\(T_1\) y \(T_2\) deben satisfacer\ (T_ {1} ^ {2} =\ left (4\ pi^ {2}/G M\ right) R_ {1} ^ {3}\) y\ (T_ {2} ^ {2} =\ left (4\ pi^ {2}/G M\ right) R_ {2} ^ {3}\). Divide una ecuación entre la otra, y la constante de proporcionalidad se cancela, así obtienes
\ [\ izquierda (\ frac {T_ {2}} {T_ {1}}\ derecha) ^ {2} =\ izquierda (\ frac {R_ {2}} {R_ {1}}\ derecha) ^ {3} \ label {eq:10.19}.\]
A partir de esto, alguna manipulación simple te da
\ [T_ {2} =T_ {1}\ izquierda (\ frac {R_ {2}} {R_ {1}}\ derecha) ^ {3/2} \ label {eq:10.20}.\]
Tenga en cuenta que puede expresar\(R_1\) y \(R_2\) en cualquier unidad que desee, siempre y cuando utilice las mismas unidades para ambos, y de manera similar\(T_1\) y\(T_2\). Por ejemplo, si usas a la Tierra como tu referencia “planeta 1", entonces sabes que \(T_1\) = 1 (en años), y\(R_1\) = 1, en AU (una UA, o “unidad astronómica”, es la distancia de la Tierra al sol). Un planeta hipotético a una distancia de 4 UA del sol debería tener entonces un período orbital de 8 años terrestres, ya que\ (4^ {3/ 2} =\ sqrt {4^ {3}} =\ sqrt {64} =8\).
Una fórmula igual a (\ ref {eq:10.18}), pero con una constante de proporcionalidad diferente, se aplicaría a los satélites de cualquier planeta dado; por ejemplo, la miríada de satélites artificiales que orbitan la Tierra. De nuevo, se podría introducir un “satélite de referencia” etiquetado como 1, con periodo y distancia conocidos a la Tierra (¿la luna, por ejemplo?) , y derivar nuevamente el resultado (\ ref {eq:10.20}), que te permitiría obtener el periodo de cualquier otro satélite, si supieras cómo se compara su distancia a la tierra con la de la luna (o, a la inversa, la distancia a la que necesitarías colocarla para obtener un periodo orbital deseado).
Por ejemplo, supongamos que quiero colocar un satélite en una órbita “geosincrónica”, es decir, que tarda 1 día en orbitar la Tierra. Sé que la luna tarda 29 días, así que puedo escribir la Ecuación (\ ref {eq:10.20}) como\(1 = 29(R_2/R_1)^{3/2}\), o, resolviéndola,\(R_2/R_1 = (1/29)^{2/3} = 0.106\), es decir, el satélite tendría que estar aproximadamente 1/10 de la distancia Tierra-Luna de (el centro de) la Tierra.
En retrospectiva, es algo notable que las leyes de Kepler sean tan precisas, para el sistema solar, como resultaron ser, ya que solo pueden derivarse matemáticamente de la teoría de Newton haciendo una serie de aproximaciones simplificadoras: que el sol no se mueve, que el gravitacional fuerza de los otros planetas no tiene efecto en la órbita de cada planeta, y que los planetas (y el sol) son esferas perfectas, por ejemplo. Las dos primeras de estas aproximaciones funcionan tan bien como lo hacen porque el sol es tan masivo; la tercera funciona porque los tamaños de todos los objetos involucrados (incluido el sol) son mucho más pequeños que las órbitas correspondientes. Sin embargo, el trabajo de Newton dejó claro que las leyes de Kepler solo podían ser aproximadamente válidas, y los científicos pronto se pusieron a trabajar en desarrollar formas de calcular las correcciones necesarias para tratar, por ejemplo, las trayectorias de los cometas o la órbita de la luna.
De las principales aproximaciones que he enumerado anteriormente, la más fácil de deshacerme (matemáticamente) es la primera, es decir, que el sol no se mueve. En cambio, lo que uno encuentra es que, mientras el sol y el planeta sigan siendo tratados como un sistema aislado, ambos girarán alrededor del centro de masa del sistema. Por supuesto, el movimiento del sol (un ligero “bamboleo”) es muy pequeño, pero no del todo despreciable. Incluso se puede ver en la simulación que mencioné anteriormente, en
phet.colorado.edu/es/simulación/gravedad-y-órbitas.
Lo que es mucho más difícil de tratar, matemáticamente, es el hecho de que ninguno de los planetas del sistema solar en realidad forma un sistema aislado con el sol, ya que todos los planetas están realmente tirando gravitacionalmente el uno del otro todo el tiempo. Particularmente, Júpiter y Saturno tienen una influencia no despreciable en las órbitas del otro, y en las órbitas de todos los demás planetas, que sólo pueden percibirse a lo largo de los siglos. Básicamente, las órbitas siguen pareciendo elipses en muy buen grado, pero las elipses giran muy, muy lentamente (por lo que no logran cerrarse exactamente sobre sí mismas). Este efecto, conocido como precesión orbital, es más dramático para Mercurio, donde los ejes de la elipse giran más de un grado por siglo.
Sin embargo, la teoría newtoniana es tan precisa, y las técnicas de cálculo desarrolladas a lo largo de los siglos tan sofisticadas, que a principios del siglo XX la precesión de las órbitas de todos los planetas excepto Mercurio había sido calculada casi exactamente de acuerdo con los mejores datos observacionales. La discrepancia inexplicable para Mercurio ascendió sólo a 43 segundos de arco por siglo, de 5600 (un error de sólo 0.8%). Finalmente fue resuelto por la teoría general de la relatividad de Einstein.