2.2: Planitud

Objetivos de aprendizaje

• Estudiar el concepto de transporte paralelo
• Planitud del espacio-tiempo

Fracaso del paralelismo

En Postulado P1 asumimos implícitamente que dados dos puntos, había un cierto vector que los conectaba. Esto es análogo al postulado euclidiano de que dos puntos definen una línea. Para obtener una idea, pensemos en cómo podría fallar la versión euclidiana de esta suposición. La geometría euclidiana es solo una descripción aproximada de la superficie terrestre, por ejemplo, y es por ello que los mapas planos siempre conllevan distorsiones de las formas reales. Las distorsiones podrían ser despreciables en un mapa de Connecticut, pero severas para un mapa del mundo entero. Es decir, el globo es sólo localmente euclidiana. Sobre una superficie esférica, el objeto apropiado para desempeñar el papel de una “línea” es un gran círculo, Figura\(\PageIndex{1}\). Las líneas de longitud son ejemplos de grandes círculos, y como todos estos coinciden en los polos, podemos ver que dos puntos no determinan una línea en geometría noneúclida.

Figura\(\PageIndex{1}\): Un avión que vuela de la Ciudad de México a Londres sigue el camino más corto, que es un segmento de un gran círculo. Un camino de longitud extrema entre dos puntos se denomina geodésico.

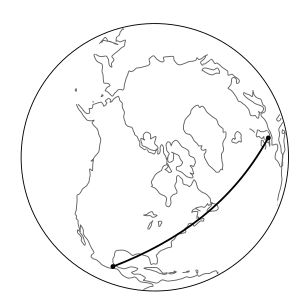
Un error bidimensional que vive en la superficie de una esfera no podría decir que la esfera estaba incrustada en una tercera dimensión, pero aún así podría detectar la curvatura de la superficie. Se podía decir que los postulados de Euclides eran falsos en escalas de gran distancia. En la figura se muestra un método que tiene un mejor análogo en el espacio-tiempo\(\PageIndex{2}\): transportar un vector de un punto a otro depende de la trayectoria por la que se transportó. Este efecto es nuestra definición de curvatura.

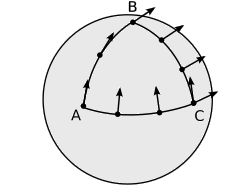
Figura\(\PageIndex{2}\) : Transportar el vector a lo largo de la ruta\(\overrightarrow{AC}\) da un resultado diferente al de hacerlo a lo largo de la ruta ABC.

Transporte Paralelo

El tipo particular de transporte que tenemos en mente aquí se llama transporte paralelo. Cuando camino de la sala a la cocina mientras llevo un giroscopio mecánico, estoy en paralelo transportando el vector espacial indicado por la dirección de su eje. La figura\(\PageIndex{3}\) muestra que el transporte paralelo también se puede definir para vectores similares al tiempo, y que el transporte paralelo se puede definir en espacio-tiempo usando solo movimiento inercial, relojes e intersección de líneas mundiales. Los observadores a bordo de las dos naves espaciales utilizan relojes para verificar el paralelismo de sus líneas mundiales (vectores\(\overrightarrow{AB}\) y\(\overrightarrow{CD}\), que tienen la misma longitud medida por el tiempo adecuado transcurrido a bordo de las naves). Observer\(\overrightarrow{AB}\) dispara relojes a observador\(\overrightarrow{CD}\), y los relojes se configuran de manera que cuando pasan uno junto al otro, automáticamente registren las lecturas del otro. Los vectores son paralelos si el registro posteriormente revela\(\overrightarrow{AD}\) e\(\overrightarrow{BC}\) intersectó en sus puntos medios, medidos por los tiempos apropiados registrados en los relojes.

Figura\(\PageIndex{3}\): Transporte Paralelo.

La relatividad especial requiere espacio-tiempo plano

Escondida en una serie de manchas en el Capítulo 1 fue la siguiente suposición.

Postulado 2 (P2): Planitud del espacio-tiempo

El transporte paralelo de un vector de un punto a otro da un resultado que es independiente del camino por el que fue transportado.

La propiedad P2 es solo aproximadamente cierta, como lo muestra explícitamente el satélite Gravity Probe B, lanzado en 2004. La sonda portaba cuatro giroscopios hechos de cuarzo., que fueron las esferas más perfectas jamás fabricadas, variando desde la esfericidad en no más de aproximadamente\(40\) átomos. Después de un año y alrededor de\(5000\) órbitas alrededor de la tierra, se encontró que los giroscopios habían cambiado sus orientaciones en relación con las estrellas distantes en aproximadamente\(3 \times 10^{-6}\) radianes (figura\(\PageIndex{4}\)). Esta es una violación de P2, pero una que era muy pequeña y difícil de detectar. El resultado estuvo en buena concordancia con las predicciones de la relatividad general, que describe la gravedad como una curvatura del espacio-tiempo. La pequeñez del efecto nos dice que el campo gravitacional de la tierra no es tan grande como para invalidar completamente la relatividad especial como una descripción de la región cercana del espacio-tiempo.

Uno de los supuestos básicos de la relatividad general es que en una región suficientemente pequeña del espacio-tiempo, siempre es una buena aproximación asumir P2, de manera que la relatividad general es localmente la misma que la relatividad especial. En el experimento Gravity Probe B, el efecto fue pequeño y difícil de detectar, y esta fue la razón para dejar que el efecto se acumulara sobre una gran cantidad de órbitas, abarcando una gran región del espacio-tiempo. El problema Q5 en la sección de ejercicios investiga más cuantitativamente cómo varía el tamaño de los efectos de curvatura con el tamaño de la región.

Figura\(\PageIndex{4}\): Ángulo de precesión en función del tiempo medido por los cuatro giroscopios a bordo de Gravity Probe B.