Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

10.1: La relatividad requiere magnetismo

Última actualización

30 oct 2022
Guardar como PDF
- 10: Electromagnetismo
- 10.2: Campos en la Relatividad

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Explicar las siguientes leyes dentro de la Ley de Gas Ideal

La relatividad requiere magnetismo

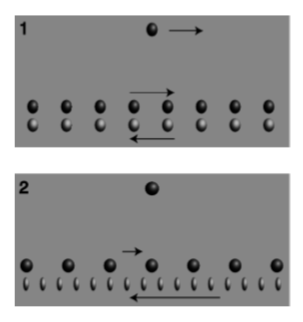
higo 10.1.1.png — Figura $\PageIndex{1}$ : Un modelo de una partícula cargada y un alambre portador de corriente, visto en dos marcos de referencia diferentes. La contracción relativista de longitud es muy exagerada. La fuerza sobre la partícula solitaria es puramente magnética en 1, y puramente eléctrica en 2.

La figura $\PageIndex{1}$ es un modelo poco realista de partículas cargadas que se mueven paralelas a un cable portador de corriente. ¿Qué fuerza eléctrica siente la partícula solitaria en la figura $\PageIndex{1}$ (1)? Dado que la densidad del “tráfico” en los dos lados de la “carretera” es igual, hay cero fuerza eléctrica general sobre la partícula solitaria. Cada “auto” que atrae a la partícula solitaria se empareja con un compañero al otro lado de la carretera que la repele. Si no supiéramos del magnetismo, pensaríamos que esta era toda la historia: la partícula solitaria no siente ninguna fuerza del cable.

La figura $\PageIndex{1}$ (2) muestra lo que veríamos si estuviéramos observando todo esto desde un marco de referencia moviéndose junto con la carga solitaria. La relatividad nos dice que los objetos en movimiento aparecen contraídos a un observador que no se mueve junto con ellos. Ambas líneas de carga están en movimiento en ambos fotogramas de referencia, pero en cuadro se $1$ movían a velocidades iguales, por lo que sus contracciones fueron iguales. En marco $2$ , sin embargo, sus velocidades son desiguales. Las cargas oscuras se mueven más lentamente que en frame $1$ , por lo que en frame $2$ están menos contraídas. Las cargas de color claro se mueven más rápidamente, por lo que su contracción es mayor ahora. Los “autos” de los dos lados de la “carretera” ya no están emparejados, por lo que las fuerzas eléctricas sobre la partícula solitaria ya no se cancelan como lo hicieron en $\PageIndex{1}$ (1). La partícula solitaria es atraída por el alambre, porque las partículas que lo atraen son más densas que las que lo repelen.

Ahora observadores en marcos $1$ y $2$ no están de acuerdo sobre muchas cosas, pero sí están de acuerdo en hechos concretos. El observador $2$ va a ver la partícula solitaria derivar hacia el cable debido a la atracción eléctrica del cable, acelerando gradualmente y eventualmente golpeando el cable. Si $2$ ve esta colisión, entonces $1$ debe también. Pero $1$ sabe que la fuerza eléctrica total sobre la partícula solitaria es exactamente cero. Debe haber algún nuevo tipo de fuerza. Ella inventa un nombre para ello: el magnetismo.

El magnetismo es un efecto puramente relativista. Dado que los efectos relativistas se han reducido en un factor de $v^2$ comparación con los newtonianos, es sorprendente que la relatividad pueda producir un efecto tan vigoroso como la atracción entre un imán y tu refrigerador. La explicación es que aunque la materia es eléctricamente neutra, la cancelación de fuerzas eléctricas entre objetos macroscópicos es extremadamente delicada, por lo que cualquier cosa que arroje la cancelación, aunque sea ligeramente, conduce a una fuerza sorprendentemente grande.

La relatividad requiere magnetismo

Support Center

How can we help?