10.4: Transformación de los Campos

Objetivos de aprendizaje

• Explicar las siguientes leyes dentro de la Ley de Gas Ideal

Dado que hemos asociado los componentes de los campos eléctrico y magnético con elementos de un tensor de rango 2, la ley de transformación para estos campos se deriva ahora de la ley general de transformación de tensores para\(2\) tensores de rango (sección 9.2). Primero declaramos la regla general, en una forma prettificada, y luego damos algunos ejemplos concretos. Bajo un impulso por una velocidad de tres\(\vec{v}\), los campos eléctricos y magnéticos\(\vec{E}\) y se\(\vec{B}\) transforman a\(\vec{E}'\) y de\(\vec{B}'\) acuerdo con estas reglas:

Ejemplo\(\PageIndex{1}\): A line of charge

Figura\(\PageIndex{1}\): Una línea de carga.

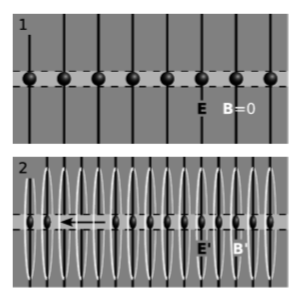
La figura\(\PageIndex{1}\) (1) muestra una línea de cargas. En un punto cercano dado, crea un campo eléctrico\(E\) que apunta hacia afuera, medido por un observador\(o\) que está en reposo relativo a las cargas. Este campo está representado en la figura por su patrón de líneas de campo, que comienzan en las cargas e irradian hacia afuera como las cerdas de un cepillo de botella. Debido a que las cargas están en reposo, el campo magnético es cero. (Encontrar la magnitud del campo a cierta distancia es una aplicación sencilla de la ley de Gauss.)

Consideremos ahora un observador\(o'\), figura\(\PageIndex{1}\) (2), moviéndose a velocidad\(v\) hacia la derecha con relación a\(o\). Sin siquiera preocuparnos por cómo se creó el campo, podemos transformar los campos, en el punto en el espacio discutido anteriormente, en el nuevo marco. El resultado es\(E' = γE\) y\(B'_⊥ = -γv × E\). En este marco, el campo eléctrico es más intenso, y también hay un campo magnético, cuyo patrón de líneas de campo blanco forma círculos que se encuentran en planos perpendiculares a la línea. Si por casualidad sabemos que el campo fue creado por la línea de carga, que se mueve según\(o'\), entonces podemos explicar estos resultados como derivados de dos efectos. En primer lugar, la línea de carga ha sido contratada por longitud. Esto hace que la densidad de carga por unidad de longitud aumente en un factor de\(γ\), con un incremento proporcional en el campo eléctrico. En la descripción de la línea de campo, simplemente tenemos más cargos en la figura, por lo que hay más líneas de campo que salen de ellas. Segundo, la línea de carga se mueve hacia la izquierda en este cuadro, por lo que forma una corriente eléctrica, y esta corriente es la causa del campo magnético\(B'\).

Ejemplo\(\PageIndex{2}\): A moving charge

Figura\(\PageIndex{2}\): Una carga en movimiento.

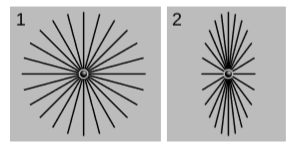
La figura\(\PageIndex{2}\) (1) muestra las líneas de campo eléctrico de una carga, en el marco de reposo de la carga\(K\). En la figura\(\PageIndex{2}\) (2) vemos el mismo campo eléctrico, en un marco\(K'\) en el que la carga se mueve a lo largo del\(x\) eje -eje, que apunta a la derecha, a\(90\%\) de\(c\). (En este cuadro también hay un campo magnético, el cual no se muestra.) Este campo eléctrico, que varía en el tiempo, se muestra como una instantánea en un hiperplano de simultaneidad\(t' = 0\) de\(K'\). Sorprendentemente, todas estas líneas de campo apuntan hacia la posición actual de la carga en\(K'\).

Las perturbaciones en el campo electromagnético se propagan a\(c\), no instantáneamente, por lo que uno podría haber esperado que el campo\(P\) en una determinada ubicación de esta figura apuntara hacia una ubicación a una distancia\(r\) que la carga había ocupado en un momento anterior\(t' = -r/c\). Esto habría producido un conjunto de líneas curvas de campo que recuerdan a la estela de un barco. Para ver que esto no es posible, considere el punto\((0, 0, h, 0)\) en las coordenadas Minkowski de\(K\), es decir, un punto en el\(y\) eje -eje. Después de una transformación de Lorentz a lo largo\(x\), las coordenadas de este punto en\(K'\) siguen siendo\((0, 0, h, 0)\), por lo que también se encuentra en una línea que pasa transversalmente a través de la posición actual de la carga.\(K'\) Dado que este punto tiene\(E_x = 0\) y\(\vec{B} = 0\) en\(K\), la aplicación de las leyes de transformación demuestra eso\(E'_x = 0\) también, de manera que el campo apunta hacia la posición actual de la carga, no su posición pasada.

Un cálculo similar pero más complicado muestra que el campo en ángulos intermedios también se encuentra en la dirección instantánea radial. En lugar de rellenar los detalles, observamos que esto tiene sentido porque el vector Poynting\(\vec{E} × \vec{B}\) entonces no tiene componente radial, que es como se esperaba porque la energía debe transportarse hacia adelante pero no irradiarse hacia afuera.

A uno le podría preocupar que esto indicara que la información sobre la posición del cargo se propagaba instantáneamente, contradiciendo la relatividad. Pero este es un cargo que siempre ha estado en su actual estado de movimiento y siempre lo estará. Si el movimiento de la carga hubiera sido perturbado por alguna fuerza externa en un momento posterior al\(t' = -r/c\), las líneas de campo en\(K\) seguirían apuntando hacia la ubicación que la carga había ocupado anteriormente mientras estaba en reposo, y el campo en\(K'\) estaría apuntando hacia su linealmente extrapolado posición.

Ejemplo\(\PageIndex{3}\): A field behaving like a stick

La figura\(\PageIndex{2}\) (2) aparece idéntica a una copia de la figura\(\PageIndex{2}\) (1) que ha sido contratada por Lorentz\(1/γ\), y podemos verificar a partir de las leyes de transformación para los campos que esto es correcto. Dado que estas leyes de transformación se aplican independientemente de cómo se produjeron los campos, tenemos una regla general, que es que si un campo es puramente eléctrico en un cuadro, entonces su dirección se transforma en otro marco de la misma manera que la dirección de un palo, cuando transformamos fuera del marco de reposo del palo.

No es cierto en general que las líneas de campo eléctrico simplemente puedan ser transportadas de un marco a otro como si fuéramos Lorentz contratando un nido de ratas construido con alambre. Esta propiedad se sostiene solo cuando el marco original es de un tipo muy especial: un marco en el que el campo es puramente eléctrico. (Siempre podemos encontrar tal marco si\(E^2 > B^2\); ver sección 10.5.) Como contraejemplo a la noción de que se aplica de manera más general, consideremos el caso en el que un campo es puramente magnético en un determinado marco. Entonces las líneas de campo eléctrico ni siquiera existen en el marco original, sino que sí existen en el nuevo.

Volviendo al caso en el que el campo original es puramente eléctrico, para que el comportamiento de palo sí se mantenga, no es inmediatamente obvio por qué debería haber esta extraña correspondencia entre palos y líneas de campo. Los métodos utilizados en el problema Q3 del capítulo 2 no parecen tener mucho en común con los que hemos utilizado para determinar cómo se comporta el campo eléctrico. Pero el siguiente argumento físico muestra que hay una razón simple para el comportamiento idéntico.

Considera un palo con cargas\(+q\) y\(-q\) fijado en los extremos. El palo no gira y se mueve inercialmente. En el marco de reposo del palo\(K\), hay una línea de campo que se origina\(+q\) y termina en la\(-q\) que coincide con el palo. Ahora considere el marco\(K'\) moviéndose en alguna dirección relativa al palo. Como se discutió en el ejemplo 10.4.2, el campo debido a cada carga apunta hacia o lejos de su posición instantánea actual\(K'\) tanto en como\(K\). Por lo tanto cada campo, en el palo, es paralelo al palo, y nuevamente tenemos una línea de campo en\(K'\) que coincide con el palo. Dado que la transformación del campo es independiente de cómo se creó el campo, esto es válido para cualquier campo que sea puramente eléctrico en el marco original.