10.2: Campos en la Relatividad
- Page ID
- 126819
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Explicar por qué la ley de Coulomb no puede extenderse para incluir el magnetismo
Con base en lo que aprendimos en la sección 10.1, el siguiente paso natural parecería ser encontrar alguna manera de extender la ley de Coulomb para incluir el magnetismo. Por ejemplo, podríamos tratar de encontrar una fórmula para la fuerza magnética entre cargas\(q^1\) y\(q^2\) basada no sólo en sus posiciones relativas sino también en sus velocidades. Las siguientes consideraciones, sin embargo, nos dicen que no vayamos por ese camino.
Retrasos de tiempo en Fuerzas Ejercidas a Distancia
La relatividad prohíbe la acción instantánea de Newton a distancia. Dado que las fuerzas no pueden transmitirse instantáneamente, se vuelve natural imaginar los efectos de fuerza extendiéndose hacia afuera desde su fuente como ondas en un estanque, y entonces no tenemos más remedio que imputar alguna realidad física a estas ondas. Nosotros los llamamos campos, y ellos tienen su propia existencia independiente.
Incluso el espacio vacío, entonces, no es perfectamente carente de características. Tiene propiedades medibles. Por ejemplo, podemos dejar caer una roca para medir la dirección del campo gravitacional, o usar una brújula magnética para encontrar la dirección del campo magnético. Este concepto causó una profunda impresión en Einstein cuando era niño. Recordó que cuando tenía cinco años, el don de una brújula magnética le convenció de que había “algo detrás de las cosas, algo profundamente oculto”.
Los campos llevan energía
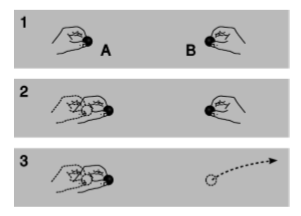
El argumento del fumador-arma para esta extraña noción de ondas de fuerza viajera proviene del hecho de que transportan energía. En la figura\(\PageIndex{1}\) (1), Alice y Betty mantienen cargas positivas\(A\) y\(B\) a cierta distancia la una de la otra. Si Alice opta por acercar su carga a Betty's, figura\(\PageIndex{1}\) (2), Alice tendrá que hacer algunos trabajos mecánicos contra la repulsión eléctrica, quemando algunas de las calorías de esa tarta de queso de chocolate que comió en el almuerzo. Esta reducción en la energía química de su cuerpo se compensa con un aumento correspondiente en la energía potencial eléctrica\(q∆V\). No sólo eso, sino que Alice siente que la resistencia se endurece a medida que las cargas se acercan y la repulsión se fortalece. Ella tiene que hacer un poco de trabajo extra, pero todo esto está debidamente contabilizado en la energía potencial eléctrica.
Pero ahora supongamos, figura\(\PageIndex{1}\) (3), que Betty decide jugarle una mala pasada a Alice lanzando carga\(B\) muy lejos justo cuando Alice se está preparando para mover carga\(A\). Ya hemos establecido que Alice no puede sentir el movimiento de la carga B instantáneamente, por lo que las fuerzas eléctricas en realidad deben ser propagadas por un campo eléctrico. Por supuesto que este experimento es totalmente poco práctico, pero supongamos por el bien del argumento que el tiempo que tarda el cambio en el campo eléctrico para propagarse a través del diagrama es lo suficientemente largo como para que Alice pueda completar su movimiento antes de que sienta el efecto de la desaparición\(B\) de. Ella todavía está recibiendo información rancia sobre\(B\) la posición de su. Al moverse\(A\) hacia la derecha, siente una repulsión, porque el campo en su región del espacio sigue siendo el campo causado por\(B\) en su antigua posición. Ella ha quemado algunas calorías de tarta de queso con chocolate, y parece que se ha violado la conservación de energía, debido a que estas calorías no pueden ser debidamente contabilizadas por ninguna interacción con\(B\), lo cual se ha ido hace mucho tiempo.
Si esperamos preservar la ley de conservación de la energía, entonces la única conclusión posible es que el propio campo eléctrico se lleva la energía del pastel de queso. De hecho, este ejemplo representa un método poco práctico de transmisión de ondas de radio. Alice sí trabaja a cargo\(A\), y esa energía entra en las ondas de radio. Aunque nunca\(B\) hubieran existido, las ondas de radio seguirían llevando energía, y Alice habría tenido que trabajar para crearlas.
Los campos deben tener leyes de transformación
En la discusión anterior he sido culpable de hacer argumentos de que los campos eran “reales”. Lo siento. En la física, y particularmente en la relatividad, suele ser una pérdida de tiempo preocuparse por si algún efecto como la contracción de la longitud es “real” o solo “parece así”. Pero pensar en los campos como tener una existencia independiente sí conduce a un principio rector útil, que es que los campos deben tener leyes de transformación. Supongamos que en un lugar determinado, el observador\(o_1\) mide todos los campos posibles: eléctrico, magnético, corpido-ripper-sexual-atraccional, y así sucesivamente. (El campo gravitacional no está en la lista, por las razones discutidas en la sección 5.2.) Observador\(o_2\), pasando por el mismo evento pero en un estado de movimiento diferente, podría realizar mediciones similares. Estamos hablando de mediciones que se llevan a cabo en una pulgada cúbica de vacío puro, pero supongamos que la respuesta a la famosa pregunta de Peggy Lee es “Sí, eso es todo lo que hay” — la única información que hay que saber sobre ese paquete vacío de la nada es el valor (dependiente del marco) de los campos que contiene. Entonces\(o_1\) debería ser capaz de predecir los resultados de las mediciones de\(o_2\)'s. Porque si no es así, ¿cuál es la naturaleza de la información a la que se le oculta\(o_1\) pero a la que se revela\(o_2\)? Presumiblemente esto sería algo relacionado con cómo los campos fueron producidos por ciertas partículas hace mucho tiempo y lejos. Por ejemplo, tal vez\(o_1\) está en reposo en relación con cierta carga\(q\) que ayudó a crear los campos, pero\(o_2\) no lo es, así que\(o_2\) recoge\(q\) el campo magnético, que es información no disponible para\(o_1\) — quien piensa que\(q\) estaba en reposo, y por lo tanto no hizo ninguna campo magnético. Esto contradiría nuestra hipótesis de “eso es todo lo que hay”.
Para mostrar la potencia de “eso es todo lo que hay”, consideremos el ejemplo 9.1.1, en el que encontramos que impulsar un solenoide a lo largo de su propio eje no cambia su campo interno. Como dato sobre los solenoides, es bastante oscuro e inútil. Pero si los campos deben tener leyes de transformación, entonces hemos aprendido algo mucho más general: un campo magnético siempre permanece igual bajo un impulso en la dirección del campo.


