1.4: Geometría Ordenada

Tratemos de poner lo que hemos aprendido en un contexto geométrico general.

La geometría familiar de Euclides del espacio bidimensional tiene los siguientes axiomas, ⁶ los cuales se expresan en términos de operaciones que se pueden llevar a cabo con una brújula y una recta sin marcar:

• E1 Dos puntos determinan una línea.
• Los segmentos de línea E2 se pueden extender.
• E3 Un círculo único se puede construir dado cualquier punto como su centro y cualquier segmento de línea como su radio.
• E4 Todos los ángulos rectos son iguales entre sí.
• E5 Postulado paralelo: Dada una línea y un punto no en la línea, no se puede dibujar más de una línea a través del punto y paralela a la línea dada. ⁷

Nota

Se trata de una forma conocida como axioma de Playfair, más que la versión del postulado originalmente dada por Euclides.

El estilo moderno en matemáticas es considerar este tipo de sistema axiomático como un sandbox autónomo, con los axiomas, y cualquier teorema demostrado a partir de ellos, siendo verdaderos o falsos sólo en relación entre sí. Euclides y sus contemporáneos, sin embargo, creían que eran hechos empíricos sobre la realidad física. Por ejemplo, consideraron que el quinto postulado era menos obvio que los cuatro primeros, pues para verificar físicamente que dos líneas fueran paralelas, teóricamente uno tendría que extenderlas a una distancia infinita y asegurarse de que nunca se cruzaran. En los primeros 28 teoremas de los Elementos, Euclides se restringe enteramente a proposiciones que pueden probarse a partir de los primeros cuatro postulados más seguros. La geometría más general definida omitiendo el postulado paralelo se conoce como geometría absoluta.

¿Qué tipo de geometría es probable que sea aplicable a la relatividad general? Podemos ver de inmediato que la geometría euclidiana, o incluso la geometría absoluta, sería demasiado especializada. Tenemos en mente la descripción de eventos que son puntos tanto en el espacio como en el tiempo. Confinándonos por facilidad de visualización a una dimensión de espacio, ciertamente podemos construir un plano descrito por coordenadas (t, x), pero imponer los postulados de Euclides en este plano resulta en tonterías físicas. El espacio y el tiempo son físicamente distinguibles entre sí. Pero los postulados 3 y 4 describen una geometría en la que las distancias medidas a lo largo de ejes no paralelos son comparables, y las figuras pueden girarse libremente sin afectar la verdad o falsedad de las afirmaciones sobre ellas; esto solo es apropiado para una descripción física de diferentes direcciones espaciales, como en una (x, y) plano cuyos dos ejes son indistinguibles.

Necesitamos arrojar la mayor parte del aparato especializado de geometría euclidiana por la borda. Una vez que hayamos despojado nuestra geometría al mínimo, entonces podemos regresar y construir un conjunto diferente de equipos que se adapten mejor a la relatividad.

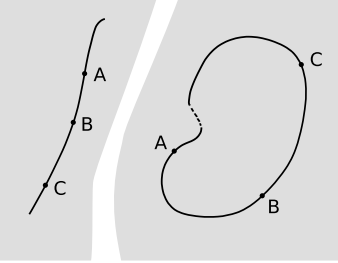
La geometría reducida que queremos se llama geometría ordenada, y fue desarrollada por Moritz Pasch alrededor de 1882. Como sugiere la parábola de Alice y Betty, la geometría ordenada no tiene ningún sistema global de medición que lo abarque todo. Cuando Betty se va de viaje, traza un camino particular a través del espacio de los eventos, y Alice, quedándose en casa, rastrea otro. Si bien los eventos se desarrollan en orden de causa y efecto a lo largo de cada uno de estos caminos, no esperamos poder medir los tiempos a lo largo de los caminos A y B y hacer que salgan de la misma manera. Así es como funciona la geometría ordenada: los puntos se pueden poner en un orden definido a lo largo de cualquier línea en particular, pero no a lo largo de líneas diferentes. De los cuatro conceptos primitivos utilizados en el E1-E5 de Euclides —punto, línea, círculo y ángulo— solo las nociones no métricas de punto (es decir, evento) y línea son relevantes en geometría ordenada. En una geometría sin medición, no existe el concepto de medir la distancia (de ahí que no haya brújulas ni círculos), ni de medir ángulos. La notación [ABC] indica que el evento B se encuentra en un segmento de línea que une A y C, y se encuentra estrictamente entre ellos.

Los axiomas de geometría ordenada son los siguientes: ⁸

• O1 Dos eventos determinan una línea.
• Los segmentos de línea O2 se pueden extender: dados A y B, hay al menos un evento tal que [ABC] es verdadero.
• Las líneas O3 no se envuelven: si [ABC] es verdadero, entonces [BCA] es falso.
• O4 Interweenness: Para cualquiera de tres eventos distintos A, B y C que se encuentran en la misma línea, podemos determinar si B está o no entre A y C (y por la instrucción 3, este orden es único excepto por una posible inversión general para formar [CBA]).

Nota

Figura 1.4.1 - Axiomas O2 (izquierda) y O3 (derecha).

Los axiomas se resumen para una referencia conveniente. Esto pretende ser un resumen informal y legible del sistema, presentado al mismo nivel de holgura que el E1-E5 de Euclides. Los matemáticos modernos han descubierto que sistemas como estos en realidad necesitan bastante más maquinaria técnica para ser perfectamente rigurosos, así que si buscas una axiomatización de geometría ordenada, o una axiomatización moderna de la geometría euclidiana, normalmente encontrarás una lista de axiomas mucho más larga que los presentado aquí. Los axiomas que estoy omitiendo cuidan detalles como asegurarse de que haya más de dos puntos en el universo, y que las curvas no puedan cortarse entre sí sin cruzarse. El libro clásico y bellamente escrito sobre estos temas es la Introducción a la Geometría de H.S.M. Coxeter, que es “introductorio” en el sentido de que es el tipo de libro que una especialización universitaria de matemáticas podría usar en un curso de primera división superior en geometría.

O1-O2 expresan las mismas ideas que el E1-E2 de Euclides. No todas las líneas del sistema corresponderán físicamente a cadenas de causalidad; podríamos tener un segmento lineal que describa una instantánea de una cadena de acero, y O3-O4 entonces decir que el orden de los eslabones está bien definido. Pero O3 y O4 también tienen una clara significación física para las líneas que describen la causalidad. O3 prohíbe las paradojas del viaje en el tiempo, como retroceder en el tiempo y matar a nuestra propia abuela cuando era niña; La figura anterior ilustra por qué una violación de O3 se conoce como una curva cerrada similar al tiempo. O4 dice que se garantiza que los eventos tengan un orden de causa y efecto bien definido solo si se encuentran en la misma línea. Esto es completamente diferente de la actitud expresada en la famosa declaración de Newton: “El tiempo absoluto, verdadero y matemático, de sí mismo, y de su propia naturaleza fluye igual sin tener en cuenta nada externo...”

Si te consterna la austeridad de un sistema de geometría sin ninguna noción de medición, puede que estés más horrorizado al saber que incluso un sistema tan débil como la geometría ordenada hace algunas afirmaciones que son demasiado fuertes para ser completamente correctas como base para la relatividad. Por ejemplo, si un observador cae en un agujero negro, en algún momento llegará a un punto central de densidad infinita, llamado singularidad. En este punto, su cadena de causa y efecto termina, violando\ O2). También es una pregunta abierta si la prohibición de O3 sobre los bucles de tiempo realmente se mantiene en la relatividad general; esta es la conjetura de protección cronológica de Stephen Hawking, llamada juguetonamente. También veremos que en general la relatividad O1 es casi siempre cierta, pero hay excepciones.

Figura 1.4.2 - Stephen Hawking (1942-).