3.6: La Métrica (Parte 1)

Considera una coordenada x definida a lo largo de una determinada curva, que no es necesariamente una geodésica. Para concretar, imaginemos que esta curva existe en dos dimensiones espaciales, las cuales podemos visualizar como la superficie de una esfera incrustada en el espacio 3 euclidiano. Estas características concretas no son estrictamente necesarias, pero conducen a casa el punto que no debemos esperar para poder definir x para que varíe a un ritmo constante con la distancia transcurrida; por ejemplo, sabemos que no será posible definir una cuadrícula cartesiana bidimensional en la superficie de una esfera. En la figura, las marcas de verificación, por lo tanto, no están espaciadas uniformemente. Esto está perfectamente bien, dada la invarianza de coordenadas de la relatividad general. Como los cambios incrementales en x son iguales, los he representado debajo de la curva como pequeños vectores de igual longitud. Tienen la longitud equivocada para representar distancias a lo largo de la curva, pero esta insensatez es un hecho inevitable de la vida en la relatividad.

Figura\(\PageIndex{1}\): Las marcas de verificación en la línea definen una coordenada medida a lo largo de la línea. No es posible establecer dicho sistema de coordenadas globalmente para que la coordenada sea uniforme en todas partes. Las flechas representan cambios en el valor de la coordenada; dado que los cambios en la coordenada son todos iguales, las flechas son todas de la misma longitud.

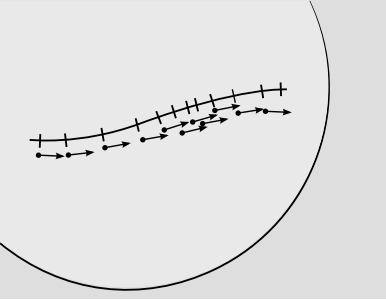
Ahora supongamos que queremos integrar la longitud del arco de un segmento de esta curva. Los pequeños vectores son infinitesimales. En la longitud integrada, cada pequeño vector debe aportar alguna cantidad, que es un escalar. Este escalar no es simplemente la magnitud del vector,\(ds \neq \sqrt{d \textbf{x} \cdot d \textbf{x}}\), ya que los vectores tienen la longitud equivocada. La figura\(\PageIndex{1}\) es claramente una reminiscencia de la imagen geométrica de vectores y vectores duales desarrollados anteriormente. Pero la noción puramente afín de vectores y sus duales no es suficiente para definir la longitud de un vector en general; sólo es suficiente definir una longitud relativa a otras longitudes a lo largo de una misma geodésica. Cuando los vectores se encuentran a lo largo de diferentes geodésicas, necesitamos poder especificar el factor de conversión adicional que nos permita comparar uno con otro. A la pieza de maquinaria que nos permite hacer esto se le llama métrica.

Fijar una métrica nos permite definir el escalado adecuado de las marcas de garrapata en relación con las flechas en un punto dado, es decir, en la notación de las pistas de aves nos da una forma natural de tomar un vector de desplazamiento como →s, con la flecha apuntando hacia el símbolo, y haciendo un vector dual correspondiente s→, con el flecha saliendo. Esto es un poco como clonar a una persona pero hacer que el clon sea del sexo opuesto. Conectarlos como s→s entonces nos dice la magnitud cuadrada del vector. Por ejemplo, si →dx es un desplazamiento infinitesimal parecido al tiempo, entonces dx→dx es el intervalo de tiempo cuadrado dx ² medido por un reloj que viaja a lo largo de ese desplazamiento en el espacio-tiempo. (Tenga en cuenta que en la notación dx ², está claro que dx es un escalar, porque a diferencia de →dx y dx→ no tiene ninguna flecha entrando o saliendo de ella). La figura\(\PageIndex{2}\) muestra la imagen resultante.

Figura\(\PageIndex{2}\): Los vectores →dx y dx→ son duales entre sí.

En la notación de índice abstracto introducida anteriormente, los vectores →dx y dx→ se escriben dx ^a y dx _a. Cuando se ha fijado un sistema de coordenadas específico, los escribimos con concreto, Índices griegos,\(dx^\mu\) y\(dx_{\mu}\). En una notación y terminología más antiguas y conceptualmente incompatibles debido a Sylvester (1853), uno se refiere\(dx_{\mu}\) como un vector contravariante, y\(dx^\mu\) como covariante. La confusa terminología se resume en el Apéndice C.

La suposición de que existe una métrica no es trivial. No hay métrica en el espacio-tiempo galileo, por ejemplo, ya que en el límite c →\(\infty\) las unidades utilizadas para medir desplazamientos similares al tiempo y espaciales no son comparables. Asumir la existencia de una métrica equivale a suponer que el universo contiene al menos un reloj o regla físicamente manipulable que puede moverse a largas distancias y acelerarse según se desee. En un futuro lejano, las regiones grandes y causalmente aisladas del cosmos pueden contener únicamente partículas sin masa como los fotones, que no pueden ser utilizadas para construir relojes (o, equivalentemente, gobernantes); la física de estas regiones será completamente descriptible sin una métrica. Si, por otro lado, nuestro mundo contiene no sólo cero o uno sino dos o más relojes, entonces la hipótesis métrica requiere que estos relojes mantengan una tasa relativa consistente cuando se aceleran a lo largo de la misma línea mundial. Esta consistencia es lo que nos permite pensar en la relatividad como una teoría del espacio y el tiempo más que una teoría de relojes y gobernantes. Existen otras teorías relativistas de la gravedad además de la relatividad general, y algunas de ellas violan esta hipótesis.

Dado un dx ^\(\mu\), ¿cómo encontramos su dx dual _\(\mu\), y viceversa? En una dimensión, simplemente necesitamos introducir un número real g como factor de corrección. Si uno de los vectores es más corto de lo que debería ser en una región determinada, el factor de corrección sirve para compensar haciendo su doble proporcionalmente más largo. Los dos mapeos posibles (covariante a contravariante y contravariante a covariante) se logran con factores de g y 1/g, el número g es la métrica y codifica toda la información sobre distancias. Por ejemplo, si\(\phi\) representa la longitud medida en el círculo ártico, entonces la métrica es la única fuente para el dato que un desplazamiento d\(\phi\) corresponde a 2540 km por radián.

Ahora generalicemos a más de una dimensión. Debido a que los sistemas de coordenadas globalmente cartesianas no pueden imponerse a un espacio curvo, las líneas de coordenadas constantes no estarán generalmente espaciadas ni perpendiculares entre sí. Si construimos un conjunto local de vectores base que se encuentran a lo largo de las intersecciones de las superficies de coordenadas constantes, no formarán un conjunto ortonormal. Nos gustaría tener una expresión de la forma

\[ds^{2} = \sum dx^{\mu} dx_{\mu}\]

para la longitud del arco cuadrado, y usando la notación de suma de Einstein esto se convierte en

\[ds^{2} = dx^{\mu} dx_{\mu}\]

La Métrica Euclidiana

Para las coordenadas cartesianas en un plano euclidiano, donde normalmente no se molesta con la distinción entre vectores covariantes y contravariantes, esta expresión for\(ds^2\) es simplemente el teorema de Pitágoras, sumado sobre dos valores de\(\mu\) para las dos coordenadas:

\[ds^{2} = dx^{\mu} dx_{\mu} = dx^{2} + dy^{2}\]

Los símbolos dx, ds ⁰, dx ⁰ y dx ₀ son todos sinónimos, e igualmente para dy, ds ¹, dx ¹ y dx ₁. (Debido a que notaciones como ds ¹ obligan al lector a realizar un seguimiento de qué dígitos se han asignado a qué letras, es mejor practicar usar notación como dy o ds ^y; esta última notación podría confundirse en principio con una en la que y era una variable que tomaba valores como 0 o 1, pero en realidad lo entendemos desde el contexto, así como entendemos que las d's in no\(\frac{dy}{dx}\) se refieren a alguna variable d que significa un número.)

En el caso no euclidiano, el teorema de Pitágoras es falso;\(dx^\mu\) y ya no\(dx_\mu\) son sinónimos, por lo que su producto ya no es simplemente el cuadrado de una distancia. Para ver esto de manera más explícita, escribamos la expresión para que solo se produzcan las cantidades covariantes. Por planitud local, la relación entre los vectores covariantes y contravariantes es lineal, y la relación más general de este tipo se da haciendo de la métrica una matriz simétrica\(g_{\mu \nu}\). Sustituyendo\(dx_{\mu} = g_{\mu \nu} x^{\nu}\), tenemos

\[ds^{2} = g_{\mu \nu} dx^{\mu} dx^{\nu}\]

donde ahora hay sumas implícitas sobre ambos µ y ν. Observe cómo las sumas implícitas ocurren solo cuando el índice repetido ocurre una vez como superíndice y una vez como subíndice; otras combinaciones son no gramaticales.

Ejercicio\(\PageIndex{1}\)

Autocomprobación: ¿Por qué tiene sentido exigir que la métrica sea simétrica?

Anteriormente encontramos la distinción entre escalares, vectores y vectores duales. Estos son ejemplos específicos de tensores, que se pueden expresar en la notación de las pistas de aves como objetos con m flechas entrando y n saliendo, o. En notación de índice, tenemos m superíndices y n subíndices. Un escalar tiene m = n = 0. Un vector dual tiene (m, n) = (0, 1), un vector (1, 0) y la métrica (0, 2). Nos referimos al número de índices como el rango del tensor. Los tensores se discuten con más detalle, y se definen más rigurosamente, en el capítulo 4. Para nuestros propósitos actuales, es importante señalar que solo porque escribimos un símbolo con subíndices o superíndices, eso no significa que merezca ser llamado tensor. Este punto se puede entender en el contexto más elemental de los escalares y vectores newtonianos. Por ejemplo, podemos definir un “vector” euclidiano u = (m, T, e), donde m es la masa de la luna, T es la temperatura en Chicago, y e es la carga del electrón. Esta criatura u no merece ser llamada vector, porque no se comporta como un vector bajo rotación. La filosofía general es que un tensor es algo que tiene ciertas propiedades bajo cambios de coordenadas. Por ejemplo, ya hemos visto anteriormente el diferente comportamiento de escalado de tensores con rangos (1, 0), (0, 0) y (0, 1).

Al discutir la simetría de los tensores de rango 2, es conveniente introducir la siguiente notación:

\[T_{(ab)} = \frac{1}{2} (T_{ab} + T_{ba})\]

\[T_{[ab]} = \frac{1}{2} (T_{ab} - T_{ba})\]

Cualquier T _ab se puede dividir en partes simétricas y antisimétricas. Esto es similar a escribir una función arbitraria como una función suma de e impar y una función par. La métrica tiene solo una parte simétrica: g _(ab) = g _ab, y g _[ab] = 0. Esta notación se generaliza a rangos mayores a 2 posteriores.

Ejercicio\(\PageIndex{2}\)

Autocomprobación: Caracterizar un tensor antisimétrico rank-2 en dos dimensiones.

Ejemplo 7: Un cambio de escala

• Supongamos que comenzamos describiendo el plano euclidiano con un cierto conjunto de coordenadas cartesianas, pero luego queremos cambiar a un nuevo conjunto de coordenadas que se reescalan en comparación con las originales. ¿Cómo se representa en g el efecto de esta reescalación?.
• Si cambiamos nuestras unidades de medida para que\(x_{\mu} \rightarrow \alpha x^{\mu}\), mientras exigimos que ds ² salga igual, entonces necesitamos\(g_{\mu \nu} \rightarrow \alpha^{−2} g_{\mu \nu}\).

Comparando con la sección 2.1, deducimos la regla general de que un tensor de rango (m, n) se transforma bajo escala recogiendo un factor de\(\alpha^{m−n}\).

Toda esta noción de escalado y unidades en la relatividad general resulta no trivial e interesante. Véase la sección 5.11, para una discusión más detallada.

Ejemplo 8: coordenadas polares

Considera las coordenadas polares (r,\(\theta\)) en un plano euclidiano. Las curvas de coordenada constante son ortogonales en todas partes, por lo que los elementos fuera de la diagonal de la métrica g _{\(\theta\)r\(\theta\) y g r} desaparecen. Los cambios de coordenadas infinitesimales dr y d\(\theta\) corresponden a desplazamientos infinitesimales dr y r d\(\theta\) en direcciones ortogonales, así que por el teorema de Pitágoras, ds ² = dr ² + r\(\theta\) ^{2 d 2}, y leemos los elementos de la métrica g _rr = 1 y g _{\(\theta\)\(\theta\)}= r ².

Observe cómo en el ejemplo 8 partimos de la relación generalmente válida\(ds^{2} = g_{\mu \nu} dx^{\mu} dx^{\nu}\), pero pronto comenzamos a anotar hechos como g _{\(\theta\)\(\theta\)}= r ² que sólo eran válidos en este sistema de coordenadas en particular. Para que quede claro cuando esto sucede, mantenemos la distinción entre índices latinos abstractos e índices griegos concretos introducidos anteriormente. Por ejemplo, podemos escribir la expresión general para longitud de arco diferencial cuadrado con índices latinos,

\[ds^{2} = g_{ij} dx^{i} dx^{j},\]

porque se mantiene independientemente del sistema de coordenadas, mientras que la fuga de los elementos fuera de la diagonal de la métrica en coordenadas polares euclidianas tiene que escribirse como g _{\(\mu \nu\)}= 0 for\(\mu \neq \nu\), ya que en general sería falso si usáramos un sistema de coordenadas diferente para describir el mismo plano euclidiano.

Ejemplo 9: Coordenadas cartesianas oblicuas

Figura\(\PageIndex{3}\)

• Las coordenadas cartesianas oblicuas son como coordenadas cartesianas normales en el plano, pero sus ejes están formando un ángulo\(\phi \neq \frac{\pi}{2}\) entre sí. Encuentra la métrica en estas coordenadas. El espacio es globalmente euclidiano.
• Dado que las coordenadas difieren de las coordenadas cartesianas solo en el ángulo entre los ejes, no en sus escalas, un desplazamiento dx ⁱ a lo largo de cualquiera de los ejes, i = 1 o 2, debe dar ds = dx, así que para los elementos diagonales tenemos g ₁₁ = g ₂₂ = 1. La métrica es siempre simétrica, por lo que g ₁₂ = g ₂₁. Para fijar estos elementos fuera de diagonal, considere un desplazamiento por ds en la dirección perpendicular al eje 1. Esto cambia las coordenadas por dx ¹ = − ds cot\(\phi\) y dx ² = ds cos\(\phi\). Entonces tenemos

\[\begin{split} ds^{2} &= g_{ij} dx^{i} dx^{j} \\ &= ds^{2} (\cot^{2} \phi + csc^{2} \phi - 2g_{12} \cot \phi \csc \phi) \\ g_{12} &= \cos \phi \ldotp \end{split}\]

Ejemplo 10: área

En una dimensión, g es un solo número, y las longitudes vienen dadas por ds =\(\sqrt{g}\) dx. La raíz cuadrada también se puede entender a través del ejemplo 7, en el que vimos que se refleja en un reescalado uniforme\(\alpha\) x → x\(g_{\mu \nu} \rightarrow \alpha^{−2} g_{\mu \nu}\).

En coordenadas cartesianas bidimensionales, la multiplicación del ancho y alto de un rectángulo da el elemento de área\(dA = \sqrt{g_{11} g_{22}} dx^{1} dx^{2}\). Debido a que las coordenadas son ortogonales, g es diagonal, y el factor de\(\sqrt{g_{11} g_{22}}\) se identifica como la raíz cuadrada de su determinante, por lo que dA =\(\sqrt{|g|}\) dx ¹ dx ². Tenga en cuenta que las escalas en los dos ejes no son necesariamente las mismas, g ₁₁ ≠ g ₂₂.

La misma expresión para el elemento de área se mantiene aunque las coordenadas no sean ortogonales. En el ejemplo 9, por ejemplo, tenemos\(\sqrt{|g|} = \sqrt{1 − \cos^{2} \phi} = \sin \phi\), que es el factor de corrección correcto correspondiente al hecho de que dx ¹ y dx ² forman un paralelepípedo en lugar de un rectángulo.

Ejemplo 11: área de una esfera

Para coordenadas\((\theta, \phi)\) en la superficie de una esfera de radio r, tenemos, por un argumento similar al del ejemplo 8\(g_{\theta \theta} = r^{2}, g_{\phi \phi} = r^{2} \sin^{2} \theta, g_{\theta \phi} = 0\). El área de la esfera es

\[\begin{split} A &= \int dA \\ &= \int \int \sqrt{|g|} d \theta d \phi \\ &= r^{2} \int \int \sin \theta d \theta d \phi \\ &= 4 \pi r^{2} \end{split}\]

Ejemplo 12: inverso de la métrica

• Relacionar g ^ij con g _ij.
• La notación pretende tratar vectores covariantes y contravariantes completamente simétricamente. La métrica con índices inferiores g _ij puede interpretarse como una transformación de cambio de base de una base contravariante a una covariante, y si se quiere mantener la simetría de la notación, g ^ij debe ser la matriz inversa correspondiente, que cambia de la base covariante a la uno contravariante. La métrica siempre debe ser invertible.

En el caso unidimensional, la métrica en cualquier punto dado fue simplemente algún número g, y se utilizaron factores de g y 1/g para convertir ida y vuelta entre vectores covariantes y contravariantes. El Ejemplo 12 deja claro cómo generalizar esto a más dimensiones:

\[\begin{split} x_{a} &= g_{ab} x^{b} \\ x^{a} &= g^{ab} x_{b} \end{split}\]

Esto se conoce como índices de subida y bajada. No hay necesidad de memorizar las posiciones de los índices en estas reglas; son las únicas posibles con base en las reglas gramaticales, que son que la suma sólo ocurre sobre pares superior-inferior, y los índices superior e inferior tienen que coincidir en ambos lados del signo igual. Todo este sistema, introducido por Einstein, se llama notación “índice-gimnasia”.

Ejemplo 13: Subir y bajar índices en un tensor de rango dos

En física encontramos diversos ejemplos de matrices, como el momento del tensor de inercia de la mecánica clásica. Estos tienen dos índices, no sólo uno como un vector. Nuevamente, las reglas para subir y bajar índices siguen directamente de la gramática. Por ejemplo,

\[A^{a}_{b} = g^{ac} A_{cb}\]

y

\[A_{ab} = g_{ac} g_{bd} A^{cd} \ldotp\]

Ejemplo 14: Una matriz que opera sobre un vector

Los vectores de fila y columna del álgebra lineal son los vectores covariantes y contravariantes en nuestra terminología actual. (La convención es que los vectores covariantes son vectores de fila y vectores de columna contravariantes, pero no me parece que valga la pena memorizar esto). ¿Qué pasa con las matrices? Una matriz que actúa sobre un vector de columna da otro vector de columna, q = U p Traduciendo esto a notación de indexgymnastics, tenemos

\[q^{a} = U^{\ldots} \ldots p^{b},\]

donde queremos averiguar la correcta colocación de los índices en U. Gramaticalmente, la única colocación posible es

\[q^{a} = U^{a}_{b} p^{b} \ldotp\]

Esto muestra que la forma natural de representar un operador lineal columna-vector-a-columna-vector es como un tensor rank-2 con un índice superior y un índice inferior.

En la notación birdtracks, un tensor rank-2 es algo que tiene dos flechas conectadas a él. Nuestro ejemplo se vuelve → q =→ U → p. Que el resultado es en sí mismo un vector de índice superior se muestra por el hecho de que el lado derecho tomado como un todo tiene una sola flecha externa entrando en él.

La distinción entre vectores y sus duales puede parecer irrelevante si siempre podemos subir y bajar índices a voluntad. No siempre podemos hacer eso, sin embargo, porque en muchas situaciones perfectamente ordinarias no hay métrica. Ver ejemplo 6.

La música de Lorentz

En un espacio localmente euclidiano, el teorema de Pitágoras nos permite expresar la métrica en coordenadas cartesianas locales en forma simple

\[g_\mu\mu = +1, g\mu\nu = 0\]

es decir,

\[g = diag(+1, +1, . . . , +1).\]

Esta no es la métrica apropiada para un espacio local de Lorentz. Los axiomas de la geometría euclidiana E3 (existencia de círculos) y E4 (igualdad de ángulos rectos) describen la invarianza de la teoría bajo rotaciones, y el teorema de Pitágoras es consistente con esto, porque da la misma respuesta para la longitud de un vector aunque sus componentes se reexpresen en una nueva base que se gira con respecto al original. En una geometría lorentziana, sin embargo, nos importa la invarianza bajo refuerzos de Lorentz, que no preservan la cantidad\(t^2 + x^2\). No son los círculos en el plano (t, x) los que son invariantes, sino los conos ligeros, y esto se describe dando g _tt y g _xx signos opuestos e iguales valores absolutos. Un vector similar a la luz (t, x), con t = x, por lo tanto tiene una magnitud de exactamente cero

\[s^{2} = g_{tt} t^{2} + g_{xx} x^{2} = 0,\]

y esto sigue siendo cierto después del impulso de Lorentz (t, x) → (\(\gamma\)t,\(\gamma\) x). Es cuestión de convención qué elemento de la métrica hacer positivo y cuál hacer negativo. En este libro, usaré g _tt = +1 y g _xx = −1, de modo que g = diag (+1, −1). Esto tiene la ventaja de que cualquier segmento de línea que represente la línea mundial similar al tiempo de un objeto físico tiene una magnitud cuadrada positiva; el flujo directo del tiempo se representa como un número positivo, de acuerdo con la filosofía de que la relatividad es básicamente una teoría de cómo funcionan las relaciones causales. Con esta convención de signos, los vectores espaciales tienen magnitudes cuadradas positivas, las temporales negativas. A la misma convención le sigue, por ejemplo, Penrose. La versión opuesta, con g = diag (−1, +1) es utilizada por autores como Wald y Misner, Thorne y Wheeler.

Nuestro universo no tiene una sola dimensión espacial, tiene tres, por lo que la métrica completa en un marco Lorentz viene dada por

\[g = diag(+1, −1, −1, −1).\]

Ejemplo 15: Forma mixta covariante-contravariante de la métrica

En el ejemplo 13, vimos cómo subir y bajar índices en un tensor de rango dos, y el ejemplo 14 mostró que a veces es natural considerar la forma en que se eleva un índice y se baja uno. La métrica en sí es un tensor de rango dos, así que veamos qué sucede cuando calculamos la forma mixta g a _b ^a partir de la forma de índice inferior. En general, tenemos

\[A^{a}_{b} = g^{ac} A_{cb},\]

y sustituyendo g por A da

\[g_{b}^{a} = g^{ac} g_{cb} \ldotp\]

Pero ya sabemos que g^... es simplemente la matriz inversa de g_... (ejemplo 12), lo que significa que g ^a _b es simplemente la matriz de identidad. ^{Es decir, mientras que una cantidad como g _ab o g ab lleva toda la información sobre nuestro sistema de medición en un punto dado, g a _b no lleva ninguna información. Donde g _ab o g ab pueden tener tanto elementos positivos como negativos, elementos que tienen unidades y elementos fuera de diagonal, g a _b es solo un símbolo genérico que no contiene información que no sea la dimensionalidad del espacio.}

El tensor métrico es de uso tan común que simplemente se deja fuera de los diagramas de oruga. La consistencia se mantiene porque porque g ^a _b es la matriz de identidad, entonces → g → es lo mismo que →→.