4.6: Leyes de conservación

No hay leyes generales de conservación

Algunos de los primeros tensores que discutimos fueron masa y carga, ambos tensores de rango 0, y el tensor de impulso rank-1, que contiene tanto la energía clásica como el impulso clásico. Los físicos originalmente decidieron que la masa, la carga, la energía y el impulso eran interesantes porque se encontró que estas cosas estaban conservadas. Esto hace que sea natural preguntarse cómo se pueden formular las leyes de conservación en la relatividad. Estamos acostumbrados a declarar las leyes de conservación casualmente en términos de la cantidad de algo en todo el universo, por ejemplo, que clásicamente la cantidad total de masa en el universo permanece constante. La relatividad sí nos permite hacer modelos físicos del universo en su conjunto, por lo que parece que debemos poder hablar de leyes de conservación en la relatividad.

No podemos.

Primero, ¿cómo definimos “se mantiene constante”? La simultaneidad no está bien definida, así que no podemos simplemente tomar dos instantáneas, llamarlas inicial y final, y comparar la cantidad total de, digamos, carga eléctrica en cada instantánea. Esta dificultad no es insuperable. Como en la figura a, podemos seleccionar arbitrariamente superficies tridimensionales en forma de espacio —una inicial y otra final— e integrar la carga sobre cada una. Una ley de conservación de la carga diría que no importa qué superficie espacial escojamos, la carga total en cada una sería la misma.

Figura\(\PageIndex{1}\) - Dos superficies espaciosas.

A continuación está la cuestión de que la integral podría divergir, sobre todo si el universo era espacialmente infinito. Por ahora, supongamos un universo espacialmente finito. Por simplicidad, supongamos que tiene la topología de una tres esferas (ver sección 8.2 para asegurar que esto no es físicamente irrazonable), y podemos visualizarla como una esfera de dos.

Figura\(\PageIndex{2}\) - Definimos un límite alrededor de una región cuya carga queremos medir.

En el caso del momentum four vector, ¿en qué sistema de coordenadas lo expresaríamos? En general, ni siquiera esperamos poder definir un sistema de coordenadas suave y de buen comportamiento que abarque todo el universo, e incluso si lo hiciéramos, no tendría sentido agregar un vector expresado en ese sistema de coordenadas en el punto A a otro vector del punto B; lo mejor que podríamos hacer sería paralelamente- transportar los vectores a un punto y luego agregarlos, pero el transporte paralelo depende de la ruta. (Problemas similares ocurren con el momento angular). Por ello, limitémonos al caso más fácil de un escalar, como es la carga eléctrica.

Figura\(\PageIndex{3}\) - Este límite corta la esfera en partes iguales.

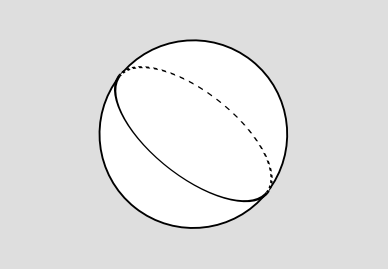
Pero ahora estamos en verdaderos problemas. ¿Cómo íbamos a medir realmente la carga eléctrica total del universo? La única manera de hacerlo es medir los campos eléctricos, y luego aplicar la ley de Gauss. Esto requiere que destaquemos alguna superficie sobre la que podamos integrar el flujo, como en la Figura 4.5.2. Esto realmente sería una superficie bidimensional en la tres esfera, pero podemos visualizarla como una superficie unidimensional —una curva cerrada— en la biesfera. Pero ahora supongamos que esta curva es un gran círculo, Figura 4.5.3. Si medimos un flujo total que no se desvanece a través de él, ¿cómo sabemos dónde está la carga? Podría ser de cualquier lado.

La conclusión es que las leyes de conservación solo tienen sentido en la relatividad en circunstancias muy especiales. ¹⁶ No tenemos nada como principios generales, globales de conservación. Como ejemplo de las circunstancias especiales apropiadas, la sección 6.2 muestra cómo definir las cantidades conservadas, que se comportan como energía e impulso, para el movimiento de una partícula de prueba en una métrica particular que tiene cierta simetría. Esto se generaliza en la sección 7.1 a una ley de conservación general y global correspondiente a toda simetría continua de un espacio-tiempo.

Nota

Para otro argumento que lleva a la misma conclusión, véase la sección 7.5.

Conservación de Momentum Angular y Arrastrado de Marco

Otro caso especial en el que funcionan las leyes de conservación es que si el espacio-tiempo que estamos estudiando se vuelve muy plano a grandes distancias de un sistema pequeño que estamos estudiando, entonces podemos definir un límite lejano que rodea al sistema, medir el flujo a través de ese límite y encontrar la carga del sistema. Para tal planitud asintótica espacio-tiempos, también podemos sortear los problemas que surgen con vectores conservados, como el momentum. (La planitud asintótica se discute con más detalle en la sección 7.4.) Si el espacio-tiempo lejano es casi plano, entonces el transporte paralelo pierde su dependencia de ruta, por lo que podemos definir sin ambigüedades una noción de transportar en paralelo todas las contribuciones al flujo a un punto P arbitrariamente elegido y luego agregarlas. La planitud asintótica también nos permite definir una noción aproximada de un marco global de Lorentz, de manera que la elección de P no importa.

A modo de ejemplo, la Figura 4.5.4 muestra un chorro de materia que es expulsado de la galaxia M87 en campos ultrarelativistas. El color azul del chorro en la imagen de luz visible proviene de la radiación sincrotrón, que es la radiación electromagnética emitida por partículas cargadas relativistas aceleradas por un campo magnético. Se cree que el jet proviene de un agujero negro supermasivo en el centro de M87. La emisión del chorro en una dirección particular sugiere que el agujero negro no es esféricamente simétrico. Parece tener un eje particular asociado a él. ¿Cómo puede ser esto? La simetría esférica de nuestro sol se rompe por la existencia de características observables externamente como las manchas solares y el bulto ecuatorial, pero la única información que podemos obtener sobre un agujero negro proviene de sus campos gravitacionales externos (y posiblemente electromagnéticos). Parece que algo sobre la métrica espacio-tiempo que rodea este agujero negro rompe la simetría esférica, pero conserva la simetría alrededor de algún eje preferido. ¿Qué aspecto de las condiciones iniciales en la formación del agujero podría haber determinado tal eje? El candidato más probable es el momento angular. Por lo tanto, se nos lleva a sospechar que los agujeros negros pueden poseer impulso angular, que el momento angular conserva información sobre su formación y que el momento angular es externamente detectable a través de su efecto en la métrica espacio-tiempo.

Figura\(\PageIndex{4}\) - Un chorro relativista.

¿Cuál sería la forma de tal métrica? Las coordenadas esféricas en espacio-tiempo plano dan una métrica como esta:

\[ds^{2} = dt^{2} - dr^{2} - r^{2} d \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2} \ldotp\]

Veremos en el capítulo 6 que para un agujero negro no giratorio, la métrica es de la forma

\[ds^{2} = (\ldots) dt^{2} - (\ldots) dr^{2} - r^{2} d \theta^{2} - r^{2} \sin^{2} \theta d \phi^{2},\]

donde (...) representa funciones de r. De hecho, no hay nada especial en la métrica de un agujero negro, al menos lejos; la misma métrica externa se aplica a cualquier cuerpo esféricamente simétrico, no giratorio, como la luna. Ahora, ¿qué pasa con la métrica de un cuerpo giratorio? Esperamos que tenga las siguientes propiedades:

1. Tiene términos que son impares bajo inversión de tiempo, correspondientes a la inversión del momento angular del cuerpo.
2. De igual manera, tiene términos que son impares bajo inversión del diferencial d\(\phi\) de la coordenada acimutal.
3. La métrica debe tener simetría axial, es decir, debe ser independiente de\(\phi\).

Restringiendo nuestra atención al plano ecuatorial\(\theta = \frac{\pi}{2}\), la modificación más simple que tiene estas tres propiedades es agregar un término de la forma

\[f(\ldots) L d \phi dt,\]

donde (...) vuelve a dar la r-dependencia y L es una constante, interpretada como el momento angular. Un tratamiento detallado está fuera del alcance de este libro, pero las soluciones de esta forma a las ecuaciones de campo relativistas fueron encontradas por el físico nacido en Nueva Zelandez Roy Kerr en 1963 en la Universidad de Texas en Austin.

El modelado astrofísico de observaciones como la figura d es complicado, pero podemos ver en un experimento de pensamiento simplificado que si queremos determinar el momento angular de un cuerpo giratorio a través de su campo gravitacional, será difícil a menos que utilicemos un proceso de medición que aproveche la asintótica planitud del espacio. Por ejemplo, supongamos que enviamos dos haces de luz más allá de la tierra, en su plano ecuatorial, uno a cada lado, y medimos sus deflexiones, e. Las deflexiones serán diferentes, porque el signo de d\(\phi\) dt será opuesto para los dos haces. Pero toda la noción de una “desviación” sólo tiene sentido si tenemos un fondo asintóticamente plano, como lo indican las líneas tangentes discontinuas. Además, si el espacio-tiempo no fuera asintóticamente plano en este ejemplo, entonces podría no haber una manera inequívoca de determinar si la asimetría se debió a la rotación de la tierra, a algún factor externo, o a algún tipo de interacción entre la tierra y otros cuerpos cercanos.

Figura\(\PageIndex{5}\) - Dos rayos de luz viajan en el plano ecuatorial de la Tierra de A a B. Debido al arrastre del marco, el rayo que se mueve con la rotación de la tierra se desvía en una cantidad mayor que el que se mueve en contra de él. Como resultado, la figura tiene una forma asimétrica de plátano. Tanto la deflexión como su asimetría son muy exageradas.

También resulta que un giroscopio en tal campo gravitacional precede. Este efecto, llamado arrastre de fotogramas, fue predicho por Lense y Thirring en 1918, y finalmente se verificó experimentalmente en 2008 mediante el análisis de datos del experimento Gravity Probe B, con una precisión de aproximadamente 15%. El experimento se organizó de manera que el efecto geodésico relativamente fuerte (6.6 arco-segundos al año) y el mucho más débil efecto Lense-Thirring (.041 arco-seg/año) produjeron precesiones en direcciones perpendiculares. Nuevamente, se involucró la presencia de un fondo asintóticamente plano, debido a que la sonda midió las orientaciones de sus giroscopios respecto a la estrella guía IM Pegasi.

Figura\(\PageIndex{6 }\) - La sonda de gravedad B verificó la existencia de arrastre de marco. El eje de rotación del giroscopio precede en dos planos perpendiculares debido a los dos efectos separados: geodésico y arrastre de marco.