5.4: Curvatura en Dos Dimensiones Espaciales

Dado que los tensores de curvatura en 3+1 dimensiones son complicados, comencemos considerando dimensiones más bajas. En una dimensión, Figura 5.3.1, no existe la curvatura intrínseca. Esto se debe a que la curvatura describe el fracaso del paralelismo para comportarse como en E5, pero no hay noción de paralelismo en una dimensión.

Figura\(\PageIndex{1}\) - Esta curva no tiene curvatura intrínseca.

La dimensión más baja interesante es, por lo tanto, dos, y este caso fue estudiado por Carl Friedrich Gauss a principios del siglo XIX. Gauss realizó un levantamiento geodésico del estado de Hannover, inventando un instrumento de topografía óptica llamado heliotropo que en efecto se utilizó para cubrir la superficie de la Tierra con una malla triangular de rayos de luz. Si uno de los puntos de malla se encuentra, por ejemplo, en la cima de una montaña, entonces la suma\(\Sigma \theta\) de los ángulos de los vértices que se encuentran en ese punto será menor a 2\(\pi\), en contradicción con Euclides. Si bien los rayos de luz sí viajan por el aire por encima de la tierra, podemos pensarlos como aproximaciones a geodésicas pintadas directamente sobre la suciedad, lo que sería intrínseco más que extrínseco. El defecto angular alrededor de un vértice ahora se desvanece, porque el espacio es localmente euclidiana, pero ahora recogemos un tipo diferente de defecto angular, que es que los ángulos interiores de un triángulo ya no suman al valor euclídeo de\(\pi\).

Figura\(\PageIndex{2}\) - Un topógrafo en la cima de una montaña usa un heliotropo.

Figura\(\PageIndex{3}\) - Un mapa de una encuesta de triangulación como la que Gauss realizó. Al medir los ángulos interiores de los triángulos, se puede determinar no solo la proyección bidimensional de la cuadrícula sino su forma tridimensional completa, incluyendo tanto la curvatura de la tierra (nótese la curvatura de las líneas de latitud) como la altura de las características por encima y por debajo del nivel del mar.

Ejemplo 1: Un levantamiento poligonal de un balón de fútbol

La Figura 5.3.3 aplica ideas similares a un balón de fútbol, siendo la única diferencia el uso de pentágonos y hexágonos en lugar de triángulos.

Figura\(\PageIndex{4}\)

En la Figura 5.3.4 (1), el levantamiento es extrínseco, debido a que las líneas pasan por debajo de la superficie de la esfera. La curvatura es detectable porque los ángulos en cada vértice suman 120 + 120 + 110 = 350 grados, dando un defecto angular de 10 grados.

En la Figura 5.3.4 (2), las líneas se han proyectado para formar arcos de grandes círculos sobre la superficie de la esfera. Debido a que el espacio es localmente euclidiano, la suma de los ángulos en un vértice tiene su valor euclidiano de 360 grados. La curvatura se puede detectar, sin embargo, porque la suma de los ángulos internos de un polígono es mayor que el valor euclidiano. Por ejemplo, cada hexágono esférico da una suma de 6 × 124.31 grados, en lugar del euclidiano 6 × 120. El defecto angular de 6 × 4.31 grados es una medida intrínseca de curvatura.

Ejemplo 2: Defecto angular en la superficie terrestre

Divida el hemisferio norte de la Tierra en cuatro octantes, con sus límites recorriendo el polo norte. Estos octantes tienen lados que son geodésicos, por lo que son triángulos equiláteros. Asumiendo geometría euclidiana, los ángulos interiores de un triángulo equilátero son cada uno igual a 60 grados, y, como con cualquier triángulo, suman 180 grados. El octante-triángulo en la Figura 5.3.5 tiene ángulos que son cada uno de 90 grados, y la suma es 270. Esto demuestra que la superficie de la Tierra tiene una curvatura intrínseca.

Figura\(\PageIndex{5}\)

Este ejemplo sugiere otra forma de medir la curvatura intrínseca, en términos de la relación entre\(\frac{C}{r}\) la circunferencia de un círculo y su radio. En geometría euclidiana, esta relación es igual a 2\(\pi\). Dejar\(\rho\) ser el radio de la Tierra, y considerar el ecuador como un círculo centrado en el polo norte, de manera que su radio sea la longitud de uno de los lados del triángulo en la Figura 5.3.5,\(r = (\frac{\pi}{2}) \rho\). (No confunda r, que es intrínseco, con\(\rho\), el radio de la esfera, que es extrínseco y no igual a r.) Entonces la relación\(\frac{C}{r}\) es igual a 4, que es menor que el valor euclidiano de 2\(\pi\).

Let

\[\epsilon = \sum \theta − \pi\]

ser el defecto angular de un triángulo, y por concreción dejar que el triángulo esté en un espacio con una geometría elíptica, para que tenga una curvatura constante y pueda modelarse como una esfera de radio\(\rho\), con puntos antípodos identificados.

Ejercicio\(\PageIndex{1}\)

En geometría elíptica, ¿cuál es el valor mínimo posible de la cantidad\(\frac{C}{r}\) discutida en el ejemplo 2? ¿En qué se diferencia esto del caso de la geometría esférica?

Queremos una medida de curvatura que sea local, pero si nuestro espacio es localmente plano, debemos tener\(\epsilon → 0\) ya que el tamaño de los triángulos se acerca a cero. Es por ello que la geometría euclidiana es una buena aproximación para mapas de la tierra a pequeña escala. La naturaleza discreta de la malla triangular es solo un artefacto de la definición, por lo que queremos una medida de curvatura que, a diferencia\(\epsilon\), se acerque a algún límite finito a medida que la escala de los triángulos se acerca a cero. ¿Deberíamos esperar que esta escala vaya como\(\epsilon \propto \rho\)? \(\rho^{2}\)? Determinemos el escalado. Primero probamos un lema clásico de Gauss, relativo a una versión ligeramente diferente del defecto angular, para un solo triángulo.

Teorema

En geometría elíptica, el defecto angular\(\epsilon = \alpha + \beta + \gamma − \pi\) de un triángulo es proporcional a su área A.

prueba

Por axioma E2, extender cada lado del triángulo para formar una línea, Figura 5.3.6 (1). Cada par de líneas cruza en un solo punto (E1) y divide el plano en dos lunes con sus cuatro vértices tocando en este punto, Figura 5.3.6 (2). De los seis lunes, nos enfocamos en los tres sombreados, que se superponen al triángulo. En cada uno de estos, los dos ángulos interiores en el vértice son los mismos (Euclides I.15). El área de una lune es proporcional a su ángulo interior, como se desprende de la disección a lunes más estrecho; ya que una lune con un ángulo interior de\(\pi\) cubre toda el área P del plano, la constante de proporcionalidad es\(\frac{P}{\pi}\). La suma de las áreas de los tres lunes es\((\frac{P}{\pi})(\alpha + \beta + \gamma)\), pero estas tres áreas también cubren todo el plano, superponiéndose tres veces en el triángulo dado, y por lo tanto su suma también es igual\(P + 2A\). Equiparar las dos expresiones conduce al resultado deseado.

Figura\(\PageIndex{6}\) - Prueba de que el defecto angular de un triángulo en geometría elíptica es proporcional a su área. Cada círculo blanco representa todo el plano elíptico. La línea discontinua en el borde no es realmente un límite; las líneas que salen del borde simplemente se envuelven. En el modelo esférico, el círculo blanco corresponde a un hemisferio, el cual se identifica con el hemisferio opuesto.

Este cálculo fue puramente intrínseco, ya que no hizo uso de ningún modelo o coordenadas. Por lo tanto, podemos construir una medida de curvatura que podemos estar seguros que es intrínseca,\(K = \frac{\epsilon}{A}\). Esto se llama curvatura gaussiana, y en geometría elíptica es constante en lugar de variar de punto a punto. En el modelo sobre una esfera de radio\(\rho\), tenemos

\[K = \frac{1}{\rho^{2}}.\]

Ejercicio\(\PageIndex{2}\)

Autocomprobación: Verifica la ecuación\(K = \frac{1}{\rho^{2}}\) considerando un triángulo que cubre un octante de la esfera, como en el ejemplo 2.

Coordenadas normales gaussianas

Es útil introducir coordenadas normales o gaussianas, definidas de la siguiente manera. A través del punto O, construya geodésicas perpendiculares y defina las coordenadas afines x e y a lo largo de estas. Para cualquier punto P fuera del eje, defina coordenadas construyendo las líneas a través de P que crucen los ejes perpendicularmente. Para P en un vecindario suficientemente pequeño de O, estas líneas existen y están determinadas de manera única. Las coordenadas polares gaussianas se pueden definir de manera similar.

Figura\(\PageIndex{7}\) - Coordenadas normales gaussianas en una esfera.

Aquí hay dos interpretaciones útiles de K.

1. La curvatura gaussiana mide el fracaso del paralelismo en el siguiente sentido. Que la línea\(\ell\) se construya de manera que cruce el eje y normal en (0, dy) en un ángulo que difiera de la perpendicular por la cantidad infinitesimal d\(\alpha\) (Figura 5.3.8). Construye la línea x' = dx, y deja que d\(\alpha'\) sea el ángulo con el que se forma su perpendicular\(\ell\). Entonces ¹ la curvatura gaussiana en O es $$K =\ frac {d^ {2}\ alpha} {dx dy}, $$donde\(d^{2} \alpha = d \alpha' - d \alpha\).

Figura\(\PageIndex{8}\) - 1. La curvatura gaussiana puede interpretarse como el fracaso del paralelismo representado por\(\frac{d^{2} \alpha}{dx dy}\).

Prueba

Dado que dos líneas cualesquiera se cruzan en geometría elíptica,\(\ell\) cruza el eje x. El corolario sigue entonces por aplicación de la definición de la curvatura gaussiana a los triángulos rectos formados por\(\ell\), el eje x, y las líneas en x = 0 y x = dx, de manera que\(K = \frac{d \epsilon}{dA} = \frac{d^{2} \alpha}{dx dy}\), donde se han descartado terceras potencias de infinitesimales.

2. Desde un punto P, emitir un abanico de rayos en ángulos llenando cierto rango\(\theta\) de ángulos en coordenadas polares gaussianas (Figura 5.3.9). Deje que la longitud del arco de este ventilador en r sea L, que puede no ser igual a su valor euclidiano L _E = r\(\theta\). Entonces ² $$K = -3\ frac {d^ {2}} {dr^ {2}}\ izquierda (\ dfrac {L} {L_ {E}}\ derecha)\ ldotp$$

Figura\(\PageIndex{9}\) - 2. Curvatura gaussiana como L ≠ r\(\theta\).

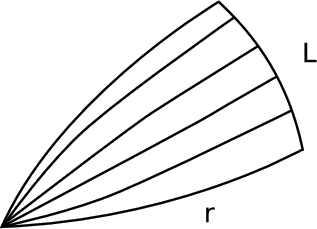
Nota

En el modelo esférico, L =\(\rho \theta\) sin u, donde u es el ángulo subtendido en el centro de la esfera por un arco de longitud r. entonces tenemos\(\frac{L}{L_{E}} = \frac{\sin u}{u}\), cuya segunda derivada con respecto a u es\(- \frac{1}{3}\). Dado que r =\(\rho\) u, la segunda derivada de la misma cantidad con respecto a r es igual\(− \frac{1}{3 \rho^{2}} = − \frac{K}{3}\).

Ahora generalicemos más allá de la geometría elíptica. Considera un espacio modelado por una superficie incrustada en tres dimensiones, con geodésicas definidas como curvas de longitud extrema, es decir, las curvas hechas por un trozo de cuerda tensado a través de la superficie. En un punto P en particular, siempre podemos elegir un sistema de coordenadas (x, y, z) tal que la superficie se aproxime\(z = \frac{1}{2} k_{1} x^{2} + \frac{1}{2} k_{2} y^{2}\) localmente a la superficie al nivel de precisión necesario para discutir la curvatura. La superficie es paraboloidal o hiperboloidal (un sillín), dependiendo de los signos de k ₁ y k ₂. Podríamos pensar ingenuamente que k ₁ y k ₂ podrían determinarse independientemente por mediciones intrínsecas, pero como hemos visto en el ejemplo 5, un cilindro es localmente indistinguible de un plano euclidiano, por lo que si una k es cero, la otra k claramente no se puede determinar. De hecho todo lo que se puede medir es la curvatura gaussiana, que equivale al producto k ₁ k ₂. Para ver por qué esto debería ser cierto, primero considere que cualquier medida de curvatura tiene unidades de distancia inversa al cuadrado, y las k tienen unidades de distancia inversa. Las únicas medidas intrínsecas posibles de curvatura basadas en las k son, por lo tanto, k ² ₁ +k ² ₂ y k ₁ k ₂. (No podemos tener, por ejemplo, solo k ² ₁, porque eso cambiaría bajo una rotación extrínseca alrededor del eje z.) Solo k ₁ k ₂ desaparece en un cilindro, por lo que es la única curvatura intrínseca posible.

Ejemplo 3: Comer pizza

Cuando la gente come pizza doblando la rebanada longitudinalmente, están aprovechando la naturaleza intrínseca de la curvatura gaussiana. Una vez que k ₁ se fija a un valor distinto de cero, k ₂ no puede cambiar sin variar K, por lo que el segmento no puede caer.

Ejemplo 4: Geometría elíptica e hiperbólica

Hemos visto que las figuras que se comportan de acuerdo con los axiomas de geometría elíptica se pueden modelar en parte de una esfera, que es una superficie de constante K > 0. El modelo se puede convertir en uno global satisfaciendo todos los axiomas si se aseguran las propiedades topológicas apropiadas identificando puntos antípodas. Una superficie paraboloidal z = k ₁ x ² + k ₂ y ² puede ser una buena aproximación local a una esfera, pero para puntos alejados de su ápice, K varía significativamente. La geometría elíptica no tiene paralelos; todas las líneas se encuentran si se extienden lo suficiente.

Un espacio de curvatura negativa constante tiene una geometría llamada hiperbólica, y es de cierto interés porque parece ser el que describe las dimensiones espaciales de nuestro universo a escala cosmológica. Una superficie hiperboloidal funciona localmente como modelo, pero su curvatura es aproximadamente constante; la superficie de curvatura constante es una superficie en forma de cuerno creada al girar una curva en forma de montaña llamada tractrix alrededor de su eje. El tractrix de revolución no es un modelo tan satisfactorio como lo es la esfera para geometría elíptica, porque las líneas se cortan en la cúspide de la bocina. La geometría hiperbólica es más rica en paralelismos que la geometría euclidiana; dada una línea\(\ell\) y un punto P no encendido\(\ell\), hay infinitamente muchas líneas a través de P que no pasan\(\ell\).

Figura\(\PageIndex{10}\) - Un triángulo en un espacio con curvatura negativa tiene ángulos que se suman a menos de\(\pi\).

Ejemplo 5: Una pulga en una pelota de fútbol

Podríamos imaginar que una pulga en la superficie de un balompié americano podría determinar por mediciones intrínsecas y locales qué dirección ir para llegar a la punta más cercana. Esto es imposible, porque la pulga tendría que determinar un vector, y la curvatura no puede ser un vector, ya que\(z = \frac{1}{2} k_{1} x^{2} + \frac{1}{2} k_{2} y^{2}\) es invariante bajo la inversión de paridad x → −x, y → −y Por razones similares, una medida de curvatura nunca puede tener un rango impar.

Sin violar la simetría de reflexión, aún es concebible que la pulga pueda determinar la orientación de la línea punta a punta que recorre su posición. Sorprendentemente, incluso esto es imposible. La pulga sólo puede medir el único número K, que no lleva información sobre las direcciones en el espacio.

Figura\(\PageIndex{11}\) - Una pulga en el fútbol no puede orientarse por mediciones intrínsecas y locales.

Ejemplo 6: El pararrayos

Supongamos que tiene un conductor en forma de pera como el de la Figura 5.3.12 (1). Dado que la pera es conductora, hay cargos gratuitos en todas partes dentro de ella. Los paneles 1 y 2 de la figura muestran una simulación por computadora con 100 cargas eléctricas idénticas. En 1, las cargas son liberadas en posiciones aleatorias dentro de la pera. La repulsión hace que todos vuelen hacia la superficie y luego se asienten en un patrón ordenado pero no uniforme.

Figura_5.3.12b.png” />

Figura\(\PageIndex{12}\) - En 1 y 2, las cargas que son visibles en la superficie frontal del conductor se muestran como puntos sólidos; las otras tendrían que verse a través del conductor, que imaginamos es semitransparente.

Puede que no hayamos podido adivinar el patrón de antemano, pero podemos verificar que algunas de sus características tienen sentido. Por ejemplo, el cargo A tiene más vecinos a la derecha que a la izquierda, lo que tendería a hacer que se acelere hacia la izquierda. Pero cuando miramos la imagen en su conjunto, parece razonable que esto se impida por el mayor número de cargas más distantes a su izquierda que a su derecha.

También parece haber un patrón a la no uniformidad: las cargas se acumulan más densamente en áreas como B, donde la curvatura gaussiana es grande, y menos densamente en áreas como C, donde K es casi cero (ligeramente negativa).

Para entender la razón de este patrón, considere la Figura 5.3.12 (3). Es sencillo demostrar que la densidad de carga\(\sigma\) en cada esfera es inversamente proporcional a su radio, o proporcional a K ^1/2. Lord Kelvin demostró que en un elipsoide conductor, la densidad de carga es proporcional a la distancia desde el centro hasta el plano tangente, lo que equivale a ³ a\(\sigma \propto\) K ^1/4; este resultado se ve similar excepto por el diferente exponente. McAllister demostró en 1990 ⁴ que este comportamiento de K ^1/4 se aplica a cierta clase de ejemplos, pero claramente no puede aplicarse en todos los casos, ya que, por ejemplo, K podría ser negativo, o podríamos tener una concavidad profunda, que formaría una jaula de Faraday. El problema 1 discute el caso de un filo de cuchilla.

Razonamiento similar muestra por qué Benjamin Franklin utilizó una punta afilada cuando inventó el pararrayos. Las nubes de tormenta cargadas inducen cargas positivas y negativas para moverse hacia los extremos opuestos de la varilla. En el extremo superior puntiagudo de la varilla, la carga tiende a concentrarse en el punto, y esta carga atrae al rayo. El mismo efecto a veces se puede ver cuando un trozo de papel de aluminio se pone inadvertidamente en un horno de microondas. Experimentos modernos ⁵ muestran que aunque una punta afilada es mejor para iniciar una chispa, una curva más moderada, como la punta derecha de la pera en este ejemplo, es mejor para sostener con éxito la chispa durante el tiempo suficiente para conectar una descarga a las nubes.

---

³ http://math.stackexchange.com/questi...f-the-distance

4 I W McAllister 1990 J. Phys. D: Appl. Phys. 23 359

⁵ Moore et al., Revista de Meteorología Aplicada 39 (1999) 593