5.12: Colectores (Parte 2)

Definición de coordenadas locales de un colector

Una forma alternativa de caracterizar un colector n es como un objeto que puede describirse localmente por n coordenadas reales. Es decir, cualquier vecindario suficientemente pequeño es homeomórfico a un conjunto abierto en el espacio de n-tuplas de valor real de la forma (x ₁, x ₂,., x _n). Por ejemplo, un semiplano cerrado no es un 2-manifold porque ninguna vecindad de un punto en su borde es homeomórfica a ningún conjunto abierto en el plano cartesiano.

Ejercicio\(\PageIndex{1}\)

Autocomprobación: Verifique que esta definición alternativa de colector dé las mismas respuestas que M1-M3 en todos los ejemplos anteriores.

En términos generales, la equivalencia de las dos definiciones ocurre porque estamos usando n números reales como coordenadas para las dimensiones especificadas por M1, y los números reales son el sistema numérico único que tiene las operaciones aritméticas habituales, está ordenado y está completo en el sentido de M3.

Como es habitual cuando decimos que algo es “local”, surge la pregunta de qué tan local es lo suficientemente local. El lenguaje en la definición anterior sobre “cualquier vecindario suficientemente pequeño” es lógicamente similar al\(\epsilon - \delta\) enfoque de Weierstrass: si Alice le da a Bob un colector y un punto en un colector, Bob siempre puede encontrar algún vecindario alrededor de ese punto que sea compatible con las coordenadas, pero puede ser un barrio extremadamente pequeño.

Ejemplo 20: Coordenadas en un círculo

Si vamos a definir coordenadas en un círculo, deben ser funciones continuas. El ángulo\(\phi\) alrededor del centro por lo tanto no funciona del todo como una coordenada global, porque tiene una discontinuidad donde\(\phi\) = 0 se identifica con\(\phi = 2 \pi\). Podemos sortear esto usando diferentes coordenadas en diferentes regiones, como se garantiza que sea posible por la definición de coordenadas locales de un colector. Por ejemplo, podemos cubrir el círculo con dos conjuntos abiertos, uno a la izquierda y otro a la derecha. El izquierdo, L, se define eliminando solo el punto\(\phi\) = 0 del círculo. El correcto, R, se define eliminando solo el uno en\(\phi = \pi\). En L, utilizamos coordenadas\(0 < \phi_{L} < 2 \pi\), que son siempre una función continua desde L hasta los números reales. En R, usamos\(− \pi < \phi_{R} < \pi\).

En ejemplos como este, los conjuntos como L y R se denominan parches. Requerimos que los mapas de coordenadas en los diferentes parches coincidan sin problemas. En este ejemplo, nos gustaría que las cuatro funciones siguientes, conocidas como mapas de transición, fueran continuas:

• \(\phi_{L}\)en función de\(\phi_{R}\) en el dominio\(0 < \phi_{R} < \pi\)
• \(\phi_{L}\)en función de\(\phi_{R}\) en el dominio\(− \pi < \phi_{R} < 0\)
• \(\phi_{R}\)en función de\(\phi_{L}\) en el dominio\(0 < \phi_{L} < \pi\)
• \(\phi_{R}\)en función de\(\phi_{L}\) L en el dominio\(\pi < \phi_{L} < 2 \pi\)

La definición de coordenadas locales solo establece que un colector puede ser coordinado. Es decir, las funciones que definen los mapas de coordenadas no forman parte de la definición del colector, por lo que, por ejemplo, si dos personas definen parches de coordenadas en el círculo unitario de diferentes maneras, siguen hablando exactamente del mismo colector.

Ejemplo 21: Segmento lineal abierto homeomórfico a una línea

Deje que L sea un segmento de línea abierto, como el intervalo abierto (0, 1). L es homeomórfico a una línea, porque podemos mapear (0, 1) a la línea real a través de la función f (x) = tan (\(\pi x − \frac{\pi}{2}\)).

Ejemplo 22: Segmento de línea cerrada no homeomórfico a una línea

Un segmento de línea cerrada (que no es un colector) no es homeomórfico a una línea. Si lo mapeamos a una línea, entonces los puntos finales tienen que ir a dos puntos especiales A y B. Entonces no hay manera de que el mapeo visite los puntos exteriores al intervalo [A, B] sin visitar A y B más de una vez.

Ejemplo 23: Segmento lineal abierto no homeomórfico al interior de un círculo

Si el interior de un círculo pudiera ser mapeado por un homeomorfismo f a un segmento lineal abierto, entonces consideremos qué pasaría si tomáramos una curva cerrada que se encuentra dentro del círculo y encontramos su imagen. Por el teorema del valor intermedio, f no sería uno a uno, pero esto es una contradicción ya que se asumió que f era un homeomorfismo. Este es un ejemplo de un hecho más general de que el homeomorfismo preserva la dimensionalidad de un múltiple.

Figura\(\PageIndex{5}\)

Colectores Diferenciables

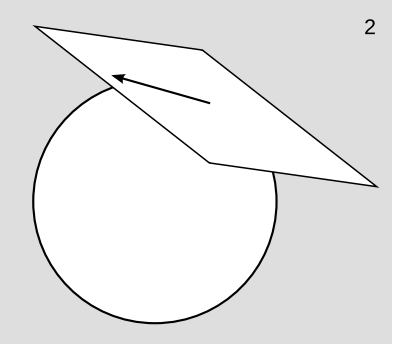
Un colector diferenciable significa un colector con suficiente estructura adicional para que pueda hacer cálculos en él, pero esta estructura adicional no necesariamente incluye nada tan elegante como una métrica. Como ejemplo concreto, supongamos que en un universo galileo 1 + 1-dimensional, la observadora Alice construye un sistema de coordenadas global (t, x). Su espacio-tiempo es claramente un múltiple, basado en la definición de coordenadas locales, y esto es cierto a pesar de que el espacio-tiempo galileo no tiene una métrica. En tanto, el observador Bob construye su propio sistema de coordenadas (t', x'). Pero algo perturbador sucede cuando Alice construye el mapa de transición de la cuadrícula de coordenadas de Bob a la suya. Como se muestra en la figura f, la cuadrícula de Bob tiene una torceduras en ella. “Bob”, dice Alice, “algo anda mal con tu sistema de coordenadas. Hago la hipótesis de que en cierto momento, al que podemos llamar t = 0, un gigante invisible golpeó tu cuerpo con un mazo de croquet invisible y de repente cambió tu estado de movimiento”. “De ninguna manera, Alice”, responde Bob. “No sentí que pasara nada a t = 0. Creo que tú eres a quien le dieron una paliza”.

Figura\(\PageIndex{6}\) - “¡Bob, tu colector no es suave!”

Por un colector diferenciable nos referimos a uno en el que este tipo de controversia nunca ocurre. El colector viene con una colección de sistemas de coordenadas locales, llamados gráficos, y dondequiera que estos gráficos se superpongan, el mapa de transición es diferenciable. Cada coordenada es una función diferenciable de cualquier otra coordenada. De hecho, asumiremos por conveniencia que no sólo se define la primera derivada sino derivados de todos los órdenes. Esto hace que nuestro colector no solo sea un colector diferenciable sino un colector liso. Esta definición suena dependiente de coordenadas, pero no lo es. Nuestra colección de gráficos (llamada atlas) puede contener infinitamente muchos sistemas de coordenadas posibles; incluso podemos especificar que contiene todos los sistemas de coordenadas posibles que podrían obtenerse unos de otros por cualquier diffeomorfismo.

El espacio tangente

Ahora formalizamos la noción intuitiva de un vector tangente (sección 3.1), siguiendo a Nowik y Katz. ¹⁹ Que M sea un colector liso n-dimensional, de modo que localmente se vea como el espacio euclidiano, descriptible por las coordenadas de número real x, y,. .Ahora mejoramos M para formar un nuevo espacio topológico, en el que las coordenadas pueden incluir no solo números reales, sino números que difieren infinitesimalmente de reales, como se indica en el ejemplo 3. A partir de ahora cuando decimos cosas como “el colector”, nos referimos a esta versión mejorada. ²⁰ Fijar algún número infinitesimal de una vez\(\epsilon\) por todas, y definir la notación x = O (\(\epsilon\)) para significar que no\(\frac{x}{\epsilon}\) es infinito. ²¹

Nota

Es posible definir una mejora diferente y mayor, llamada ^∗ M, que incluiría puntos con coordenadas infinitamente grandes. Por ejemplo, supongamos que tenemos un parche de coordenadas con límites en las coordenadas que se pueden anotar usando desigualdades, t > 0, 0\(\theta\) ≤ ≤\(\frac{\pi}{4}\),. Entonces ^∗ M contendría cualquier valor finito, infinitesimal e infinito de (t,\(\theta\),..) satisfaciendo estas desigualdades, y esto incluiría valores infinitos de t. No lo haremos aquí, porque la inclusión de puntos idealizados en el infinito es más útil en la relatividad si lo hacemos usando un enfoque diferente, discutido en la sección 7.3.

Nota

Una definición equivalente y manifiestamente independiente de la coordinación es que por cada función real suave en una vecindad de los puntos, la función difiere en estos puntos por una cantidad que es O (\(\epsilon\)).

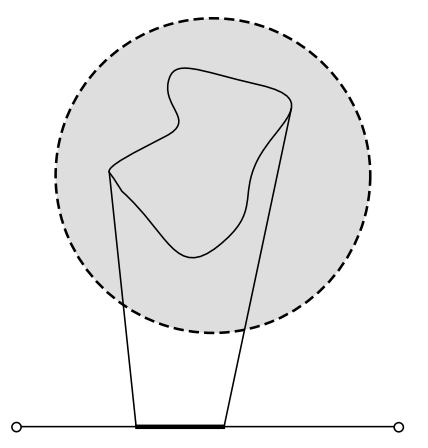
Los puntos en el colector se consideran cercanos si la distancia euclidiana entre ellos en el espacio de coordenadas es O (\(\epsilon\)). Esta definición suena dependiente de coordenadas, pero no lo es, y suena como si estuviera asumiendo una métrica euclidiana real, pero no lo es. ²² Define un prevector en el punto P como un par (P, Q) de puntos que están cerca, Figura 5.10.7 (1). Definir a los prevalecientes para que sean equivalentes si la diferencia entre ellos es infinitesimal incluso comparada con\(\epsilon\).

Figura\(\PageIndex{7}\) - 1. Un vector tangente puede considerarse como un desplazamiento infinitesimal. 2. Para una esfera incrustada en tres espacios, el espacio de vectores tangentes se visualiza como un plano tangente a la esfera en cierto punto.

Definición

Un vector tangente en el punto P es el conjunto de todos los precursores en P que son equivalentes a un prevector particular en P.

El espacio tangente T _P es el conjunto de todos los vectores tangentes en P. El espacio tangente tiene la estructura de un espacio vectorial sobre los reales simplemente usando las diferencias de coordenadas para definir las operaciones vector-espacio, tal como haríamos si (P, Q) significara una flecha que se extiende de P a Q, como en física de primer año.

En la práctica, realmente no nos importan los detalles de la construcción del espacio tangente, y diferentes personas ni siquiera tienen que usar la misma construcción. Todo lo que nos importa es que el espacio tangente tenga cierta estructura. En particular, tiene n dimensiones, como esperaríamos intuitivamente. Ya que vamos a olvidar los detalles de la construcción, no importa que hayamos hecho infinitesimales por definición todos los vectores tangentes. La estructura interna del espacio vectorial solo tiene que ver con cuán grandes son los vectores comparados entre sí. (Si quisiéramos, podríamos escalar todos los vectores tangentes por un factor de\(\frac{1}{\epsilon}\).) Esto justifica la visualización en la Figura 5.10.7 (2).

En realidad no es del todo cierto que solo nos importa la estructura interna del espacio tangente, porque entonces podríamos haber evitado la definición elegante y simplemente usar el espacio vectorial ordinario que consiste en n-tuplas de números reales. La definición de fantasía es necesaria porque vincula el espacio tangente de manera natural a la estructura del colector en un punto particular. Por lo tanto, nos permitirá (1) definir el transporte paralelo, que lleva un vector de un espacio tangente a otro, y (2) definir componentes de vectores en un sistema de coordenadas particular.

Para una definición alternativa del espacio tangente, véase el capítulo 2 de Carroll. ²³ Brevemente, esto implica tomar un vector tangente para que sea algo que se comporte como una derivada direccional. En particular, una derivada parcial con respecto a una coordenada tal como\(\frac{\partial}{\partial x}\) califica como un vector tangente, que pensamos que apunta en la dirección x. El conjunto de tales derivadas de coordenadas forma una base para el espacio tangente y proporciona una manera conveniente de anotar vectores tangentes. Encontraremos esta notación conveniente en la sección 7.1.

Referencias

¹⁹ “Geometría diferencial mediante desplazamientos infinitesimales”, arxiv.org/abs/1405.0984

²³ Ponencia Apuntes sobre Relatividad General, http://ned.ipac.caltech.edu/level5/March01/Carroll3/Carroll_contents.html.