5.11: Colector (Parte 1)

Esta sección se puede omitir en una primera lectura.

Por qué necesitamos colectores

La relatividad general no asume una métrica de fondo predefinida, y esto crea un problema de pollo y huevo. Queremos definir una métrica en algún espacio, pero ¿cómo especificamos siquiera el conjunto de puntos que conforman ese espacio? La forma habitual de definir un conjunto de puntos sería por sus coordenadas. Por ejemplo, en dos dimensiones podríamos definir el espacio como el conjunto de todos los pares ordenados de números reales (x, y). Pero esto no funciona en la relatividad general, porque no se garantiza que el espacio tenga esta estructura. Por ejemplo, en el clásico juego de computadora Asteroides de 1979, el espacio “se envuelve”, de modo que si tu nave espacial vuela por el borde derecho de la pantalla, reaparece a la izquierda, y de manera similar en la parte superior e inferior (Figura\(\PageIndex{1}\)).

Figura\(\PageIndex{1}\): En Asteroides, el espacio “envuelve”.

Incluso antes de imponer una métrica a este espacio, tiene propiedades topológicas que difieren de las del plano euclidiano. Por “topológico” nos referimos a propiedades que se conservan si se piensa en el espacio como una lámina de goma que se puede estirar de cualquier manera, pero no cortar ni volver a pegarse. Topologicamente, el espacio en Asteroides es equivalente a un toro (superficie de una rosquilla), pero no al plano euclidiano.

Figura\(\PageIndex{2}\): Una taza de café es topológicamente equivalente a un toro.

Otro ejemplo útil es la superficie de una esfera. En el ejemplo 10, calculamos\(\Gamma^{\theta}_{\phi \phi}\). Un cálculo similar da\(\Gamma^{\theta}_{\phi \phi} = \cot \frac{\theta}{R}\). Ahora considere lo que sucede cuando conducimos nuestro trineo de perros hacia el norte por la línea de longitud\(\phi\) = 0, cruzamos el polo norte en\(\theta\) = 0, y continuamos por la misma geodésica. Al cruzar el polo, nuestra longitud cambia discontinuamente de 0 a\(\pi\). Consultando la ecuación geodésica, vemos que esto sucede porque\(\Gamma^{\theta}_{\phi \phi}\) explota en\(\theta\) = 0. Por supuesto que nada realmente especial pasa en el polo. El mal comportamiento no es culpa de la esfera, es culpa de las\((\theta, \phi)\) coordenadas que hemos elegido, que pasan a portarse mal en el polo. Desafortunadamente, es imposible definir un par de coordenadas en una dos esferas sin que se porten mal en alguna parte. (Esto se desprende del famoso “Teorema de pelota peluda” de 1912 de Brouwer, que afirma que es imposible peinar el cabello en una esfera sin crear un cowlick en alguna parte.)

Definición topológica de un colector

Esto nos motiva a tratar de definir un espacio geométrico “básico” en el que no existe una métrica predefinida o incluso un conjunto predefinido de coordenadas.

Existe una noción general de espacio topológico, que es demasiado general para nuestros fines. En tal espacio, la única estructura que se nos garantiza es que ciertos conjuntos se definen como “abiertos”, en el mismo sentido que un intervalo como 0 < x < 1 se llama “abierto”. Un punto en un conjunto abierto se puede mover en cualquier dirección sin salir del conjunto. Un conjunto abierto es esencialmente un conjunto sin límite, ya que en un conjunto como 0 ≤ x ≤ 1, los puntos de límite 0 y 1 solo se pueden mover en una dirección sin sacarlos afuera.

Figura\(\PageIndex{3}\): La relatividad general no asume una métrica de fondo predefinida. Por lo tanto, todo lo que realmente podemos saber antes de calcular nada es que estamos trabajando en un colector, sin que se le imponga una métrica.

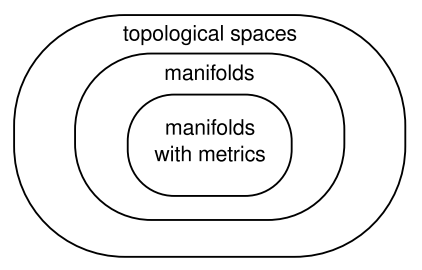
Un espacio topológico es demasiado general para nosotros porque puede incluir espacios como fractales, espacios infinito-dimensionales y espacios que tienen diferentes números de dimensiones en diferentes regiones. Sin embargo, es útil reconocer ciertos conceptos que pueden definirse utilizando únicamente el aparato genérico de un espacio topológico, para que sepamos que no dependen en modo alguno de la presencia de una métrica. Un conjunto abierto que rodea un punto se llama barrio de ese punto. En un espacio topológico tenemos la noción de acercarnos arbitrariamente a cierto punto, lo que significa tomar barrios cada vez más pequeños, cada uno de los cuales es un subconjunto de los últimos. Pero como no hay métrica, no tenemos ningún concepto de comparar distancias de puntos distantes, por ejemplo, que P está más cerca de Q que R es de S. Una función continua es una idea puramente topológica; una función continua es aquella tal que para cualquier subconjunto abierto U de su rango, el conjunto V de puntos en su dominio que son mapeado a puntos en U también está abierto. Aunque algunas definiciones de funciones continuas hablan de números reales como\(\epsilon\) y\(\delta\), la noción de continuidad no depende de la existencia de ninguna estructura como el sistema de números reales. Un homeomorfismo es una función que es invertible y continua en ambas direcciones. Los homeomorfismos formalizan la noción informal de “geometría de lámina de caucho sin cortar ni pegar”. Si existe un homeomorfismo entre dos espacios topológicos, decimos que son homeomórficos; tienen la misma estructura y son en cierto sentido el mismo espacio.

El tipo más específico de espacio topológico que queremos se llama colector. Sin intentar ningún alto nivel de rigor matemático, definimos un colector n-dimensional M de acuerdo con los siguientes principios informales: ¹⁶

Nota

Para aquellos con conocimiento de topología, estos se pueden formalizar un poco más: queremos un espacio topológico completamente normal, segundo contable, conectado localmente que tenga Lebesgue cubriendo la dimensión n, sea un espacio homogéneo bajo su propio grupo de homeomorfismo, y sea un espacio completo uniforme. No sé si esto es suficiente para caracterizar completamente a un colector, pero basta con descartar todos los contraejemplos de los que conozco.

• Dimensión M1: La dimensión de M es n.
• M2 Homogeneidad: Ningún punto tiene ninguna propiedad localmente definible que lo distinga de cualquier otro punto.
• M3 Completitud: M es completa, en el sentido de que especificar un vecindario arbitrariamente pequeño da una definición única de un punto.

Ejemplo 12: Líneas

El conjunto de todos los números reales es un 1-manifold. Del mismo modo, cualquier línea con las propiedades especificadas en Elementos de Euclides es un colector 1. Todas esas líneas son homeomórficas entre sí, y por lo tanto podemos hablar de “la línea”.

Ejemplo 13: un círculo

Un círculo (sin incluir su interior) es un 1-colector, y no es homeomórfico a la línea. Para ver esto, tenga en cuenta que eliminar un punto de un círculo lo deja en una pieza conectada, pero eliminar un punto de una línea hace dos. Aquí utilizamos el hecho de que un homeomorfismo está garantizado para preservar propiedades de “lámina de goma” como el número de piezas.

Ejemplo 14: Sin cambios de dimensión

Una “piruleta” formada al pegar un círculo 2 abierto (es decir, un círculo que no incluye su límite) a un segmento de línea abierta no es un colector, porque no hay n para el que satisfaga M1.

También viola M2, porque los puntos de este conjunto caen en tres clases distintas: clases que viven en barrios bidimensionales, las que viven en barrios unidimensionales, y el punto donde el segmento lineal cruza el límite del círculo.

Ejemplo 15: No hay colectores hechos a partir de los números racionales

Los números racionales no son múltiples, porque especificar un vecindario arbitrariamente pequeño alrededor\(\sqrt{2}\) excluye cada número racional, violando a M3.

De manera similar, el plano racional definido por pares de coordenadas de número racional (x, y) no es un colector de 2. Es bueno que hayamos excluido este espacio, porque tiene la propiedad antifísica de que las curvas pueden cruzar sin tener un punto en común. Por ejemplo, la curva y = x ² cruza de un lado de la línea y = 2 al otro, pero nunca la cruza. Esto es físicamente indeseable porque no concuerda con lo que tenemos en mente cuando hablamos de colisiones entre partículas como intersecciones de sus líneas mundiales, o cuando decimos que las líneas de campo eléctrico no se supone que se crucen.

Ejemplo 16: sin límite

El semiplano abierto y > 0 en el plano cartesiano es un colector de 2. El semiplano cerrado y ≥ 0 no lo es, porque viola M2; los puntos límite tienen propiedades diferentes a las del interior.

Ejemplo 17: Colector desconectado

Dos líneas que no se intersectan son un colector de 1. Físicamente, colectores desconectados de este tipo representarían un universo en el que un observador de una región nunca podría conocer la existencia de la otra región.

Ejemplo 18: No hay malos trabajos de pegamento

Toma tus manos como si estuvieras fingiendo que conoces el karate, y luego usa una mano para cortar karate a la otra. Supongamos que queremos unir dos medios planos abiertos de esta manera. Mientras estén separados, entonces tenemos un colector desconectado perfectamente legítimo. Pero si queremos unirnos a ellos sumando el punto P donde coinciden sus límites, entonces violamos M2, porque este punto tiene propiedades especiales no poseídas por ningún otro. Un ejemplo de tal propiedad es que existen puntos Q y R de tal manera que cada curva continua que los une pasa por P. (Cf. problema 5)

Hausdorff Propiedad

El topólogo pionero Felix Hausdorff definió la siguiente propiedad de un espacio topológico.

Definición: Propiedad de Hausdorff

Dados dos puntos cualesquiera, es posible encontrar barrios disjuntos de ellos.

Una broma o mnemotécnico, que probablemente funciona mejor para personas con cierto tipo de acento británico, es que en un espacio de Hausdorff, dos puntos cualesquiera pueden ser “alojados” uno del otro dentro de sus propios sets abiertos que no se intersectan. La noción apela fuertemente a nuestras ideas intuitivas sobre cómo se comportan el espacio y el tiempo, y la definición estándar de un múltiple implica que es Hausdorff. Cuando modelamos el espacio Minkowski usando coordenadas de número real, es Hausdorff. Dado que el principio de equivalencia dice que el espacio-tiempo es localmente Minkowski, también podríamos decir que implica que el espacio-tiempo es Hausdorff. No obstante, la relatividad general permite que el espacio-tiempo se comporte mal en casos como las singularidades, por lo que es imaginable que nuestro universo contenga puntos que violen la propiedad de Hausdorff. Hay espaciotiempos interesantes y físicamente bien motivados, como algunas versiones del espacio Taub-nut, que no son Hausdorff. Como no tenemos datos empíricos sobre el comportamiento del espacio-tiempo bajo las condiciones más extremas, no podemos decir si el espacio-tiempo es realmente Hausdorff. Se debe mantener cierto escepticismo sobre si tal categoría idealizada es incluso significativa en la ciencia, ya que se refiere a fenómenos a escalas arbitrariamente pequeñas, mientras que las teorías y mediciones están limitadas en las escalas que pueden tratar. Earman da una buena discusión sobre la propiedad de Hausdorff aplicada a la relatividad. ¹⁷

Ejemplo 19: Universos ramificados

La figura\(\PageIndex{4}\) muestra diagramas espacio-tiempo de universos 1 + unidimensionales que se ramifican como un árbol. Estas pretenden ser imágenes de la relatividad general clásica, aunque parte de la motivación más fuerte para considerar tales posibilidades proviene de los intentos de construir una teoría de la gravedad cuántica. En tales teorías, comúnmente se espera que el espacio-tiempo tenga una estructura a la escala de Planck que sea una especie de “espuma cuántica”.

Figura\(\PageIndex{4}\): S diagramas pacetime de universos 1 + unidimensionales.

El ejemplo en la Figura\(\PageIndex{4A}\) es un colector, y es Hausdorff. Este es un ejemplo de cambio de topología, lo que significa que la sección espacial en un momento tiene una topología diferente a la sección en otro. ¹⁸ Aunque tal ramificación puede ocurrir sin la existencia de singularidades, los teoremas de Tipler y Geroch muestran que deben ocurrir otros tipos de mala conducta, incluyendo violaciones de causalidad y la necesidad de formas de materia que violen las condiciones energéticas.

La figura\(\PageIndex{4B}\) es cualitativamente diferente. Aquí hemos formado un espacio-tiempo pegando tres piezas. No hay curvatura implícita; estas podrían ser tres piezas del espacio Minkowski. El espacio-tiempo no es múltiple, ya que los puntos en la unión tienen diferentes propiedades locales que los puntos en otros lugares. La maquinaria de la relatividad general se descompone en un caso como este, pero por ejemplo podríamos imaginar que una geodésica en este espacio-tiempo podría bifurcarse en dos geodésicas distintas tras la división.

Sin embargo, una tercera posibilidad es reinterpretar Figura\(\PageIndex{4B}\) para que haya dos copias diferentes de la costura. Por ejemplo, podríamos dejar que la porción del diagrama que se extiende hacia el pasado sea representada por puntos con t < 0, mientras que las dos ramas que continúan hacia el futuro podrían tener cada una t ≥ 0, de modo que para una x dada tendríamos dos eventos diferentes con coordenadas (t = 0, x). No sería posible poner estos dos puntos en barrios disjuntos, por lo que esta versión del espacio no es Hausdorff.

---

¹⁸ Para un tratamiento reciente, véase Borde, 1994, “Cambio topológico en la relatividad general clásica”, arxiv.org/abs/gr-qc/9406053.

Referencias

¹⁷ John Earman, 'Podar algunas ramas de “ramificación de espaciotiempos”, 'Pitt.edu/~Jearman/earman2008a.pdf