5.10: De Métrico a Curvatura

Encontrar el símbolo de Christoffel a partir de la métrica

Ya encontramos el símbolo de Christoffel en términos de la métrica en una dimensión. Expresándolo en notación tensora, tenemos

\[\Gamma^{d}_{ba} = \frac{1}{2} g^{cd} (\partial_{?} g_{??}),\]

donde la inversión de la matriz de un componente G ha sido reemplazada por inversión matricial y, lo que es más importante, los signos de interrogación indican que habría más de una manera de colocar los subíndices de manera que el resultado fuera una ecuación de tensor gramatical. La forma más general para el símbolo de Christoffel sería

\[\Gamma^{b}_{ac} = \frac{1}{2} g^{db} (L \partial_{c} g_{ab} + M \partial_{a} g_{cb} + N \partial_{b} g_{ca}),\]

donde\(L\),\(M\), y\(N\) son constantes. La consistencia con la expresión onedimensional requiere

\[L + M + N = 1\]

y la torsión que se desvanece da\(L = M\). Los\(M\) términos\(L\) y tienen un significado físico diferente al\(N\) término.

Supongamos que un observador usa coordenadas tales que todos los objetos se describen como alargados con el tiempo, y el cambio de escala acumulado a lo largo de un día es un factor de k > 1. Esto es descrito por la derivada\(\partial_{t} g_{xx}\) < 1, que afecta al\(M\) término. Dado que la métrica se utiliza para calcular distancias cuadradas, el elemento de la matriz g _xx se escala hacia abajo por\(\frac{1}{\sqrt{k}}\). Para compensar\(\partial_{t} v^{x} < 0\), entonces necesitamos agregar un término de corrección positiva,\(M > 0\), a la derivada covariante. Cuando el mismo observador mide la tasa de cambio de un vector\(v^t\) con respecto al espacio, la tasa de cambio resulta ser demasiado pequeña, porque la variable que diferencia con respecto a la que se diferencia es demasiado grande. Esto requiere\(N < 0\), y la corrección es del mismo tamaño que la\(M\) corrección th, entonces\(|M| = |N|\). Nos encontramos\(L = M = −N = 1\).

Ejercicio\(\PageIndex{1}\)

¿El argumento anterior depende del uso del espacio para una coordenada y el tiempo para la otra?

La expresión general resultante para el símbolo de Christoffel en términos de la métrica es

\[\Gamma^{c}_{ab} = \frac{1}{2} g^{cd} (\partial_{a} g_{bd} + \partial_{b} g_{ad} - \partial_{d} g_{ab}) \ldotp\]

Uno puede volver fácilmente y comprobar que esto da

\[\nabla_{c} g_{ab} = 0. \label{eq10}\]

Confirmar la ecuación\ ref {eq10} es un poco tedioso. Para el caso, los cálculos de tensores en general pueden consumir mucho tiempo y ser propensos a errores. Cualquier persona razonable que viva en el siglo XXI, por lo tanto, recurrirá a un sistema de álgebra informática. El sistema de álgebra computacional más utilizado es Mathematica, pero es caro y patentado, y no tiene amplias instalaciones incorporadas para manejar tensores. Resulta que hay bastante software tensor gratuito y de código abierto, y se divide en dos clases: basado en coordenadas e independiente de coordenadas. La mejor instalación de código abierto independiente de coordinación disponible parece ser Cadabra, y de hecho la verificación de\(\nabla_{c} g_{ab}\) = 0 es el primer ejemplo dado en la práctica guía de Leo Brewin sobre aplicaciones de Cadabra a la relatividad general. ¹³

Ejercicio\(\PageIndex{2}\)

En el caso de 1 dimensión, mostrar que esto se reduce al resultado anterior de\(−(\frac{1}{2}) \frac{dG}{dX}\).

Al\(\Gamma\) no ser un tensor, no es obvio que el derivado covariante, que se construye a partir de él, sea un tensor. Pero si no es obvio, tampoco es sorprendente —el objetivo de la derivación anterior era obtener resultados que fueran independientes de la coordinación.

Ejemplo 10: Símbolos de Christoffel en el globo, cuantitativamente

En el ejemplo 9, inferimos las siguientes propiedades para el símbolo de Christoffel\(\Gamma^{\theta}_{\phi \phi}\) en una esfera de radio R:\(\Gamma^{\theta}_{\phi \phi}\) es independiente de\(\phi\) y R,\(\Gamma^{\theta}_{\phi \phi}\) < 0 en el hemisferio norte (colatitud θ menor que π/2),\(\Gamma^{\theta}_{\phi \phi}\) = 0 en el ecuador, y\(\Gamma^{\theta}_{\phi \phi}\) > 0 en el hemisferio sur.

La métrica en una esfera es

\[ds^2 = R^2 d\theta^{2} + R^2 \sin^2 \theta d\phi^{2}.\]

El único término que no se desvanece en la expresión for\(\Gamma^{\theta}_{\phi \phi}\) es el que involucra\(\partial_{\theta} g_{\phi \phi} = 2R^{2} \sin \theta \cos \theta\). El resultado es

\[\Gamma^{\theta}_{\phi \phi} = − \sin \theta \cos \theta\]

que se puede verificar para tener las propiedades reclamadas anteriormente.

Solución Numérica de la Ecuación Geodésica

En la Sección 5.7, di un algoritmo que demostró la singularidad de las soluciones a la ecuación geodésica. Este algoritmo también se puede utilizar para encontrar geodésicas en los casos en que se conozca la métrica. El siguiente programa, escrito en el lenguaje informático Python, realiza un cálculo muy sencillo de este tipo, en un caso en el que sabemos cuál debe ser la respuesta; incluso sin ninguna familiaridad previa con Python, no debería ser difícil ver la correspondencia entre el algoritmo abstracto presentado en Sección 5.7 y su realización concreta a continuación. Para coordenadas polares en un plano euclidiano, se puede calcular\(\Gamma^{r}_{\phi \phi}\) = −r y\(\Gamma^{\phi}_{r \phi} = \frac{1}{r}\) (problema 2). Aquí calculamos la geodésica que comienza tangente al círculo unitario en\(\phi=0\).

No es necesario preocuparse por todos los detalles técnicos del idioma (por ejemplo, la línea 1, que pone a disposición comodidades como math.pi para\(\pi\)). Los comentarios se ponen en marcha por signos de libra. Las líneas 16-34 están sangradas porque todas deben ser ejecutadas repetidamente, hasta que ya no sea cierto eso\(\lambda < \lambda_{max}\) (línea 15).

Ejercicio\(\PageIndex{3}\)

Al inspeccionar las líneas 18-22, encontrar las señales de\(\ddot{r}\) y\(\ddot{\phi}\) en\(\lambda\) = 0. Convénzase de que estos signos son lo que esperamos geométricamente.

La salida es la siguiente:

Podemos ver eso\(\phi\) → 90 deg. as\(\lambda \rightarrow \infty\), lo cual tiene sentido, porque lo geodésico es una línea recta paralela al eje y. Un uso menos trivial de la técnica se demuestra en la Sección 6.2, donde se calcula la desviación de los rayos de luz en un campo gravitacional, una de las pruebas observacionales clásicas de relatividad general.

El tensor Riemann en términos de los símbolos de Christoffel

La derivada covariante de un vector puede interpretarse como la velocidad de cambio de un vector en una dirección determinada, en relación con el resultado de transportar en paralelo el vector original en la misma dirección. Por lo tanto, podemos ver que la definición del tensor de curvatura de Riemann en la Sección 5.4 es una medida de la falla de las derivadas covariantes para conmutar:

\[(\nabla_{a} \nabla_{b} - \nabla_{b} \nabla_{a}) A^{c} = A^{d} R^{c}_{dab}\]

Un tedioso cálculo da ahora\(R\) en términos de la\(\Gamma\) s:

\[R^{a}_{bcd} = \partial_{c} \Gamma^{a}_{db} - \partial_{d} \Gamma^{a}_{cb} + \Gamma^{a}_{ce} \Gamma^{e}_{db} - \Gamma^{a}_{de} \Gamma^{e}_{cb}\]

Esto se da como otro ejemplo más adelante en el manual de Brewin para aplicar Cadabra a la relatividad general. ¹⁴ (Brewin escribe el índice superior en la segunda ranura de R.)

Algunas ideas generales sobre Gauge

Retrocedamos ahora por un momento y tratemos de obtener un poco de conocimiento físico al observar las características que tienen en común las transformaciones de calibre electromagnético y relativista. Tenemos las siguientes analogías:

	electromagnetismo	geometría diferencial
simetría global	Un desplazamiento de fase constante no\(\alpha\) tiene efectos observables.	Agregar una constante a una coordenada no tiene efectos observables.
simetría local	Un cambio de fase\(\alpha\) que varía de un punto a otro no tiene efectos observables.	Una transformación arbitraria de coordenadas no tiene efectos observables.
El calibre es descrito por.	\(\alpha\)	\(g_{\mu \nu}\)
.. y la diferenciación de esto da el campo de calibre..	A b	\(\Gamma^{c}_{ab}\)
Una segunda diferenciación da el (los) campo (s) directamente observable (s).	E y B	\(R^c_{dab}\)

Lo interesante aquí es que los campos directamente observables no llevan toda la información necesaria, pero los campos de calibre no son directamente observables. En el electromagnetismo, podemos ver esto a partir del efecto Aharonov-Bohm, mostrado en la Figura\(\PageIndex{1}\). ¹⁵ El solenoide tiene B = 0 externamente, y los haces de electrones solo se mueven alguna vez a través de la región externa, por lo que nunca experimentan ningún campo magnético. Los experimentos muestran, sin embargo, que encender y apagar el solenoide sí cambia la interferencia entre los dos haces. Esto se debe a que el potencial vectorial no se desvanece fuera del solenoide, y como hemos visto en la sección 4.2, la fase de los haces varía según la integral de trayectoria del A _b. Por lo tanto, nos quedamos con una situación incómoda, pero inevitable. Se supone que el concepto de campo elimina la necesidad de acción instantánea a distancia, lo cual está prohibido por la relatividad; es decir, (1) queremos que nuestros campos tengan sólo efectos locales. Por otro lado, (2) nos gustaría que nuestros campos fueran cantidades directamente observables. No podemos tener tanto 1 como 2. El campo de calibre satisface 1 pero no 2, y los campos electromagnéticos dan 2 pero no 1.

Figura\(\PageIndex{1}\): El efecto Aharonov-Bohm. Un electrón entra en un divisor de haz en P, y se envía en dos direcciones diferentes. Las dos partes de la onda se reflejan de manera que se reúnen en Q. Las flechas representan el potencial vectorial A. El campo magnético observable B es cero en todas partes fuera del solenoide, y sin embargo la interferencia observada en Q depende de si el campo está encendido. Consulte la sección 4.2 para una mayor discusión de los campos A y B de un solenoide.

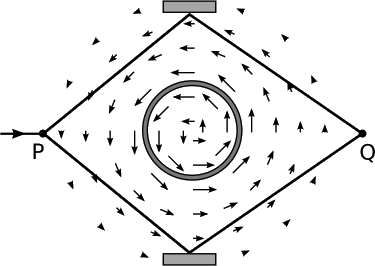
Nota

Aquí se describe el efecto en términos de un experimento idealizado y poco práctico. Para conocer el estado empírico real del efecto Aharonov-Bohm, véase Batelaan y Tonomura, Physics Today 62 (2009) 38.

La Figura 5.9.2 muestra un análogo del experimento Aharonov-Bohm en geometría diferencial. En todas partes menos en la punta, el cono tiene curvatura cero, como podemos ver cortándolo y colocándolo plano. Pero incluso un observador que nunca visita la región fuertemente curvada en la punta puede detectar su existencia, porque el transporte paralelo de un vector alrededor de un bucle cerrado puede cambiar la dirección del vector, siempre que el bucle rodee la punta.

Figura\(\PageIndex{2}\) - El cono tiene curvatura intrínseca cero en todas partes excepto en su punta. Un observador que nunca visita la punta puede, sin embargo, detectar su existencia, porque el transporte paralelo alrededor de un camino que encierra la punta provoca que un vector cambie su dirección.

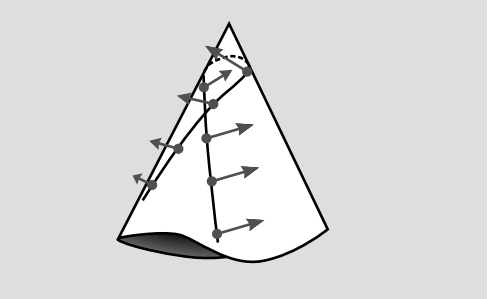
En el ejemplo electromagnético, la integración de A alrededor de un bucle cerrado revela, a través del teorema de Stokes, la existencia de un flujo magnético a través del bucle, a pesar de que el campo magnético es cero en cada ubicación donde A tiene que ser muestreado. En el ejemplo relativista, la integración\(\Gamma\) alrededor de un bucle cerrado muestra que hay curvatura dentro del bucle, aunque la curvatura es cero en todos los lugares donde se\(\Gamma\) tiene que muestrear.

El hecho de que\(\Gamma\) sea un campo medidor, y por lo tanto no observable localmente, es simplemente una manera elegante de expresar las ideas introducidas en la sección 5.6, que debido al principio de equivalencia, el campo gravitacional en la relatividad general no es localmente observable. Esta no observabilidad es local porque el principio de equivalencia es una declaración sobre los marcos locales de Lorentz. El ejemplo en la Figura 5.9.2 es no local.

Ejemplo 11: Efecto geodésico y estructura de la fuente

• En la Sección 5.5, se estimó el efecto geodésico sobre la sonda de gravedad B y se encontró un resultado que solo se apagó por un factor de 3\(\pi\). La forma matemáticamente pura del 3\(\pi\) sugiere que el efecto geodésico es insensible a la distribución de la masa dentro de la tierra. ¿Por qué debería ser así?
• El cambio en un vector al transportarlo en paralelo alrededor de un bucle cerrado se puede expresar en términos de (1) el área integral de la curvatura dentro del bucle o (2) la integral de línea del símbolo de Christoffel (esencialmente el campo gravitacional) en el bucle mismo. A pesar de que expresé la estimación como 1, habría sido igualmente válido usar 2. Según el teorema de la concha de Newton, el campo gravitacional no es sensible a nada sobre su distribución de masa que no sea su simetría casi esférica. La tierra gira, y esto sí afecta al tensor de tensión-energía, pero dado que la velocidad con la que gira es en todas partes mucho menor que c, el efecto resultante, llamado arrastre de fotogramas, es mucho menor.

Referencias

¹³ http://arxiv.org/abs/0903.2085

¹⁴ http://arxiv.org/abs/0903.2085