8.7: Soluciones Cosmológicas (Parte 4)

La solución dominada por la radiación

Por las razones discutidas en el ejemplo 14, el universo primitivo estuvo dominado por la radiación. La solución de las ecuaciones de Friedmann para este caso se retoma en el problema 11.

Efectos locales de la expansión

En esta sección discutimos las predicciones de la relatividad general sobre el efecto de la expansión cosmológica en sistemas pequeños, gravitacionalmente ligados como el sistema solar o cúmulos de galaxias. La respuesta corta es que en las cosmologías más realistas (pero no necesariamente en escenarios de “Big Rip”) el efecto de expansión no es cero, sino que es muchos órdenes de magnitud demasiado pequeño para medirlo. Muchos lectores probablemente estarán dispuestos a aceptar estas afirmaciones mientras se saltan las siguientes demostraciones.

Para empezar, observamos que existen dos tipos de efectos cualitativamente distintos que podrían existir. Supongamos que una hogaza de pan de pasas está levantando. Digamos que el factor de escala del pan a se duplica en el momento en que se gastan los esfuerzos de la levadura. Por definición, esto significa que las pasas (galaxias, partículas de prueba) se separan más en un factor de 2. Podríamos imaginar que además: (1) la tensión de expansión podría hacer que cada pasa se inflara en, digamos, 1%, y mantener este aumento de tamaño a lo largo de todo el curso de la expansión; o que (2) la expansión podría hacer que cada pasa se expanda gradualmente, a 0.2% más que su tamaño original, luego 0.4% más que su tamaño original, y así sucesivamente, hasta que, al final del proceso, cada uno había crecido más allá de su tamaño original en alguna cantidad como 3.8%, que, si bien menos del crecimiento del 100% de las distancias entre pasas, era sin embargo distinto de cero. Los astrónomos se refieren a la segunda posibilidad como una tendencia “secular”. Por ejemplo, las simulaciones de sistemas solares a menudo muestran que a lo largo de miles de millones de años, los planetas migran gradualmente ya sea hacia adentro o hacia afuera, bajo la influencia de sus interacciones gravitacionales con otros planetas. Como ejemplo de una expansión sin una tendencia secular, los asteroides pueden experimentar una\(\frac{1}{r^{2}}\) fuerza no despreciable debido a la presión de radiación del sol. El efecto es exactamente como si la masa del sol o la constante gravitacional se hubieran reducido ligeramente. La ley de órbita elíptica de Kepler se mantiene, la ley de los períodos está ligeramente apagada y el radio orbital muestra una tendencia cero a lo largo del tiempo.

Si existe algún tipo de efecto, un observador en algún marco inercial local lo interpretará como una “fuerza”. (Las citas de miedo son un recordatorio de que la relatividad general no describe la gravedad como acción instantánea linealmente aditiva al estilo Newton a distancia). Tal fuerza, si existe, no puede ser simplemente proporcional a la tasa de expansión\(\frac{\dot{a}}{a}\). Como contraejemplo, el universo Milne es simplemente el espacio-tiempo plano descrito en coordenadas tontas, y lo ha hecho\(\dot{a} \neq 0\).

Tendría más sentido que la fuerza dependiera de la segunda derivada del factor escala. Para justificar esto con mayor precisión, imagina liberar dos partículas de prueba, inicialmente separadas por alguna distancia que es mucho menor que la escala del Hubble. Inicialmente están en reposo en relación con el flujo del Hubble, y no hay cuerpos gravitantes localmente presentes. Como se discutió en el ejemplo 15, la aceleración de una partícula de prueba con respecto a la otra viene dada por\((\frac{\ddot{a}}{a}\)) r, donde r es su desplazamiento relativo.

Por lo tanto, si vamos a observar algún efecto distinto de cero de la expansión en un sistema local, no son realmente efectos de expansión en absoluto, sino efectos de la aceleración de la expansión. El factor\(\frac{\ddot{a}}{a}\) está en el orden del cuadrado inverso de la edad del universo, es decir, H ² _o ∼ 10 ⁻³⁵ s ⁻². La pequeñez de este factor es lo que hace que el efecto sobre un sistema como el sistema solar sea tan absurdamente minúsculo.

Ejemplo 24: Un cuerpo humano

Estimemos el efecto de la expansión cosmológica sobre la longitud L de tu fémur. El cuerpo está hecho de átomos, y por las razones dadas anteriormente, no puede haber una tendencia constante en los tamaños de estos átomos o las longitudes de los enlaces químicos entre ellos. El hueso experimenta un estrés debido a la expansión cosmológica, pero está en equilibrio, y la deformación desaparecerá si se elimina la tensión gravitacional (por ejemplo, si se superponen otras tensiones gravitacionales sobre la cosmológica para cancelarla). La aceleración anómala entre los extremos del hueso es (\(\frac{\ddot{a}}{a}\)) L, la cual se observa como un estrés anómalo. Tomando\(\frac{\ddot{a}}{a} \sim H^{2}_{o}\), la aceleración anómala de un extremo del hueso con relación al otro es ∼ LH ². La compresión o tensión correspondiente es ∼ mLh ², donde m es tu masa corporal. La deformación resultante es\(\epsilon\) ∼\(\frac{mLH^{2}}{AE}\), donde E es el módulo de Young del hueso (aproximadamente 10 ¹⁰ Pa) y A es el área transversal del hueso.

Poniendo en números, el resultado para la cepa es de aproximadamente 10 ⁻⁴⁰, que es demasiado pequeño para ser medible por cualquier técnica imaginable, y en realidad estaría inundado por otros efectos. Dado que el signo de a¨ es actualmente positivo, esta deformación es de tracción, no compresiva. En la era anterior, dominada por la materia del universo, habría sido compresiva.

No hay una “tendencia secular”, es decir, el hueso de tu pierna no se está expandiendo con el tiempo. Está en equilibrio, y es simplemente alargada imperceptiblemente comparada con la longitud si hubiera tenido sin el efecto de expanson cosmológica.

Ejemplo 25: tensión en un núcleo atómico

La estimación en el ejemplo 24 también se puede aplicar a un núcleo atómico, que tiene un “módulo de Young” nuclear del orden de 1 MeV/fm ³ ∼ 10 ³² Pa. El resultado es una cepa\(\epsilon\) ∼ 10 ⁻⁵².

Ejemplo 26: una gran rasgadura

Se cree que las formas conocidas de materia tienen ecuaciones de estado P = w\(\rho\) con w ≥ −1. El valor para un universo dominado por vacío sería w = −1. Las observaciones cosmológicas ²³ muestran que empíricamente el universo actual se comporta como si estuviera hecho de cosas con w = −1.03 ± .16, y esto deja abierta la posibilidad de w < −1. En este caso, la solución a las ecuaciones de Friedmann da un factor de escala a (t) que sopla hasta el infinito en alguna t finita. En tal escenario, conocido como “Big Rip”,\((\frac{d}{dt})(\frac{\ddot{a}}{a})\) diverge, y cualquier sistema, por muy apretado que sea, es desgarrado. ²⁴

---

²³ Carnero et al., arxiv.org/abs/1104.5426

²⁴ Caldwell et al., arxiv.org/abs/astro-ph/0302506

Los ejemplos 24-26 muestran que excepto bajo hipotéticas condiciones cosmológicas extremas, no hay esperanza de detectar ningún efecto de expansión cosmológica en sistemas hechos de materia condensada. Necesitamos mirar sistemas mucho más grandes para ver cualquier efecto, y tales sistemas se mantienen unidos por la gravedad. Por concreción, sigamos hablando del sistema tierra-sol. No sólo es pequeña la fuerza anómala sobre la tierra, no se garantiza que produzca ninguna tendencia secular, que es la que más probablemente sería detectable. La dirección de la fuerza anómala sobre la tierra es hacia afuera para una expansión cosmológica acelerada, como ahora sabemos es el caso de la época actual. Como ejemplo en el que no se produce ninguna tendencia secular, una cosmología dominada por el vacío da un valor constante para\(\frac{\ddot{a}}{a}\), por lo que la fuerza exterior es constante. Al igual que con el efecto de la presión de radiación, la existencia de esta fuerza constante hacia afuera es casi equivalente a reescalar la fuerza gravitacional del sol en una pequeña cantidad, por lo que el movimiento sigue siendo casi kepleriano, pero con una constante ligeramente “incorrecta” de proporcionalidad en la ley de periodos de Kepler. La tasa de cambio\(\dot{r}\) en el radio de la órbita circular es, por lo tanto, cero en este caso.

Pero en la mayoría de las cosmologías no\(\frac{\ddot{a}}{a}\) es exactamente constante, y la fuerza anómala sobre la tierra varía. En una cosmología dominada por la materia con\(\Lambda\) = 0, en su fase de expansión, la fuerza es hacia adentro pero disminuyendo con el tiempo, por lo que la órbita se expande con el tiempo. Lo que realmente importa entonces, es\((\frac{d}{dt})(\frac{\ddot{a}}{a})\). Si fuéramos libres de elegir cualquier función para a (t), podríamos inventar ejemplos en los que\(\dot{a}\) > 0 pero\((\frac{d}{dt})(\frac{\ddot{a}}{a})\) < 0, para que el sistema solar respondiera a la expansión cosmológica ¡encogiéndose!

La función a (t), sin embargo, tiene que satisfacer las ecuaciones de Friedmann, una de las cuales es (en unidades con G ≠ 1)

\[\frac{\ddot{a}}{a} = G \Big[ \dfrac{1}{3} \Lambda - \frac{4 \pi}{3} (\rho + 3P) \Big] \ldotp \tag{8.2.18} \]

La época actual del universo parece estar bien modelada por la energía oscura descrita por un polvo constante\(\Lambda\) más con P <<\(\rho\). Diferenciar a ambos lados con respecto al tiempo da

\[\dfrac{d}{dt} \left(\dfrac{\ddot{a}}{a}\right) \propto \dot{\rho}, \tag{8.2.19} \]

con una constante negativa de proporcionalidad. Esto asegura que el signo del efecto sea siempre como se esperaba de la ingenua imagen maniquea de fuerzas vinculantes que luchan contra la expansión cosmológica (o quizás cooperando durante la fase de contracción de una cosmología Big Crunch).

Una forma de entender por qué esto se reduce tan bien a una dependencia de\(\dot{\rho}\) es el razonamiento dado en el ejemplo 15, en el que encontramos que la aceleración relativa de dos partículas de prueba A y B en una cosmología FRW dominada por la materia podría calcularse con precisión pretendiendo que se debía a la presencia del polvo en cualquier esfera S dada que rodea las dos partículas. Ahora dejamos que A sea el sol, B la tierra, y S una esfera centrada en el sol cuyo radio es igual al radio de la órbita circular de la tierra. Debido a la expansión cosmológica, el polvo dentro de S se adelgaza con el tiempo, reduciendo su densidad\(\rho\). La aplicación de las leyes de Newton a la órbita de la tierra da\(\omega^{2} r = \frac{GM}{r^{2}}\), y la conservación del momento angular da como resultado\(\omega\) r ² = const. Un cálculo da $$\ frac {r} {r_ {o}} =\ frac {M + (\ frac {4\ pi} {3})\ rho_ {o} r^ {3} _ {o}} {M + (\ frac {4\ pi} {3})\ rho r^ {3}}\ tag {8.2.20} $$, que resulta en\(\frac{\dot{r}}{r_{o}} \approx −(\frac{4 \pi}{3})G \omega^{−2}_{o} \dot{\rho}\). Aplicación de las ecuaciones de Friedmann

\[\frac{\dot{r}}{r_{o}} = \omega^{-2}_{o} \left(\dfrac{d}{dt}\right) \left(\frac{\ddot{a}}{a}\right), \tag{8.2.21} \]

que es válido generalmente, no sólo para P = 0. El\(\omega^{−2}_{o}\) factor muestra que el efecto es menor para sistemas más estrechamente unidos.

Sabemos que el universo en la época actual tiene\((\frac{d}{dt})(\frac{\ddot{a}}{a})\) > 0 porque\(\dot{\rho}\) < 0, y para propósitos de una estimación de orden de magnitud podemos tomar\((\frac{d}{dt})(\frac{\ddot{a}}{a}) \sim H^{3}_{o}\). Al enchufar números para el sistema tierra-sol, encontramos que desde la edad de los dinosaurios, el radio de la órbita terrestre ha crecido menos que el diámetro de un núcleo atómico. ²⁵

Nota

La pintoresca imagen proviene de Cooperstock et al., http://arxiv.org/abs/astro-ph/9803097v1, quienes dan un cálculo diferente que lleva a un resultado por\(\dot{r}\) exactamente equivalente al que aquí se deriva.

Observaciones

Históricamente, se creía que la constante cosmológica era cero, que casi toda la materia en el universo estaba en forma de átomos, y que por lo tanto solo había un parámetro cosmológico interesante para medir, que era la densidad promedio de la materia. Esta densidad era muy difícil de determinar, incluso dentro de un orden de magnitud, porque la mayor parte de la materia en el universo probablemente no emite luz, dificultando su detección. Las escalas de distancia astronómica también fueron muy mal calibradas contra unidades absolutas como la SI. A partir de 1995, sin embargo, un nuevo conjunto de técnicas condujo a una era de cosmología de alta precisión.

Curvatura espacial a partir de fluctuaciones CMB

Una fuerte restricción en los modelos proviene de mediciones precisas del fondo cósmico de microondas, especialmente por la sonda COBE 1989-1993, y su sucesora 2001-2009, la sonda de anisotropía de microondas Wilkinson, posicionada en el punto L2 Lagrange del sistema tierra-sol, más allá de la Tierra en la línea que conecta sol y tierra. ²⁶ La temperatura de la radiación cósmica de fondo de microondas no es la misma en todas las direcciones, y se puede medir en diferentes ángulos. En un universo con curvatura espacial negativa, la suma de los ángulos interiores de un triángulo es menor que el valor euclidiano de 180 grados. Por lo tanto, si observamos una variación en el CMB sobre algún ángulo, la distancia entre dos puntos en la superficie de la última dispersión es en realidad mayor de lo que se habría inferido de la geometría euclidiana. La escala de distancia de tales variaciones está limitada por la velocidad del sonido en el universo primitivo, por lo que se puede trabajar hacia atrás e inferir la curvatura espacial del universo basándose en la escala angular de las anisotropías. Las mediciones de curvatura espacial generalmente se establecen en términos del parámetro\(\Omega\), definido como la densidad promedio total de todos los términos fuente en las ecuaciones de campo de Einstein, dividida por la densidad crítica que da como resultado un universo plano. \(\Omega\)incluye contribuciones de la materia\(\Omega_{M}\), la constante cosmológica\(\Omega_{\Lambda}\), y la radiación (insignificante en el universo actual). Los resultados de WMAP, combinados con otros datos de otros métodos, dan\(\Omega\) = 1.005 ± .006. En otras palabras, el universo es casi espacialmente plano.

Figura\(\PageIndex{6}\) - La escala angular de fluctuaciones en el fondo cósmico de microondas puede utilizarse para inferir la curvatura del universo.

Aceleración de la expansión de datos de Supernova

Los datos de supernova descritos en la sección 8.2 complementan los datos CMB porque son principalmente sensibles a la diferencia\(\Omega_{\Lambda} − \Omega_{M}\), más que a su suma\(\Omega = \Omega_{\Lambda} + \Omega_{M}\). Esto se debe a que estos datos miden la aceleración o desaceleración de la expansión del universo. La materia produce desaceleración, mientras que la constante cosmológica da aceleración. La Figura 8.2.7 muestra algunos datos recientes de supernova. ²⁷ El eje horizontal da el factor de desplazamiento al rojo z =\(\frac{\lambda' − \lambda}{\lambda}\), donde\(\lambda'\) se encuentra la longitud de onda observada en la tierra y\(\lambda\) la longitud de onda emitida originalmente. Mide qué tan rápido está retrocediendo de nosotros la galaxia de la supernova. El eje vertical es\(\Delta\) (M−m) = (M−m) − (M−m) _vacío, donde m es la magnitud aparente, M es la magnitud absoluta y (m − M) _vacío es el valor esperado en un modelo de un universo vacío, con\(\Omega\) = 0. La diferencia M−m es una medida de distancia, por lo que esencialmente se trata de un gráfico de distancia versus velocidad recesional, del mismo tipo general utilizado por Hubble en su descubrimiento original de la expansión del universo. Restar (M−m) _vacío en el eje vertical hace que sea más fácil ver pequeñas diferencias. Dado que los datos WMAP requieren\(\Omega\) = 1, necesitamos ajustar los datos de supernova con valores de\(\Omega_{M}\) y\(\Omega_{\Lambda}\) que suman uno. Intentar hacerlo con\(\Omega_{M}\) = 1 y\(\Omega_{\Lambda}\) = 0 es claramente inconsistente con los datos, por lo que podemos concluir que la constante cosmológica es definitivamente positiva.

Figura\(\PageIndex{7}\) - Una gráfica de Hubble para supernovas distantes. Cada punto de datos representa un promedio sobre varias supernovas diferentes con casi la misma z.

Densidad de la materia de las oscilaciones acústicas bariónicas

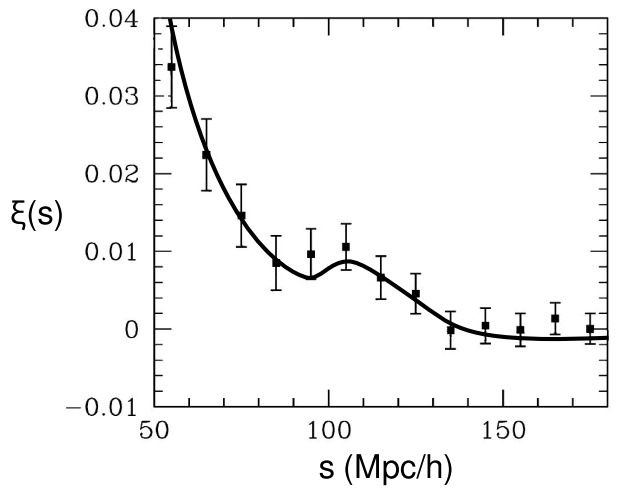
Esfuerzos como el Sloan Digital Sky Survey han realizado mapas tridimensionales de la densidad de la materia luminosa en el universo. ²⁸ La distribución es grumosa. Al medir la correlación promedio\(\xi\) entre la densidad en puntos separados por alguna distancia s (medida en el marco comoving), uno esperaría que la (s) función\(\xi\) (s) sería más grande cuando s era pequeña y simplemente se estrecharía con el aumento de s. Por analogía, no solemos encontrar un Manhattan paisaje de rascacielos al lado del otro con un desierto montañoso deshabitado. Por otro lado, imagínese construir tal función de correlación para casas en una subdivisión en la que las carreteras no formen ninguna rejilla regular, pero las regulaciones de zonificación prohíben la construcción de casas en lotes de menos de cierto tamaño. En esta situación, habría cero probabilidad de encontrar casas separadas por distancias muy pequeñas, y\(\xi\) (s) exhibirían un pico a alguna escala mayor establecida por el código legal. Los resultados reales de los estudios del cielo muestran tal pico, lo que se debe a la conocida física conocida como oscilaciones acústicas de bariones (BAO). ²⁹ En el universo primitivo, cualquier región de sobredensidad tendería a crear una onda sonora radiante como el estallido de un petardo. Tales ondas se propagaron a una velocidad conocida (aproximadamente la mitad de la velocidad de la luz) durante un tiempo conocido (alrededor de 400,000 años, hasta que la materia se desionizó y se volvió transparente a la radiación, haciéndola inmune a la presión fotónica que impulsó las oscilaciones). Esto conduce a una distancia conocida s, que forma una regla estándar en la que se produce el pico en\(\xi\) (s). En los modelos cosmológicos, estos resultados limitan fuertemente\(\Omega_{M}\), a la vez que son relativamente insensibles\(\Omega_{\Lambda}\), y por lo tanto son complementarios tanto a los datos de supernova como a los resultados de CMB.

Figura\(\PageIndex{8}\) - El pico acústico en la función de correlación BAO. Redibujado de Eisenstein, New Astronomy Reviews. 49 (2005) 360, tal como se reproduce en Bassett y Hlozek, 2009, arxiv.org/abs/0910.5224.

Conclusiones sobre Cosmología

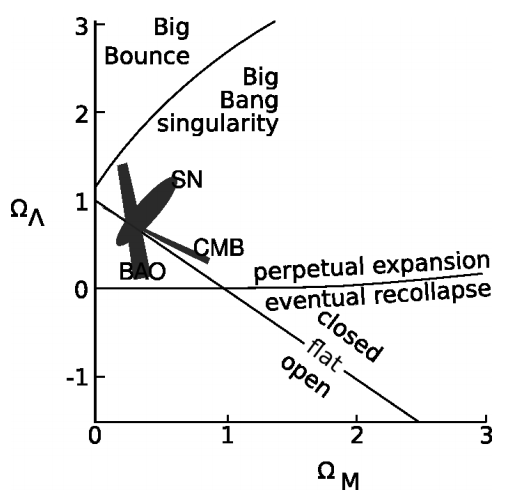
La Figura 8.2.9 resume lo que podemos concluir sobre nuestro universo, parametrizado en términos de un modelo con ambos\(\Omega_{M}\) y\(\Omega_{\Lambda}\) distinto de cero. ³⁰ Podemos decir que se originó en una singularidad del Big Bang, que seguirá expandiéndose para siempre, y que es casi plano. Obsérvese que en una cosmología con valores distintos de cero para ambos\(\Omega_{M}\) y\(\Omega_{\Lambda}\), no existe una vinculación estricta entre la curvatura espacial y la cuestión del recolapso, ya que hay en un modelo con solo materia y sin constante cosmológica; por lo tanto, aunque sabemos que el universo no se volverá a colapsar, nosotros no se sabe si su curvatura espacial es ligeramente positiva (cerrada) o negativa (abierta).

Figura\(\PageIndex{9}\) - Los parámetros cosmológicos de nuestro universo, después de Perlmutter, 1998, arxiv.org/abs/astro-ph/9812133 y Kowalski, 2008, arxiv.org/abs/0804.4142. Las tres regiones sombreadas representan las regiones de confianza del 95% para los tres tipos de observaciones.

Comprobaciones de consistencia

Las consideraciones astrofísicas proporcionan más restricciones y verificaciones de consistencia. En la era anterior al advenimiento de la cosmología de alta precisión, las estimaciones de la edad del universo oscilaban entre 10 mil millones y 20 mil millones de años, y el extremo inferior era inconsistente con la edad de los cúmulos globulares más antiguos. Se creía que esto era un problema ya sea para la cosmología observacional o para los modelos astrofísicos utilizados para estimar la edad de los racimos: “No puedes ser mayor que tu ma”. Los datos actuales han demostrado que las bajas estimaciones de la edad fueron incorrectas, por lo que se restablece la consistencia.

Que solo una pequeña fracción de la materia del universo era luminosa había sido sospechada por astrónomos como Zwicky ya en 1933, basándose en la incapacidad de conciliar la cinemática observada con las leyes de Newton si se suponía que toda la materia era luminosa.

Materia Oscura

Otra restricción proviene de modelos de nucleosíntesis durante la época poco después del Big Bang (antes de la formación de las primeras estrellas). Las abundancias relativas observadas de hidrógeno, helio y deuterio no pueden conciliarse con la densidad de “polvo” (es decir, materia no relativista) inferida de los datos observacionales. Si la densidad de masa inferida se debía enteramente a la materia “bariónica” normal (es decir, la materia cuya masa consistía principalmente en protones y neutrones), entonces las reacciones nucleares en el denso universo temprano deberían haber procedido de manera relativamente eficiente, conduciendo a una relación mucho mayor de helio a hidrógeno, y una proporción mucho más baja de helio a hidrógeno, y mucho menor abundancia de deuterio. La conclusión es que la mayor parte de la materia en el universo debe estar hecha de un tipo desconocido de materia exótica no bariónica, conocida genéricamente como “materia oscura”.

También se requiere la existencia de materia no bariónica para conciliar la densidad observada de galaxias con la fuerza observada de las fluctuaciones del CMB, y en la fusión de cúmulos de galaxias se ha observado que el potencial gravitacional se compensa con respecto al plasma radiante. Un artículo de revisión de 2012 sobre materia oscura es Roos, arxiv.org/abs/1208.3662.

Se están llevando a cabo diversos experimentos para detectar directamente la materia oscura. A partir de 2013, el experimento más sensible ha dado resultados nulos: arxiv.org/abs/1310.8214.

En un momento se esperaba ampliamente que la materia oscura consistiera en la partícula supersimétrica más ligera, que podría ser por ejemplo el neutralino. Sin embargo, los resultados del LHC parecen hacer poco probable que nuestro universo exhiba supersimetría, asumiendo que la escala de energía es la escala electrodébil, que es la única escala que tiene una fuerte motivación. Ahora parece más probable que la materia oscura consista en alguna otra partícula como neutrinos estériles o axiones. Incluso con la inclusión de la materia oscura, existe un problema con la abundancia de litio-7 en relación con el hidrógeno, que los modelos sobrepredicen en gran medida. ³¹

Referencias

²⁶ Komatsu et al., 2010, arxiv.org/abs/1001.4538

²⁷ Riess et al., 2007, arxiv.org/abs/astro-ph/0611572. Un conjunto de datos más grande se analiza en Kowalski et al., 2008, arxiv.org/abs/0804.4142.

²⁸ Sánchez et al., 2012, arxiv.org/abs/1203.6616

²⁹ Bassett y Hlozek, 2009, arxiv.org/abs/0910.5224

³⁰ Véase Carroll, “La constante cosmológica”, http://www.livingreviews.org/lrr-2001-1 para un tratamiento matemático completo de este tipo de modelos.

³¹ arxiv.org/abs/0808.2818, arxiv.org/abs/1107.1117