2.3: Algún razonamiento dimensional y sus consecuencias

Obtención de las dimensiones correctas

Como toda ecuación físicamente correcta, la Ecuación 2.2.1 debe representar la igualdad no sólo de magnitudes sino también de dimensiones. En la mayoría de los sistemas mecánicos se necesitan tres dimensiones básicas para expresar fuerzas, movimientos y propiedades del sistema; estas generalmente se toman como masa (\(\mathrm{M}\)), longitud (\(\mathrm{L}\)) y tiempo (\(\mathrm{T}\)). Entonces, cualquiera que sea la forma del término o términos del lado derecho de la Ecuación 2.2.1\(U\), las variables\(D\)\(\rho\),,, y\(\mu\) deben combinarse de tal manera que cada término tenga las dimensiones de fuerza, porque el lado izquierdo tiene las dimensiones de fuerza. La siguiente lista da las dimensiones de cada una de las cinco variables involucradas en el flujo más allá de una esfera, en términos de masa\(\mathrm{M}\)\(\mathrm{L}\), longitud y tiempo\(\mathrm{T}\):

\(\begin{array}{ll}{F_{D}} & {-\quad \mathrm{ML} / \mathrm{T}^{2}} \\ {U} & {-\quad\mathrm{L} / \mathrm{T}} \\ {D} & {-\quad\mathrm{L}} \\ {\rho} & {-\quad\mathrm{M} / \mathrm{L}^{3}} \\ {\mu} & {-\quad\mathrm{M} / \mathrm{LT}}\end{array}\)

La única variable aquí cuyas dimensiones no son directas es\(\mu\); las dimensiones\(\mathrm{M} / \mathrm{L} \mathrm{T}\) se obtienen mediante el uso de la Ecuación 1.3.6, por la cual\(\mu\) se define.

Es ventajoso reescribir ecuaciones como la Ecuación 2.2.1 en forma adimensional. Para ello, primero hacer que el lado izquierdo sea adimensional dividiendo\(F_{D}\) por algún producto de variables independientes que a su vez tenga las dimensiones de fuerza. Usando la lista de dimensiones anterior, puede verificar que\(\rho U^{2} D^{2}\) tiene las dimensiones de fuerza:

\(\rho U^{2} D^{2}: \left(\mathrm{M} / \mathrm{L}^{3}\right)(\mathrm{L} / \mathrm{T})^{2}(\mathrm{L})^{2}=\mathrm{ML} / \mathrm{T}^{2}\)

Entonces, dividir el lado izquierdo de la Ecuación 2.2.1 por\(\rho U^{2} D^{2}\) hace que el lado izquierdo de la ecuación sea adimensional. El resultado,\(F_{D} / \rho U^{2} D^{2}\), puede verse como una forma adimensional de\(F_{D}\). Eso deja que el lado derecho de la Ecuación 2.2.1 se haga adimensional. Hay una y única manera las cuatro variables\(U\),,\(D\)\(\rho\), y se\(\mu\) pueden combinar en una variable adimensional, a saber\(\rho U D / \mu\):

\(\rho U D / \mu\):\(\left(\mathrm{M} / \mathrm{L}^{3}\right)(\mathrm{L} / \mathrm{T})(\mathrm{L}) /(\mathrm{M} / \mathrm{LT})\)... \(\mathrm{M}\),\(\mathrm{L}\),\(\mathrm{T}\) cancelar

(Esa afirmación no es estrictamente cierta, pero todas las demás posibilidades simplemente se\(\rho U D / \mu\) elevan a algún poder, y no son independientes de ellas)\(\rho U D / \mu\). Entonces, cualquiera que sea la forma de la función\(f\), el lado derecho de la forma adimensional de la Ecuación 2.2.1 se puede escribir usando solo una variable adimensional:

\[\frac{F_{D}}{\rho U^{2} D^{2}}=f\left(\frac{\rho U D}{\mu}\right) \label{dimensionless} \]

Una función simplificada

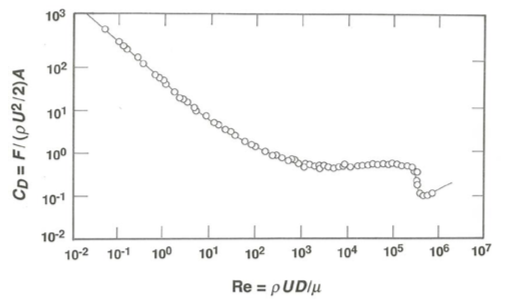
La ecuación\ ref {adimensional} es una forma equivalente pero adimensional de la Ecuación 2.2.1. La gran ventaja de la ecuación adimensional es que involucra solo dos variables, una variable adimensional dependiente\(F_{D} / \rho U^{2} D^{2}\) y una variable adimensional independiente,\(\rho U D / \mu\) en lugar de las cinco originales. Piense en el enorme ahorro en esfuerzo que esto implica para un programa experimental para caracterizar la fuerza de arrastre. Si tuvieras que medir\(F_{D}\) en función de cada una de las cuatro variables manteniendo constantes las otras tres, generarías montañas de datos y gráficas. Pero la Ecuación\ ref {adimensional} te dice que\(U\)\(D\)\(\rho\),,, y solo\(\mu\) necesita ser variada para hacer\(\rho U D / \mu\) variar. Todos los puntos experimentales\(F_{D} / \rho U^{2} D^{2}\) obtenidos variando\(\rho U D / \mu\) deben graficarse como una curva en una gráfica bidimensional con estas dos variables a lo largo de los ejes. Cualesquiera que sean los valores de\(U\)\(D\)\(\rho\),\(\mu\), y, todas las posibles realizaciones del flujo pasado una esfera se expresan por una sola curva. Esta curva se muestra en la Figura\(\PageIndex{1}\) junto con algunos de los puntos experimentales que se han utilizado para definirla. La física detrás de la curva se discute en el Capítulo 3, después de más antecedentes en los principios de la dinámica de fluidos. Y podrías encontrar la curva variando solo una de las cuatro variables\(U\),\(D\),\(\rho\), y\(\mu\) —aunque es posible que no puedas obtener un rango muy amplio de valores de\(\rho U D / \mu\) variando solo una de esas variables. Un número bastante pequeño de experimentos que involucran valores de las variables independientes originales que se combinaron para abarcar un amplio rango de\(\rho U D / \mu\) serían suficientes para caracterizar todas las demás combinaciones posibles de variables independientes. Esto se debe a que cada punto de la gráfica adimensional representa muchas combinaciones posibles diferentes de las variables originales, una infinidad de estas, de hecho. Así, obtienes una capacidad predictiva de largo alcance sobre la base de un esfuerzo de observación relativamente pequeño.

Figura\(\PageIndex{1}\): Gráfica de fuerza de arrastre adimensional vs. número de Reynolds para el flujo de un fluido viscoso más allá de una esfera. La fuerza de arrastre adimensional se expresa en forma de un coeficiente de arrastre definido convencionalmente más que como la fuerza de arrastre adimensional\(F_{D}\); ver más adelante en el texto. Los puntos experimentales son de varias fuentes, y son algo generalizados. Algunos de los puntos de datos provienen de la sedimentación de una esfera a través de un quieto fluido, y otros son del flujo más allá de una esfera mantenida en reposo. Para una trama más detallada, véase, por ejemplo, Schiller (1932).

Un escéptico podría encontrar que todo esto es demasiado bueno para ser verdad. Pero el caso es que así funcionan las cosas, y el análisis del flujo pasado una esfera es solo un buen ejemplo. Sin embargo, está en regla una nota de precaución. Es prudente variar la mayor cantidad de variables en un rango lo más amplio posible; esto no requiere un enorme número de observaciones, y es una comprobación de la exactitud de su análisis. A continuación verá con más detalle que si hay un mayor número de variables importantes de lo que piensa, sus puntos de datos formarían una banda dispersa en lugar de una sola curva. Entonces, si variabas solo una variable para tratar de encontrar la curva, de hecho obtendrías una curva, pero no sería la curva que buscabas; te faltaría la dispersión que se manifestaría si variaras también las otras variables.

Varias notas

Primero, las variables de la forma\(\rho U D / \mu\) se llaman números de Reynolds, generalmente denotados por\(\mathrm{Re}\). Siempre que tanto la densidad como la viscosidad son importantes en un problema y se involucra tanto una variable de longitud como una velocidad, se puede formar y usar un número de Reynolds. Por lo tanto, hay muchos números diferentes de Reynolds, con diferentes variables de longitud y velocidad dependiendo del problema particular. Encontrarás a otros en capítulos posteriores.

Segundo, para el flujo constante hemos asumido, las variables\(U\),\(D\)\(\rho\), y\(\mu\) caracterizan no solo todo sobre las distribuciones de esfuerzo cortante y presión sobre toda la superficie de la esfera, que suman\(F_{D}\), sino también las distribuciones de esfuerzo cortante, presión y velocidad del fluido en cada punto del fluido circundante. Porque\(\rho U D / \mu\) reemplaza estas cuatro variables en el lado derecho de la Ecuación\ ref {adimensional}, lo mismo puede decirse del número de Reynolds. Cualquier cosa sobre fuerzas y movimientos que desee considerar puede verse como especificada completamente por el número de Reynolds.

Tercero, hay otra consecuencia importante del hecho de que cada punto en la curva de\(F_{D} / \rho U^{2} D^{2}\) vs.\(\rho U D / \mu\) representa una infinidad de combinaciones de\(U\),\(D\),\(\rho\), y\(\mu\). Supongamos que querías encontrar la fuerza de arrastre que ejerce un cierto flujo sobre una esfera que es demasiado grande para caber en tu laboratorio o tu sótano. Se podría trabajar con una esfera mucho más pequeña ajustando los valores de\(U\),\(\rho\), y\(\mu\) así que eso\(\rho U D / \mu\) es lo mismo que en el flujo en cuestión más allá de la esfera grande (Figura\(\PageIndex{2}\)). Entonces a partir de la curva en Figura\(\PageIndex{1}\) el valor de\(F_{D} / \rho U^{2} D^{2}\) es también el mismo, y a partir de ella se puede encontrar la fuerza de arrastre\(F_{D}\) sobre la esfera grande sustituyendo los valores correspondientes de\(U\),\(D\), y\(\rho\). O, por otro lado, se podría estudiar el flujo alrededor de una esfera muy pequeña mediante el uso de una esfera mucho más grande, con la misma total confianza en los resultados (Figura\(\PageIndex{2}\)). Esta es la esencia del modelado a escala: el estudio de un sistema físico mediante el uso de otro a una escala física menor o mayor pero con variables ajustadas para que todas las fuerzas y movimientos en los dos sistemas estén en las mismas proporciones. La figura\(\PageIndex{2}\) muestra cómo podrías usar el flujo alrededor de una esfera pequeña con diámetro\(D_{m}\) para modelar el flujo alrededor de una esfera mucho más grande con diámetro\(D_{o}\). Tendrías que ajustar las velocidades de flujo\(U_{m}\) y\(U_{o}\), así como las viscosidades del fluido\(\mu_{m}\) y\(\mu_{o}\) y las densidades del fluido\(\rho_{m}\) y\(\rho_{o}\), para que el número de Reynolds\(\mathrm{Re}_{m}\), igual a\(\rho_{m} U_{m} D_{m} / \mu_{m}\), en el modelo sea el mismo que el número de Reynolds \(\mathrm{Re}_{o}\), igual a\(\rho_{o} U_{o} D_{o} / \mu_{o}\), en el flujo a gran escala. Entonces todas las fuerzas y movimientos están en la misma proporción en los dos flujos, y, específicamente, la fuerza de arrastre adimensional, o el coeficiente de arrastre, es el mismo en los dos flujos. A pesar de la gran diferencia en la escala física, ambos flujos están representados por el mismo punto en la gráfica de coeficiente de arrastre vs. número de Reynolds, por lo que cualquier cosa sobre los dos flujos, siempre que se exprese en forma adimensional, es lo mismo en los dos flujos. Cada punto en la curva de\(F_{D} / \rho U^{2} D^{2}\) vs.\(\rho U D / \mu\) representa un número infinito de experimentos posibles, ¡cada uno de los cuales es un modelo a escala de todos los demás!

Figura\(\PageIndex{2}\): Un ejemplo de modelado a escala: usando flujos alrededor de una pequeña esfera para modelar el flujo alrededor de una esfera grande. (Se supone que el objeto en la parte inferior derecha es la punta del dedo de alguien).

Cuarto, en\(\PageIndex{1}\) la Figura la fuerza de arrastre adimensional se escribe en una forma convencional que es ligeramente diferente a la derivada anteriormente:\(F_{D} /\left(\rho U^{2} / 2\right) A\), donde\(A\) es el área transversal de la esfera, igual a\(\pi D^{2} / 4\). Esto difiere de\(F_{D} / \rho U^{2} D^{2}\) por el factor\(\pi / 8\), pero sus dimensiones son exactamente las mismas. Por lo general se le llama coeficiente de arrastre, denotado por\(C_{D}\); se puede ver por qué ese término surgió escribiendo

\[F_{D}=C_{D} \frac{\rho U^{2}}{2} A \label{2.3} \]

donde el factor del\(\left(\rho U^{2} / 2\right) A\) lado derecho tiene dimensiones de fuerza. La relación funcional entre la fuerza de arrastre adimensional y el número de Reynolds en la ecuación\ ref {adimensional} se puede escribir en una forma completamente equivalente usando\(C_{D}\):

\[C_{D}=\frac{F D}{\frac{\rho U^{2}}{2} A}=f\left(\frac{\rho U D}{\mu}\right) \label{2.4} \]

Quinto, existen versiones alternativas de la variable adimensional dependiente. Dividir por no\(\rho U^{2} D^{2}\) es la única manera de no dimensionalizar\(F_{D}\). Puedes comprobar por ti mismo eso\(F_{D} / \mu U D\),\(\rho F_{D} / \mu^{2}\), y\(F_{D} / \mu U\) son otras posibilidades, obtenidas combinando\(F_{D}\) con las cuatro variables\(\rho\),\(\mu\),\(U\), y\(D\) tomadas tres a la vez. (Verá en la siguiente sección cómo derivar tales variables.) En ocasiones, como en los dos últimos casos, una de las variables cae; esto ocurre cuando\(\mathrm{M}\) o\(\mathrm{L}\) o\(\mathrm{T}\) aparece en sólo una de las cuatro variables elegidas. Cualquiera de estas tres variables adimensionales dependientes alternativas serviría tan bien como\(F_{D} / \rho U^{2} D^{2}\) para representar los datos. Verás a continuación, sin embargo, que a veces uno es más revelador que los demás.